最大权闭合子图
参考博客:https://www.cnblogs.com/dilthey/p/7565206.html
什么是最大权闭合子图?
给你一个图(数字表示点权)
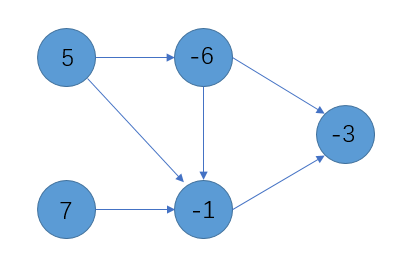
让你在其中选点(选了就要跟着选它连向的点),使得权值最大,问选法。
如图最大权闭合子图为 7 => -1 => -3
如何求解?
我们可以用最小割求解。
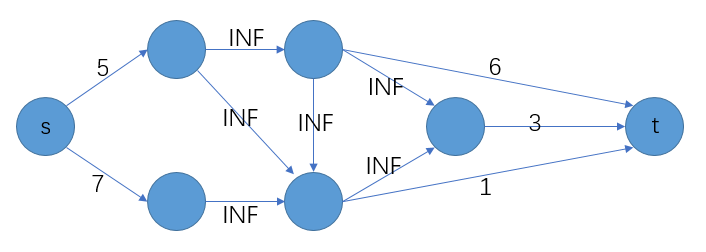
我们把 S 向正权点连一条容量为权值的边,把负权点连一条容量为权值绝对值的边。
同时把原图的边权改为 INF,求最小割,如下图。
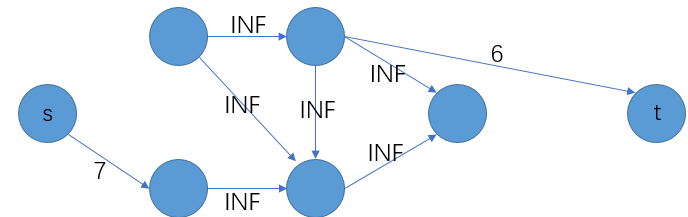
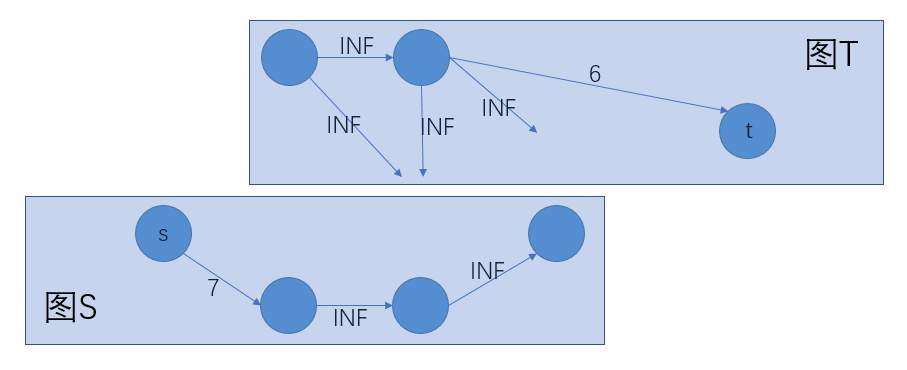
因为INF的边不会被割掉,很容易发现,S图是一个闭合子图,由于割掉的边的和是最小的,所以把代表正的点的边不选,代表负的点的边选,就是最优的选法。
综上所述,最大权闭合子图就是 S图,最大值就是 “正权点和-最小割”
模板题:[NOI2009]植物大战僵尸
题目描述
Plants vs. Zombies(PVZ)是最近十分风靡的一款小游戏。Plants(植物)和Zombies(僵尸)是游戏的主角,其中Plants防守,而Zombies进攻。该款游戏包含多种不同的挑战系列,比如Protect Your Brain、Bowling等等。其中最为经典的,莫过于玩家通过控制Plants来防守Zombies的进攻,或者相反地由玩家通过控制Zombies对Plants发起进攻。
现在,我们将要考虑的问题是游戏中Zombies对Plants的进攻,请注意,本题中规则与实际游戏有所不同。游戏中有两种角色,Plants和Zombies,每个Plant有一个攻击位置集合,它可以对这些位置进行保护;而Zombie进攻植物的方式是走到植物所在的位置上并将其吃掉。
游戏的地图可以抽象为一个N行M列的矩阵,行从上到下用0到N–1编号,列从左到右用0到M–1编号;在地图的每个位置上都放有一个Plant,为简单起见,我们把位于第r行第c列的植物记为Pr, c。
Plants分很多种,有攻击类、防守类和经济类等等。为了简单的描述每个Plant,定义Score和Attack如下:
Score[Pr, c]
Zombie击溃植物Pr, c可获得的能源。若Score[Pr, c]为非负整数,则表示击溃植物Pr, c可获得能源Score[Pr, c],若为负数表示击溃Pr, c需要付出能源 -Score[Pr, c]。
Attack[Pr, c]
植物Pr, c能够对Zombie进行攻击的位置集合。
Zombies必须从地图的右侧进入,且只能沿着水平方向进行移动。Zombies攻击植物的唯一方式就是走到该植物所在的位置并将植物吃掉。因此Zombies的进攻总是从地图的右侧开始。也就是说,对于第r行的进攻,Zombies必须首先攻击Pr, M-1;若需要对Pr, c(0≤c<M-1)攻击,必须将Pr,M-1, Pr, M-2 … Pr, c+1先击溃,并移动到位置(r, c)才可进行攻击。
在本题的设定中,Plants的攻击力是无穷大的,一旦Zombie进入某个Plant的攻击位置,该Zombie会被瞬间消灭,而该Zombie没有时间进行任何攻击操作。因此,即便Zombie进入了一个Plant所在的位置,但该位置属于其他植物的攻击位置集合,则Zombie会被瞬间消灭而所在位置的植物则安然无恙(在我们的设定中,Plant的攻击位置不包含自身所在位置,否则你就不可能击溃它了)。
Zombies的目标是对Plants的阵地发起进攻并获得最大的能源收入。每一次,你可以选择一个可进攻的植物进行攻击。本题的目标为,制定一套Zombies的进攻方案,选择进攻哪些植物以及进攻的顺序,从而获得最大的能源收入。
输入输出格式
输入格式:
输入文件pvz.in的第一行包含两个整数N, M,分别表示地图的行数和列数。
接下来N×M行描述每个位置上植物的信息。第r×M + c + 1行按照如下格式给出植物Pr, c的信息:第一个整数为Score[Pr, c], 第二个整数为集合Attack[Pr, c]中的位置个数w,接下来w个位置信息(r’, c’),表示Pr, c可以攻击位置第r’ 行第c’ 列。
输出格式:
输出文件pvz.out仅包含一个整数,表示可以获得的最大能源收入。注意,你也可以选择不进行任何攻击,这样能源收入为0。
#include<iostream>
#include<queue>
#include<cstring>
#include<cstdio>
using namespace std;
bool vis[1005];
int n,m,tot,cnt,sum,h[1005],H[1005];
int id[50][50],val[1005],deg[1005];
int deth[1005],cur[1005],S,T;
struct Protect{
int x,next;
}p[500005];
struct Edge{
int x,cap,next;
}e[500005];
inline void add_protect(int x,int y){
p[++tot].x=y,deg[y]++;
p[tot].next=H[x],H[x]=tot;
}
inline void add_edge(int x,int y,int z){
e[++tot].x=y,e[tot].cap=z;
e[tot].next=h[x],h[x]=tot;
e[++tot].x=x,e[tot].cap=0;
e[tot].next=h[y],h[y]=tot;
}
bool bfs(){
queue<int> q;
memset(deth,-1,sizeof(deth));
deth[S]=0,q.push(S),cur[S]=h[S];
while(!q.empty()){
int x=q.front();q.pop();
for(int i=h[x];i;i=e[i].next){
if(!e[i].cap||~deth[e[i].x])continue;
deth[e[i].x]=deth[x]+1;
cur[e[i].x]=h[e[i].x];
q.push(e[i].x);
if(e[i].x==T)return true;
}
}
return false;
}
int dfs(int x,int flow){
if(x==T)return flow;
for(int &i=cur[x];i;i=e[i].next)
if(e[i].cap&&deth[e[i].x]==deth[x]+1){
int sum=dfs(e[i].x,min(flow,e[i].cap));
if(sum>0){
e[i].cap-=sum,e[i^1].cap+=sum;
return sum;
}
}
return 0;
}
int dinic(){
int ans=0,k;
while(bfs())
while(k=dfs(S,1e9))ans+=k;
return ans;
}
void top_sort(){
queue<int> q;
for(int i=1;i<=cnt;i++)
if(!deg[i])vis[i]=true,q.push(i);
while(!q.empty()){
int x=q.front();q.pop();
for(int i=H[x];i;i=p[i].next){
deg[p[i].x]--;
if(!deg[p[i].x]){
vis[p[i].x]=true;
q.push(p[i].x);
}
}
}
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)id[i][j]=++cnt;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++){
int w,x,y;
scanf("%d",val+id[i][j]);
if(j<m)add_protect(id[i][j+1],id[i][j]);
scanf("%d",&w);
for(int k=1;k<=w;k++){
scanf("%d%d",&x,&y);
x++,y++;
add_protect(id[i][j],id[x][y]);
}
}
top_sort();
tot=1,S=0,T=cnt+1,sum=0;
for(int x=1;x<=cnt;x++){
if(!vis[x])continue;
if(val[x]>0)sum+=val[x];
for(int i=H[x];i;i=p[i].next)
if(vis[p[i].x]){
add_edge(p[i].x,x,1e9);
}
if(val[x]>0)add_edge(S,x,val[x]);
else add_edge(x,T,-val[x]);
}
printf("%d",sum-dinic());
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号