BSGS算法 （小步大步 Baby Step Gaint Step）
当你要求满足：
$$ A^x \equiv B \ (\bmod \ P) $$
的最小非负整数 x （gcd(A,P)==1）就可以用到 BSGS 了
设 $ m=\sqrt{P} $ 向上取整
处理一下那个式子：
$$ A^{i \times m-j} \equiv B \ (\bmod \ P) $$
$$ A^{i \times m} \equiv B \times A^j \ (\bmod \ P) $$
枚举 j（0到m），将 B*A^j 存入hash表里面
枚举 i（1到m），从hash表中找第一个满足上面这条式子的 j
x=i*m-j 即为所求 （感性理解）
模板题： 【xsy 1754】 离散对数
Description
给定B,N,P，求最小的满足B^L=N(mod P)的非负正数L。保证gcd(B,P)=1。
Input
多组数据，每行三个空格隔开的整数P,B,N。
Output
对于每组数据，输出答案。如无解，则输出"no solution"
CODE：
1 #include<iostream> 2 #include<cmath> 3 #include<cstdio> 4 #include<unordered_map> 5 using namespace std; 6 7 int p,a,b; 8 9 int qpow(int x,int y){ 10 int ans=1; 11 while(y){ 12 if(y&1)ans=1LL*ans*x%p; 13 y>>=1,x=1LL*x*x%p; 14 } 15 return ans; 16 } 17 18 int BSGS(){ 19 unordered_map<int,int> mp; 20 int m=ceil(sqrt(p)),tmp; 21 tmp=b; 22 for(int j=0;j<=m;j++) 23 mp[tmp]=j,tmp=1LL*tmp*a%p; 24 tmp=a=qpow(a,m); 25 for(int i=1;i<=m;i++){ 26 if(mp.count(tmp)) 27 return i*m-mp[tmp]; 28 tmp=1LL*tmp*a%p; 29 } 30 return -1; 31 } 32 33 int main(){ 34 while(~scanf("%d%d%d",&p,&a,&b)){ 35 int ans=BSGS(); 36 if(~ans)printf("%d\n",ans); 37 else printf("no solution\n"); 38 } 39 }
证明：
有这样一条式子：
证明了这个就搞定了
处理一下这个式子：
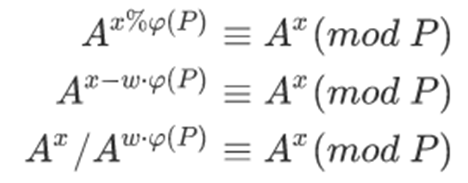
手头上的条件：gcd(A,P)=1
欧拉定理：
证完了OvO
