Lucas 卢卡斯定理
Lucas:
卢卡斯定理说白了只有一条性质
$$ C^n_m \equiv C^{n/p}_{m/p} \times C^{n \bmod p}_{m \bmod p} \ (mod \ \ p) $$
用于 m,n 很大时快速求组合数。(p 为质数)
CODE:
1 long long Lucas(long long n,long long m){ 2 if(m==0)return 1; 3 if(n<m)return 0; 4 if(n<p&&m<p)return fac[n]*inv[n-m]%p*inv[m]%p; 5 return Lucas(n/p,m/p)*Lucas(n%p,m%p)%p; 6 }
证明:
前置技能:二项式定理
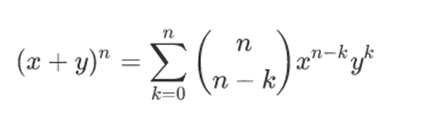
对于任意质数p,根据费马小定理有:
![]()
然后我们把(1+x)^n这个式子处理一下:
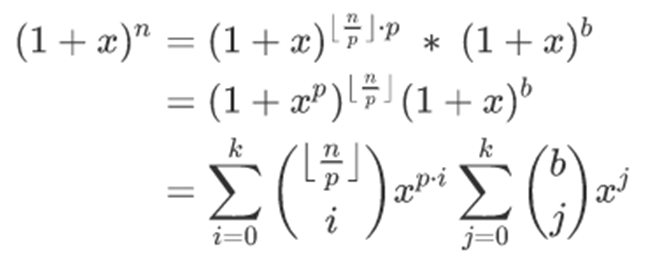
然后同时我们还有:
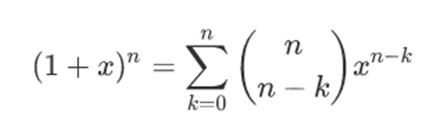
观察一下两个式子x的m次方的系数,可以得到:
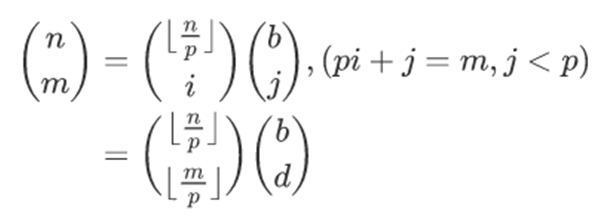
然后我们回到最开始的递归形式的那个式子,会发现…… 就证完了OvO
( 引用自 hy 大佬课件)


