题解P7108【移花接木】

Part1. 题目来源

【LGR-080】洛谷 11 月月赛 II div.2 C P7108 移花接木

Part2. 题解

23pts解法

对于前四档分数：

• Subtask #1 (3 points)：\(h=0\)。
• Subtask #2 (4 points)：\(a=b\)。
• Subtask #3 (8 points)：\(a=1\)。
• Subtask #4 (8 points)：\(b=1\)。

我们可以直接推出结论：

设灵树最初的形态为 \(A\)，转换后的形态为 \(B\)。

Subtask #1:

当 \(h=0\) 时，我们只需要将根节点所有的叶子都删除（移花）就可以了，答案即为 \(a\)。

Subtask #2:

当 \(a=b\) 时，我们只需要将叶子节点的儿子全部删除（移花）就可以了，答案即为叶子结点的个数 \(a^h\) 再乘上其儿子个数 \(a\)，答案即为 \(a^{h+1}\)

Subtask #3:

当 \(a=1\) 时，我们对于 \(B\) 的每个叶子节点，只需要一次接木操作即可通过移动加入该叶子节点到其某个祖先的边，因为需要加入 \(b^h-1\) 个点，因此需要进行 \(b^h-1\) 次移动（接木）操作，又因为最后还要删除多出的一个叶子节点，所以最终答案为 \(b^h\)

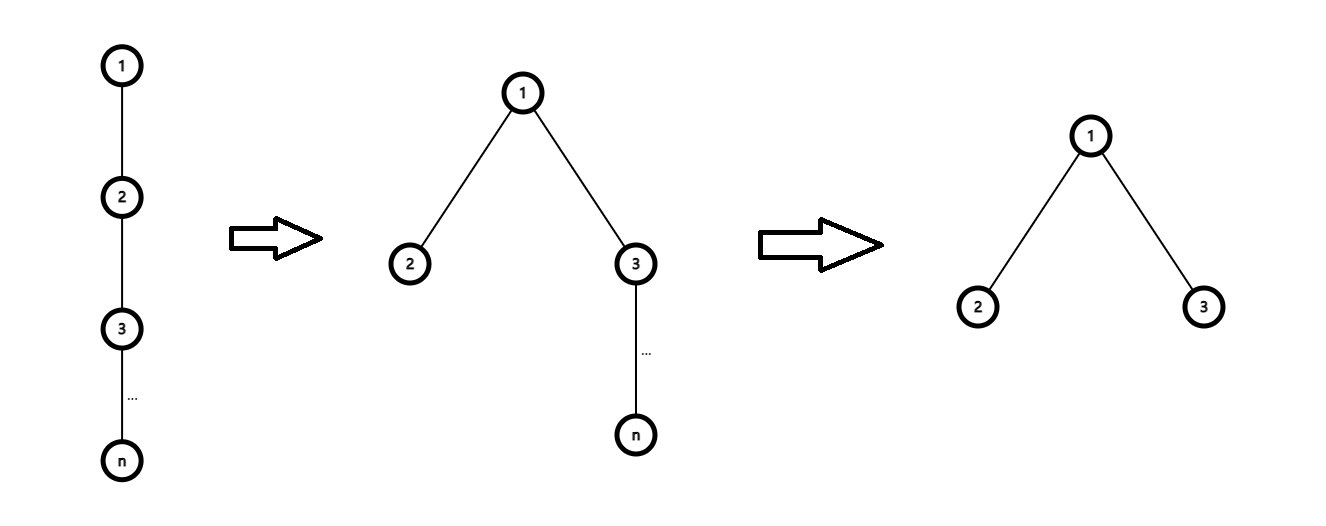
Subtask #4:

当 \(b=1\) 时，我们对于 \(A\) 中多余的节点需要全部删除，因此，在每一层中，我们都要删除 \(a-1\) 个节点，使得该层最后只有一个节点，因为有 \(h\) 层，所以要删除 \((a-1) \times h\) 个点，又因为叶子节点需要删除 \(a\) 个儿子节点，因此答案为 \((a-1) \times h+1\)

100pts解法：

分类讨论

当 \(a \ge b\) 时

对于第 \(i\) 层，因为上一层删除完后只剩下 \(b^{i-2}\) 个节点，所以需要删除 \(b^{i-2} \times b=b^{i-1}\) 个节点的多余儿子，而一个节点的多余的儿子有 \(a-b\) 个，因此一共要删除 \((a-b) \times (b^0+b^1+\dots+b^{h-1})\)，化简后即为 \((a-b) \times \frac{b^h-1}{b-1}\)，可以使用快速幂在 \(O(logn)\) 求解，又因为对于 \(b^h\) 个子节点每个都要删除 \(a\) 个儿子，因此一共要删除 \((a-b) \times \frac{b^h-1}{b-1}+b^h \times a\) 个节点

tips:当 \(b-1=0\) 即 \(b=1\) 时 \(\frac{b^h-1}{b-1}\) 无法通过逆元求解，因此可以直接推导出 \(b^0+b^1+\dots+b^{h-1}=1^0+1^1+\dots+1^{h-1}=h\)，也可以使用Subtask #4求解

当 \(a<b\) 时

对于第 \(i\) 层，因为上一层移动完后有 \(b\) 个节点，所以需要再移动 \(b^{i-1} \times (b-a)\) 个节点的作为上一层的儿子，因此一共要移动 \((b-a) \times \frac{b^h-1}{b-1}\) 个节点，与上一种情况基本相同，又因为对于 \(b^h\) 个子节点每个都要删除 \(a\) 个儿子，因此还要删除 \(b^h \times a\) 个节点，但又因为我们再刚才移动节点时可以移动要删除的节点减少移动次数，因此删除的节点个数还要减去移动的节点次数，因此设移动的节点次数 \(k=(b-a) \times \frac{b^h-1}{b-1}\)，答案即为 \(k+(b^h \times a-k)\)

Part3. 代码

#include<iostream>
#include<cstdio>
using namespace std;
const int mod=1000000007;
long long pow(long long x,int y){//快速幂
	long long res=1;
	while(y){
		if(y&1){
			res=(res*x)%mod; 
		}
		x=(x*x)%mod;
		y=(y>>1);
	}
	return res;
}
int main() {
	int t;
	scanf("%d",&t);
	while(t--){
		int h;
		long long a,b;
		scanf("%lld%lld%d",&a,&b,&h);
		long long k=(pow(b,h)-1+mod)*pow(b-1,mod-2)%mod;
                                             //通过费马小定理求解逆元
		if(a>=b){
			if(b==1)printf("%lld\n",((a-1)*h+a)%mod);
			printf("%lld\n",(k*(a-b)%mod+pow(b,h)*a)%mod);
		}else if(a<b){
			printf("%lld\n",(k*(b-a)%mod+(pow(b,h)*a%mod-k*(b-a)%mod+mod))%mod);
		}
	}
	return 0;
}