网络流相关小结

之前网络流都是背板子和结论的，现在试图严谨地写一篇关于网络流的笔记。

网络流东西很多，一下子肯定总结不完，所以咕计是个咕咕项目。

@

目录

• 一、最大流
  • 简介和引入
  • Ford-Fulkerson 算法
  • Edmonds-Karp 算法
  • Dinic 算法
• 二、费用流
• 三、等价流树/最小割树

一、最大流

简介和引入

• 定义 1.1（网络）：网络是一张简单有向图 \(G=(V,E)\)，满足对于任意 \(u,v\in V\) 有 \((u,v),(v,u)\) 至多一者属于 \(E\)。有两个点 \(s,t\in V\)，它们分别被称作源点和汇点，满足 \(s\) 没有入边，\(t\) 没有出边。有容量函数 \(c:V\times V\to \mathbb R\)，满足 \(c(u,v)\) 非负，且对于任意 \((u,v)\not\in E\) 有 \(c(u,v)=0\)。

为了方便，我们接下来的讨论都在某个网络 \(G\) 上进行。记 \(n=|V|,m=|E|\)。

• 定义 1.2（流函数）：称函数 \(f:V\times V\to \mathbb R\) 为网络 \(G\) 的流函数，当且仅当它满足：

  • 对于任意 \(u,v\in V\)，有 \(f(u,v)\leq c(u,v)\)。
  • 对于任意 \(u,v\in V\)，有 \(f(v,u)=-f(u,v)\)。
  • 对于任意 \(u\in V\setminus\{s,t\}\)，有 \(\sum_{v}f(u,v)=0\)。

  定义流的大小为 \(|f|=\sum_{v}f(s,v)\)。称使得 \(|f|\) 最大的 \(f\) 为最大流。

依据这三条，经过代数推导可以证明出其他一些关于流函数的直观性质：

• 引理 1.3：下述若干性质成立。
  1. \(\sum_u\sum_vf(u,v)=0\)。
  2. \(\sum_{v}f(s,v)=\sum_vf(v,t)\)。
  3. 对于任意 \((u,v)\in E\)，有 \(0\leq f(u,v)\leq c(u,v)\)；对于任意 \((u,v)\not\in E\) 且 \((v,u)\not\in E\)，有 \(f(u,v)=0\)。

求最大流的主体思想是增广。我们先介绍增广的定义。

• 定义 1.4（残量网络）：定义残量函数 \(r(u,v)=c(u,v)-f(u,v)\)。

  定义残量网络为图 \(G_f=(V_f,E_f)\)，其中 \(V_f=V\)，\(E_f=\{(u,v):u\in V,v\in V,r(u,v)>0\}\)。

  有时我们将在 \(E_f\) 中的边称为非饱和边，将不在 \(E_f\) 中的边称为饱和边。

• 引理 1.5：下述若干性质成立。

  1. 对于任意 \(u,v\in V\)，\(r(u,v)\geq 0\)。
  2. 对于任意 \((u,v)\in E_f\)，必有 \((u,v)\in E\) 或 \((v,u)\in E\)。
  3. 对于任意 \(u\in V\setminus\{s,t\}\)，有 \(\sum_vr(u,v)=\sum_vc(u,v)\)。

• 定义 1.6（增广）：增广路是 \(G_f\) 中一条 \(s\) 到 \(t\) 的路径。

  定义某流 \(f\) 根据 \(G_f\) 上的增广路 \(P=(u_1=s,u_2,\cdots,u_{k-1},u_k=t)\) 增广为如下操作：记 \(r(P)=\min_{i=1}^{k-1}r(u_i,u_{i+1})\)，然后对于每个 \(i\in [1,k)\)，令 \(f(u_i,u_{i+1})\) 加上 \(r(P)\)、\(f(u_{i+1},u_i)\) 减去 \(r(P)\)（对应地会使 \(r(u_i,u_{i+1})\) 减去 \(r(P)\)、\(r(u_{i+1},u_i)\) 加上 \(r(P)\)）。容易验证此时 \(f\) 仍为一个合法的流，且 \(|f|\) 增加了 \(w\)。

我们的想法是不断地在残量网络上找增广路并进行增广，最后得到最大流。但在此之前，我们需先证明找不到增广路等价于找到了最大流，这是容易被忽略的。为此，我们引入割的概念。

• 定义 1.7（割）：称 \((S,T)\) 是网络 \(G\) 的割，当且仅当 \(S\cup T=V,S\cap T=\varnothing\) 且 \(s\in S,t\in T\)。

  定义割 \((S,T)\) 的流量为：\(f(S,T)=\sum_{u\in S}\sum_{v\in T}f(u,v)\)。

  定义割 \((S,T)\) 的容量为：\(c(S,T)=\sum_{u\in S}\sum_{v\in T}c(u,v)\)。

  称使得 \(c(S,T)\) 最小的 \((S,T)\) 为最小割。

• 引理 1.8：设 \(f\) 是 \(G\) 的一个流，\((S,T)\) 是 \(G\) 的一个割，那么 \(|f|=f(S,T)\)。

  证明：如下：

  \[f(S,T)=\sum_{u\in S}\sum_{v\in T}f(u,v)=\sum_{u\in S}\sum_{v\in T}f(u,v)+\sum_{u\in S}\sum_{v\in S}f(u,v)=\sum_{u\in S}\sum_{v}f(u,v)=\sum_v f(s,v)=|f| \]

• 推论 1.9：最大流小于等于最小割。

  证明：设 \(f\) 是 \(G\) 的一个流，\((S,T)\) 是 \(G\) 的一个割，那么 \(|f|=f(S,T)=\sum_{u\in S}\sum_{v\in T}f(u,v)\leq \sum_{u\in S}\sum_{v\in T}c(u,v)=c(S,T)\)。

• 定理 1.10（最大流最小割定理）：设 \(f\) 是 \(G\) 的一个流。那么如下三个命题是等价的：

  1. \(f\) 是 \(G\) 的最大流。
  2. \(G_f\) 不包含任何增广路。
  3. 存在某个 \(G\) 的割 \((S,T)\)，满足 \(|f|=c(S,T)\)。

  证明：\((1)\Rarr(2)\)：显然。

  \((2)\Rarr(3)\)：令 \(S=\{v\in V:G_f\text{中存在一条}s\text{到}v\text{的路径}\}\)，\(T=V\setminus S\)，显然 \(s\in S\) 且 \(t\in T\)。根据定义，对于任意 \(u\in S\) 且 \(v\in T\) 都有 \(r(u,v)=0\)，那么 \(\sum_{u\in S}\sum_{v\in T}r(u,v)=0\) 即 \(\sum_{u\in S}\sum_{v\in T}c(u,v)=\sum_{u\in S}\sum_{v\in T}f(u,v)\)，那么 \(c(S,T)=f(S,T)=|f|\)。

  \((3)\Rarr(1)\)：显然。

于是，根据定理 1.10，我们得到了一个求解最大流的算法：不断地在残量网络上找增广路并进行增广，直到找不到增广路为止。注意增广的次数是有限的，因为每次增广后最大流都会严格增大，而最大流是有限的。

定理 1.10 的证明实际上也给出了由最大流方案构造最小割方案的方法。

Ford-Fulkerson 算法

直接在残量网络上 dfs 找增广路。单次增广时间复杂度 \(O(m)\)。增广的次数：对于容量均为整数的情况，增广次数有上界 \(O(\text{最大流大小})\)；对于容量为有理数的情况，可以通过乘以某个系数使得它们转为整数；对于容量为无理数的情况，Ford-Fulkerson 算法可能会无限进行下去。

Edmonds-Karp 算法

考虑用 bfs 找增广路，单次增广时间复杂度仍然是 \(O(m)\) 的，但增广次数有了更好的上界 \(O(nm)\)，接下来我们来证明此事。

记 \(d(s,v)\) 为当前残量网络上 \(s\) 到 \(v\) 的最短路径长度（经过边数最少），若不存在则记为 \(\infty\)。于是 bfs 树就是最短路径树。

• 引理 1.11：EK 算法过程中，\(d(s,v)\) 单调不减。

  证明：考虑某次增广，我们在 \(G_f\) 上找到了增广路 \(P=(u_1=s,u_2,\cdots,u_{k-1,}u_k=t)\)，那么对于任意 \(i\in[1,k)\) 有 \(d(s,u_{i+1})=d(s,u_i)+1\)。我们可能会对 \(G_f\) 进行的改变有：删掉某条正向边 \((u_i,u_{i+1})\)、增加某条反向边 \((u_{i+1},u_i)\)。

  考虑先进行增加反向边的操作，我们只需证明增加了反向边 \((u_{i+1},u_i)\) 后，\(d(s,u_i)\) 不会变小即可：变小了则意味着 \(d(s,u_i)>d(s,u_{i+1})+1\)，这与 \(d(s,u_i)+1=d(s,u_{i+1})\) 矛盾。

  再考虑进行删掉正向边的操作，显然删除一条边不会让图中任何一个点的最短路变小。

• 定义 1.12（关键边）：对于残量网络 \(G_f\) 上的某条增广路 \(P=(u_1=s,u_2,\cdots,u_{k-1},u_k=t)\)，称 \((u_i,u_{i+1})\) 为 \(P\) 上的关键边，当且仅当 \(r(u,v)=r(P)\)。

• 引理 1.13：设残量网络 \(G_f\)，其上的某条增广路 \(P\)，和 \(P\) 上的任意关键边 \((u,v)\)。设 \(f'\) 为 \(f\) 根据 \(P\) 增广后的流，那么 \((u,v)\not \in G_{f'}\)。

• 定理 1.14：EK 算法过程的增广总次数为 \(O(nm)\)。

  证明：对于某条边 \((u,v)\)，设其在某一次成为关键边时对应的残量网络上的最短路函数为 \(d\)。设 \((u,v)\) 下一次成为关键边时，对应的最短路函数为 \(d''\)。而在 \((u,v)\) 两次成为关键边之间，\((v,u)\) 肯定要先成为一次关键边，设此时的最短路函数为 \(d'\)。那么：

  \[d''(s,u)\geq d'(s,u)=d'(s,v)+1\geq d(s,v)+1=(d(s,u)+1)+1=d(s,u)+2 \]

  于是，在某条边 \((u,v)\) 两次成为关键边之间，\(d(s,u)\) 必定至少增加 \(2\)，而一旦 \(d(s,u)\geq n\) 就不可能再变大，于是 \((u,v)\) 至多成为 \(\frac n2\) 次关键边。每次增广时，至少有一条边成为关键边，而可能成为关键边的边数至多为 \(2m\)，于是至多增广 \(2m\cdot \frac n2=nm\) 次。

于是我们得到了时间复杂度为 \(O(nm^2)\) 的 EK 算法，这是和容量无关的。

Dinic 算法

dinic 算法的主体思想仍然是增广，它的算法过程如下：每次先在残量网络上 bfs 建立最短路 DAG（它是个分层图），然后一直在这个 DAG 上找增广路，直到找不到为止才再次分层。

我们把 “分层成 DAG 后，在 DAG 上多次增广” 这个过程称为一轮。

分析一轮的时间复杂度：每次增广至少有一条关键边，而每条关键边的反向边不可能出现在 DAG 中，于是至多增广 \(m\) 次。那么粗糙分析的话，每次增广用 \(O(m)\) 的时间，整轮下来是 \(O(m^2)\) 的。但实际上，如果我们加上当前弧优化，每次找增广路就能做到 \(O(n)\)（注意增广路长度至多为 \(n\)），一轮的复杂度降为 \(O(nm)\)。

接下来我们证明至多会进行 \(O(n)\) 轮。

• 定理 1.15：dinic 算法过程中，每经过一轮，\(d(s,t)\) 严格变大。

  证明：考虑某一轮对应的 DAG 为 \(D\)。该轮进行完后，会删掉一些 \(D\) 上的正向边，增加一些 \(D\) 上正向边对应的反向边。那么下一轮时，残量网络上剩下的边只有两种可能：\(D\) 上的边，\(D\) 上从远层往近层连的边（一部分是本来就不在 \(D\) 中的，一部分是刚刚一轮新增的反向边）。而且不存在只包含第一种边的 \(s\) 到 \(t\) 的路径。于是在这张图上，\(s\) 到 \(t\) 的最短路一定严格变大了。

又由于一旦 \(d(s,t)\geq n\) 就不可能再变大，于是至多会进行 \(n\) 轮分层。于是 dinic 算法的时间复杂度为 \(O(n^2m)\)。

一个优化是 bfs 分层时遇到 \(t\) 就停止，这在随机数据下能起到不错的效果。

Dinic 算法求解二分图最大匹配问题

• 定义 1.16（单位网络）：称网络 \(G\) 是单位网络，当且仅当对于任意 \(u,v\in V\) 有 \(c(u,v)\in\{0,1\}\)。

• 引理 1.17：对单位网络 \(G\) 进行一次增广后，得到的残量网络仍为单位网络。

• 引理 1.18：对单位网络 \(G\) 运行 dinic 算法，每轮增广的时间复杂度均为 \(O(m)\)。

• 定理 1.19：对单位网络 \(G\) 运行 dinic 算法，至多会进行 \(O(\min(m^{1/2},n^{2/3}))\) 轮增广。

  证明：至多会进行 \(O(m^{1/2})\) 轮增广：

  假设已经进行了 \(m^{1/2}\) 轮增广，并得到残量网络 \(G_f\)，我们现在要在 \(G_f\) 上找最大流。设 \(G_f\) 最大流大小为 \(p\)，这在 \(G_f\) 上对应 \(p\) 条 \(s\) 到 \(t\) 的路径。\(G_f\) 上至多有 \(2m\) 条边，而根据定理 1.15 可知此时 \(d(s,t)\geq m^{1/2}\)，于是 \(p\leq 2m^{1/2}\)，于是在 \(G_f\) 上至多增广 \(O(m^{1/2})\) 轮。

  至多会进行 \(O(n^{2/3})\) 轮增广：

  假设已经进行了 \(2n^{2/3}\) 轮增广，并得到残量网络 \(G_f\)，我们现在要在 \(G_f\) 上找最大流。将 \(G_f\) 按最短路长度分层，至少有 \(2n^{2/3}\) 层，那么一定存在相邻两层使得这两层的点数都小于等于 \(n^{1/3}\)，否则点数大于 \(n^{1/3}\) 的层数一定过半，那么总点数就大于 \(n\) 了。考虑以这相邻两层之间为界划分为 \(S,T\) 集，得到 \(G\) 的一个割，且割的大小不超过 \((n^{1/3})^2=n^{2/3}\)，而最大流小于等于最小割，所以在 \(G_f\) 上至多增广 \(O(n^{2/3})\) 轮。

• 定理 1.20：设 \(G\) 是单位网络，且除了 \(s,t\) 外的每个点 \(u\)，都满足 \(u\) 的入边或出边只有一条。那么对 \(G\) 运行 dinic 算法，至多会进行 \(O(n^{1/2})\) 轮增广。

  证明：与引理 1.19 中 “至多会进行 \(O(m^{1/2})\) 轮增广” 的证明类似。需要注意的是，根据引理 1.5.3，\(G_f\) 上仍满足除了 \(s,t\) 外的每个点 \(u\)，\(u\) 的入边或出边只有一条。

根据定理 1.20，可知 dinic 求解二分图最大匹配的时间复杂度是 \(O(m\sqrt n)\) 的。

二、费用流

咕。

三、等价流树/最小割树

设无向图 \(G=(V,E)\) 和函数 \(c:E\to[0,+\infty)\)。

设 \(u,v\) 间所有最小割构成的集合为 \(\alpha(u,v)\)，即 \(W\in \alpha(u,v)\) 等价于 \((W,V-W)\) 是 \((u,v)\) 的一组最小割。设 \((u,v)\) 的最小割的权值是 \(\lambda(u,v)\)。

• 引理 1：设 \(a,b,c\in V\) 且它们两两不同，那么 \(\lambda(a,b)\geq \min(\lambda(a,c),\lambda(b,c))\)。

  证明：任选 \(A\in\alpha(a,b)\) 且 \(a\in A\)。不妨设 \(c\in A\)，那么 \((A,B)\) 也是 \((c,b)\) 的一组割，从而 \(\lambda(b,c)\leq \lambda(a,c)\)。

• 推论 2：设 \(a,b,c\in V\)，那么 \(\lambda(a,b),\lambda(a,c),\lambda(b,c)\) 中至少有两个相同的最小值。

• 推论 3：设 \(u,v,w_1,\cdots,w_k\in V\) 且它们两两不同，那么 \(\lambda(u,v)\geq \min(\lambda(u,w_1),\lambda(w_1,w_2),\cdots,\lambda(w_k,v))\)。

设 \(f(U)\) 为 \(\sum_{(u,v)\in E,u\in U,v\in V\setminus U} c(e)\)。

• 引理 4：对于任意 \(A,B\subseteq V\)，\(f(A)+f(B)\geq f(A\cup B)+f(A\cap B)\)。

  证明：如图：

  

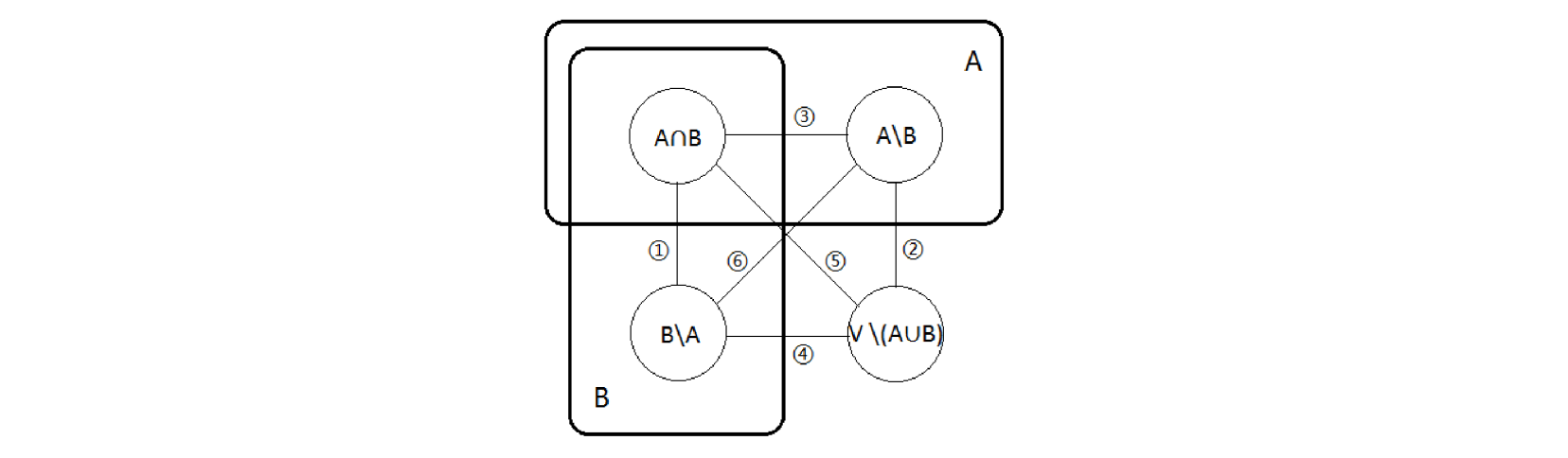
  那么：

  \[\begin{aligned} f(A)+f(B)&=①+②+③+④+2⑤+2⑥\\ f(A\cup B)+f(A\cap B)&=①+②+③+④+2⑤ \end{aligned} \]

• 引理 5：对于任意 \(A,B\subseteq V\)，\(f(A)+f(B)\geq f(A\setminus B)+f(B\setminus A)\)。

  证明：

  \[\begin{aligned} f(A)+f(B)&=f(V\setminus A)+f(B)\\ &\geq f((V\setminus A)\cup B)+f((V\setminus A)\cap B)\\ &=f(A\setminus B)+f(B\setminus A) \end{aligned} \]

• 引理 6：设 \(s,t\in V\) 且 \(s\neq t\)，\(W\in \alpha(s,t)\) 且 \(s\in W\)，\(u,v\in W\) 且 \(u\neq v\)。

  那么对于任意 \(X\in\alpha(u,v)\)，有 \(X\cap W\in\alpha(u,v)\) 或 \(W\setminus X\in\alpha(u,v)\)。即存在一组最小割 \(X'\in\alpha(u,v)\)，使得 \(X'\subseteq W\) 且 \(X'\) 和 \(X\) 在 \(W\) 中的划分相同。

  证明：不妨设 \(s,u\in X\)。

  	\(\in W\)	\(\in X\)
  \(s\)	1	1
  \(t\)	0	?
  \(u\)	1	1
  \(v\)	1	0

  • 若 \(t\not \in X\)。根据引理 4 有 \(f(X)+f(W)\geq f(X\cap W)+f(X\cup W)\)。

    显然 \(X\cap W\) 也是 \((u,v)\) 的一组割那么 \(f(X\cap W)\leq f(X)\)；\(X\cup W\) 也是 \((s,t)\) 的一组割那么 \(f(X\cup W)\leq f(W)\)。

    于是 \(f(X)=f(X\cap W)\) 且 \(f(W)=f(X\cup W)\)，那么可以把 \(X\) 调整为 \(X\cap W\)，它仍为 \((u,v)\) 的一组最小割。

  • 若 \(t\in X\)。根据引理 5 有 \(f(X)+f(W)\geq f(W\setminus X)+f(X\setminus W)\)。

    显然 \(W\setminus X\) 也是 \((u,v)\) 的一组割，\(X\setminus W\) 也是 \((s,t)\) 的一组割。

    于是可以把 \(X\) 调整为 \(W\setminus X\)，它仍为 \((u,v)\) 的一组最小割。

考虑一棵点集仍为 \(V\) 的新图 \(T\) 和如下过程 solve(W)，其中 \(W\subseteq V\)：

若 \(|W|=1\) 则返回。否则任意选择 \(s,t\in W\) 且 \(s\neq t\)，求出 \(s,t\) 的任意一组最小割 \(X\in\alpha(s,t)\)，然后在 \(T\) 中 \(s,t\) 间连上一条权值为 \(\lambda(s,t)\) 的边，然后递归子过程 solve(W cap X) 和 solve(W setminus X)。

令 \(T\) 初始无边，那么进行 solve(V) 后 \(T\) 将会变成一棵树。

• 引理 7：对于任意 \(u,v\in V\) 且 \(u\neq v\)，\(\lambda(u,v)\) 就是 \(T\) 中 \(u,v\) 路径上边权最小值。

  证明：设 \(u,v\) 在 solve(V) 的某子过程 solve(W) 中分离，即 \(u\in W\cap X\) 且 \(v\in W\setminus X\)。设 \(u,v\) 在树上的路径为 \(w_1=u,\cdots,w_k=v\)，其中 \(w_p=s\) 且 \(w_{p+1}=t\)。该路径上的边权分别为 \(\lambda(w_1,w_2),\cdots,\lambda(w_{k-1},w_k)\)。

  根据推论 3，可知 \(\lambda(u,v)\geq \min(\lambda(w_1,w_2),\cdots,\lambda(w_{k-1},w_k))\)，现在欲证明左式小于等于右式。

  归纳地假设结论对于 solve(W) 的子过程都是成立的，那么只需证明 \(\lambda(u,v)\leq \min(\lambda(u,s),\lambda(s,t),\lambda(t,v))\)。首先 \(u\in X\) 且 \(v\not\in X\) 有 \(\lambda(u,v)\leq \lambda(s,t)\)。

  根据引理 6，存在 \(Y\subseteq X\) 使得 \(Y\in\alpha(u,s)\)。

  • 若 \(u\in Y\)。由于 \(W\setminus X\subseteq V\setminus X\subseteq V\setminus Y\)，那么 \(Y\) 也是 \(u,v\) 的一组割，从而 \(\lambda (u,v)\leq \lambda(u,s)\)。
  • 若 \(s\in Y\)。同理 \(Y\) 也是 \(s,t\) 的一组割，从而 \(\lambda(s,t)\leq \lambda(u,s)\)，那么 \(\lambda(u,v)\leq \lambda(s,t)\leq \lambda(u,s)\)。

\(T\) 就是所谓的等价流树。

最小割树和等价流树类似，但能保证删去树上一条边后得到的两个连通块就是该边端点间的一组最小割。构造要麻烦一些，先略。