深度学习笔记_Week1
本笔记基于吴恩达深度学习deeplearning.ai课程
第二周:神经网络的编程基础
神经网络的训练过程可以分为前向传播和反向传播两个独立的部分
2.1 二分类(Binary Classification)
所谓二分类问题,可以参照以下例子
假如你有一张图片作为输入,比如这只猫,如果识别这张图 片为猫,则输出标签 1 作为结果;如果识别出不是猫,那么输出标签 0 作为结果。
在二分类问题中,目标就是习得一个分类器,它以图片的特征向量作为输入,然后预测输出结果 𝑦 为 1 还是 0
𝑋 = [𝑥 (1) , 𝑥 (2) , . . . , 𝑥 (𝑚) ]:表示所有的训练数据集的输入值,放在一个 𝑛𝑥 × 𝑚的矩阵中, 其中𝑚表示样本数目
𝑌 = [𝑦 (1) , 𝑦 (2) , . . . , 𝑦 (𝑚) ]:对应表示所有训练数据集的输出值,维度为1 × 𝑚。
用一对(𝑥, 𝑦)来表示一个单独的样本,𝑥代表𝑛𝑥维的特征向量,𝑦 表示标签(输出结果)只能为 0 或 1。 而训练集将由𝑚个训练样本组成,其中(𝑥 (1) , 𝑦 (1) )表示第一个样本的输入和输 出,(𝑥 (2) , 𝑦 (2) )表示第二个样本的输入和输出,直到最后一个样本(𝑥 (𝑚) , 𝑦 (𝑚) ),然后所有的这些一起表示整个训练集。
总的来说,𝑋是一个规模为𝑛𝑥乘以𝑚的矩阵,𝑌是一个规模为 1 乘以𝑚的矩阵。
2.2 逻辑回归(Logistic Regression)
逻辑回归通过计算 y^ 来实现对实际值 y 的估计,一件可以尝试却不可行的事是让𝑦^ = 𝑤𝑇𝑥 + 𝑏 ,因为我们希望的 y^ 值域为0到1,故要使用sigmoid函数。
sigmoid函数很好地将所有的z值映射到 0 到 1 之间。
2.3 逻辑回归的代价函数(Logistic Regression Cost Function)
为什么需要代价函数:
为了训练逻辑回归模型的参数参数𝑤和参数𝑏我们,需要一个代价函数,通过训练代价函数来得到参数𝑤和参数𝑏。
损失函数:
损失函数又叫做误差函数,用来衡量算法的运行情况,Loss function:𝐿(𝑦^ , 𝑦). 我们通过这个𝐿称为的损失函数,来衡量预测输出值和实际值有多接近。一般我们用预测值和实际值的平方差或者它们平方差的一半,但是通常在逻辑回归中我们不这么做,因为梯度下降法很可能找不到全局最优值,在逻辑回归模型中会定义另外一个损失函数。 我们在逻辑回归中用到的损失函数是:𝐿(𝑦^ , 𝑦) = −𝑦log(𝑦^) − (1 − 𝑦)log(1 − 𝑦^)
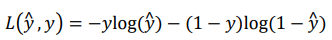
代价函数:
算法的代价函数是对𝑚个样本的损失函数求和然后除以m:
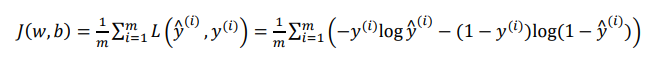
损失函数只适用于单个训练样本,而代价函数是参数的总代价,所以在训练逻辑回归模型时候,我们需要找到合适的𝑤和𝑏,来让代价函数 𝐽 的总代价降到最低。
2.4 梯度下降法(Gradient Descent)
即以求导数的方法不断地逼近全局最优解,即代价函数 𝐽 这个凸函数的最小值点
对于w和b,使用所有样本不断进行以下迭代:
其中 α 为学习率,用于控制步长(一次迭代移动的距离)
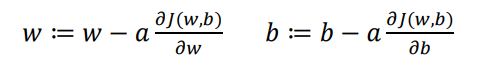
2.5 导数(Derivatives)
2.6 更多的导数例子(More Derivative Examples)
略
2.7 计算图(Computation Graph)
一个神经网络的计算,都是按照前向或反向传播过程组织的。首先我们计算出一个新的网络的输出(前向过程),紧接着进行一个反向传输操作。后者我们用来计算出对应的梯度或导数。
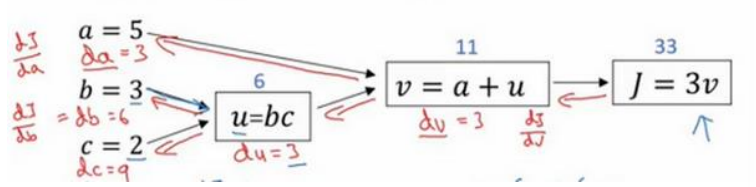
以下为课上计算图的例子:
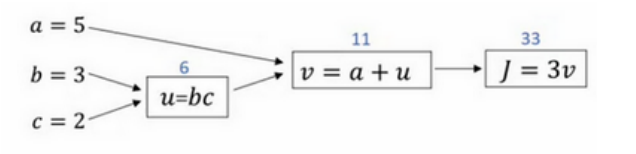
所谓前向传播即从左到右进行计算,由abc到 𝐽 的过程,而得到 𝐽 后从右向左计算得到 𝐽 对各个变量的偏导数的过程即为反向传播。
2.8 使用计算图求导数(Derivatives with a Computation Graph)
计算的最终目标是 𝐽 对 a、b、c 的偏导数(因为我们的目的是通过偏导数进行梯度下降),可以通过高数的链式求导法则进行轻松计算,由于中间过程量以及最终结果在前向传播中已经计算得出,因此可以反向通过微分的方式逐一求出偏导数,直至最左边,此即反向传播。
2.9 逻辑回归中的梯度下降(Logistic Regression Gradient Descent)
简单推导一下w和b的偏导数

对于每个样本,要做的几件事是:
- 计算dz
- 根据dz计算dw、db
- 梯度下降,得到新的w和b的值



