随机变量、分布函数
随机变量
定义：对样本空间，有一个实值函数X=X(w)，使每个实验结果关联一个特定的数，这种实验结果与数的对应关系形成随机变量。我们将实验结果所对应的数称为随机变量的取值。（简单的说每个实验结果用一个数来表示，这样在数学上比较方便）
对随机变量进行分类有：离散型随机变量、非离散型随机变量。
所谓离散型随机变量就是这个实值函数的取值范围是有限多个，或者无限可列个（如0，1，-1，2，-2……）；而非离散型随机变量则主要关注连续型，取值为一个或多个区间。
离散型随机变量及其概率分布
对X的所有可列个取值 xk (k=1,2,3...)
称为X的概率函数（分布律、分布列）
将其表格形式称为概率分布表
如：
| X | 0 | 1 |
|---|---|---|
| P | 1/2 | 1/2 |
画成图像称为概率分布图
图中所有线段的长度相加为1（全集)
连续型随机变量及其概率密度函数
和离散型类似，但是此时是在连续区间上进行讨论
通常用频率分布直方图来表示：
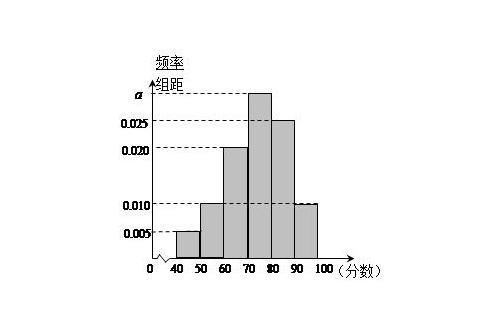
注意纵坐标为频率/组距
1）每个矩形的面积为该组的频率
2）所有矩形的面积和为1
3）介于x=a,x=b之间矩形的面积近似于(a,b]的频率
随着组距越来越小，图像越来越像光滑曲线，设曲线解析式为y=f(x)，则将f称为概率分布密度函数
严谨定义：若非负可积函数f(x)，且f(x)>=0（因为频率肯定大于等于0），对任何a<=b，P{a<x<=b}等于f(x)从a到b的积分，则称f(x)为x的概率分布密度函数
1）f(x)>=0
2）f(x)从负无穷大到正无穷大积分和为1
3）连续变量取个别值的概率为0
由3）可知，连续型随机变量区间端点有没有无所谓
由此观之：
概率为0的事件未必是不可能事件
概率为1的事件未必是必然事件
因为f(x)可积，所有用积分的方式求区间的概率，注意f(x)和所求区间之间的关系，避免求错
例如：求
从1.5到2.5的积分，要注意到2到2.5的概率为0，不要用-0.5x+1带入。
前文提到过，连续变量取个别值的概率为0，那么概率函数的值的意义究竟是什么呢？
f(x)的值为X取x附近值的概率大小
分布函数
在离散型随机变量的连续区间上，定义F(x)，使得
即X取值不超过x的概率
则称F(x)为X的分布函数
性质：
1）0<=F(x)<=1，-∞<x<+∞
2）F(x)是一个不减函数，即若x1<x2则F(x1)<=F(x2)
F(+∞)=1,F(-∞)=0,这个性质用于求参数
例如：
\[F(x)=a-e^{-x} \]F(+∞)=a=1，得a=1
3）F(x)右连续
离散型为右连续，连续型不仅右连续而且连续
注：右连续是指函数在一点右侧连续，若一元函数f在x0处的右极限为f(x0)，即f(x0+0)=f(x0)，则称f在x0处右连续。函数f在x0处右连续是函数f在x0处连续的必要不充分条件。当函数f在x0处既左连续又右连续时，函数f在x0处连续。
由此观之，有：
1）P{x<=a}=F(a)
2）P{x>a}=1-P{x<=a}=1-F(a)
3）P{a<x<=b}=P{x<=b}-P{x<=a}=F(b)-F(a)
4）P{x=a}=F(a)-F(a-0) (注：F(a)相当于x≤a，也就是-∞到a的长度，而点的长度是0，F（a-0）相当于把a的长度减去，即x<a)
5）P{a<=x<=b}=F(b)-F(a-0)
6）P{x<a}=F(a-0)
7）P{x>=a}=1-P{x<a}=1-F(a-0)
前文提到连续变量的取个别值的概率为0，取不取端点无所谓，以上七个公式针对的是离散型随机变量
离散型随机变量的分布函数
《概率论与数理统计》教学视频全集（宋浩）：16m~32m
这是一个概率逐步累积的过程
已知分布函数求概率函数
间断点xk（即区间端点）是X的取值
P{X=xk}=F(xk)-F(xk-0)
连续型随机变量的分布函数
对于连续型随机变量，F(x)等于从负无穷到x对随机变量函数f(x)求积分
即F'(x)=f(x)
前文提到连续变量的取个别值的概率为0，取不取端点无所谓，给计算带来很大便利
