Educational Codeforces Round 171 div2(A~E)
Educational Codeforces Round 171 div2(A~E)
Dashboard - Educational Codeforces Round 171 (Rated for Div. 2) - Codeforces
火车头
#define _CRT_SECURE_NO_WARNINGS 1
#include <algorithm>
#include <array>
#include <bitset>
#include <cassert>
#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <chrono>
#include <fstream>
#include <functional>
#include <iomanip>
#include <iostream>
#include <iterator>
#include <list>
#include <map>
#include <numeric>
#include <queue>
#include <random>
#include <set>
#include <stack>
#include <string>
#include <tuple>
#include <unordered_map>
#include <utility>
#include <vector>
using namespace std;
#define ft first
#define sd second
#define yes cout << "yes\n"
#define no cout << "no\n"
#define Yes cout << "Yes\n"
#define No cout << "No\n"
#define YES cout << "YES\n"
#define NO cout << "NO\n"
#define pb push_back
#define eb emplace_back
#define all(x) x.begin(), x.end()
#define all1(x) x.begin() + 1, x.end()
#define unq_all(x) x.erase(unique(all(x)), x.end())
#define unq_all1(x) x.erase(unique(all1(x)), x.end())
#define sort_all(x) sort(all(x))
#define sort1_all(x) sort(all1(x))
#define inf 0x3f3f3f3f
#define infll 0x3f3f3f3f3f3f3f3fLL
#define RED cout << "\033[91m" // 红色
#define GREEN cout << "\033[92m" // 绿色
#define YELLOW cout << "\033[93m" // 蓝色
#define BLUE cout << "\033[94m" // 品红
#define MAGENTA cout << "\033[95m" // 青色
#define CYAN cout << "\033[96m" // 青色
#define RESET cout << "\033[0m" // 重置
template <typename T>
void Debug(T x, int color = 1)
{
switch (color)
{
case 1:
RED;
break;
case 2:
YELLOW;
break;
case 3:
BLUE;
break;
case 4:
MAGENTA;
break;
case 5:
CYAN;
break;
default:
break;
}
cout << x;
RESET;
}
typedef long long ll;
typedef unsigned long long ull;
typedef long double ld;
// typedef __int128_t i128;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
typedef pair<ld, ld> pdd;
typedef pair<ll, int> pli;
typedef pair<string, string> pss;
typedef pair<string, int> psi;
typedef pair<string, ll> psl;
typedef tuple<int, int, int> ti3;
typedef tuple<ll, ll, ll> tl3;
typedef tuple<ld, ld, ld> tld3;
typedef vector<bool> vb;
typedef vector<int> vi;
typedef vector<ll> vl;
typedef vector<string> vs;
typedef vector<pii> vpii;
typedef vector<pll> vpll;
typedef vector<pli> vpli;
typedef vector<pss> vpss;
typedef vector<ti3> vti3;
typedef vector<tl3> vtl3;
typedef vector<tld3> vtld3;
typedef vector<vi> vvi;
typedef vector<vl> vvl;
typedef queue<int> qi;
typedef queue<ll> ql;
typedef queue<pii> qpii;
typedef queue<pll> qpll;
typedef queue<psi> qpsi;
typedef queue<psl> qpsl;
typedef priority_queue<int> pqi;
typedef priority_queue<ll> pql;
typedef map<int, int> mii;
typedef map<int, bool> mib;
typedef map<ll, ll> mll;
typedef map<ll, bool> mlb;
typedef map<char, int> mci;
typedef map<char, ll> mcl;
typedef map<char, bool> mcb;
typedef map<string, int> msi;
typedef map<string, ll> msl;
typedef map<int, bool> mib;
typedef unordered_map<int, int> umii;
typedef unordered_map<ll, ll> uml;
typedef unordered_map<char, int> umci;
typedef unordered_map<char, ll> umcl;
typedef unordered_map<string, int> umsi;
typedef unordered_map<string, ll> umsl;
std::mt19937_64 rng(std::chrono::steady_clock::now().time_since_epoch().count());
template <typename T>
inline T read()
{
T x = 0;
int y = 1;
char ch = getchar();
while (ch > '9' || ch < '0')
{
if (ch == '-')
y = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9')
{
x = (x << 3) + (x << 1) + (ch ^ 48);
ch = getchar();
}
return x * y;
}
template <typename T>
inline void write(T x)
{
if (x < 0)
{
putchar('-');
x = -x;
}
if (x >= 10)
{
write(x / 10);
}
putchar(x % 10 + '0');
}
/*#####################################BEGIN#####################################*/
void solve()
{
}
int main()
{
ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0);
// freopen("test.in", "r", stdin);
// freopen("test.out", "w", stdout);
int _ = 1;
std::cin >> _;
while (_--)
{
solve();
}
return 0;
}
/*######################################END######################################*/
// 链接：
A. Perpendicular Segments
给定一个坐标平面和三个整数 \(X\)、\(Y\) 和 \(K\)。找出两条线段 \(AB\) 和 \(CD\)，使得
- 点 \(A\)、\(B\)、\(C\) 和 \(D\) 的坐标为整数；
- \(0 \leq A_x, B_x, C_x, D_x \leq X\) 和 \(0 \leq A_y, B_y, C_y, D_y \leq Y\)；
- 线段 \(AB\) 的长度至少为 \(K\)；
- 线段 \(CD\) 的长度至少为 \(K\)；
- 线段 \(AB\) 和 \(CD\) 垂直：如果绘制包含 \(AB\) 和 \(CD\) 的线，它们将以直角相交。
请注意，线段不必须相交。只要它们导出的线垂直，线段就是垂直的。
输入
第一行包含一个整数 \(t\) ( \(1 \leq t \leq 5000\) ) — 测试用例的数量。接下来是 \(t\) 个用例。
每个测试用例的第一行也是唯一一行包含三个整数 \(X\)、\(Y\) 和 \(K\) ( \(1 \leq X, Y \leq 1000\) ; \(1 \leq K \leq 1414\) )。
对输入的附加约束：选择 \(X\)、\(Y\) 和 \(K\) 的值，使得答案存在。
输出
对于每个测试用例，打印两行。第一行应包含 \(4\) 个整数 \(A_x\)、\(A_y\)、\(B_x\) 和 \(B_y\) ——第一段的坐标。
第二行还应包含 \(4\) 个整数 \(C_x\)、\(C_y\)、\(D_x\) 和 \(D_y\) ——第二段的坐标。
如果有多个答案，请打印其中任何一个。
示例
输入
4
1 1 1
3 4 1
4 3 3
3 4 4
输出
0 0 1 0
0 0 0 1
2 4 2 2
0 1 1 1
0 0 1 3
1 2 4 1
0 1 3 4
0 3 3 0
提示
第一个测试用例的答案如下：
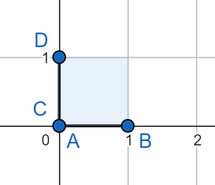
第二个测试用例的答案：
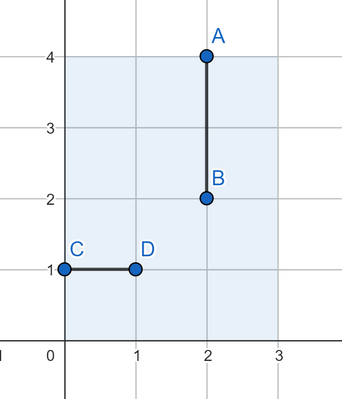
第三个测试用例的答案：
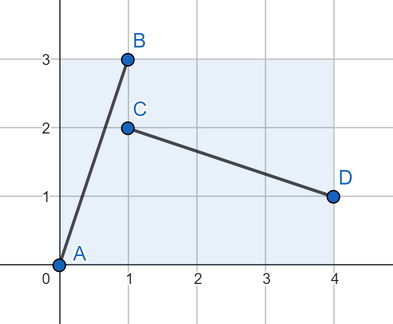
第四个测试用例的答案：
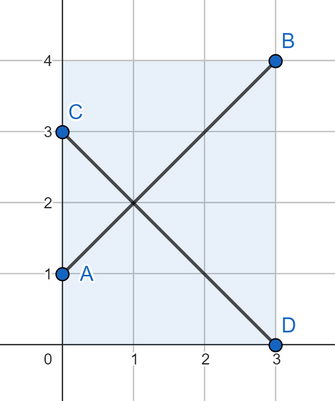
解题思路
对于矩形来说\(\max\{\min(|AB|,|CD|)\}=最大正方形对角线,AB \perp CD\)。
具体证明我也不太清楚该怎么证。
代码实现
void solve()
{
ll X, Y, K;
cin >> X >> Y >> K;
ll mn = min(X, Y);
cout << 0 << " " << 0 << " " << mn << " " << mn << "\n";
cout << 0 << " " << mn << " " << mn << " " << 0 << endl;
}
B. Black Cells
您将得到一个分成多个单元格的条带，从左到右编号为 \(0\) 至 \(10^{18}\)。最初，所有单元格都是白色的。
您可以执行以下操作：选择两个白色单元格 \(i\) 和 \(j\)，使得 \(i \neq j\) 和 \(|i - j| \leq k\)，并将它们涂成黑色。
给出了一个列表 \(a\)。此列表中的所有单元格都必须涂成黑色。此外，最多一个不在此列表中的单元格也可以涂成黑色。您的任务是确定 \(k\) 的最小值，以实现此目的。
输入
第一行包含一个整数 \(t\) (\(1 \leq t \leq 500\)) — 测试用例的数量。
每个测试用例的第一行包含一个整数 \(n\) (\(1 \leq n \leq 2000\))。
第二行包含 \(n\) 个整数 \(a_1, a_2, \ldots, a_n\) (\(0 < a_i < 10^{18}\); \(a_i < a_{i+1}\))。
对输入的附加约束：所有测试用例的 \(n\) 之和不超过 \(2000\)。
输出
对于每个测试用例，打印一个整数—— \(k\) 的最小值，可以将所有给定单元格涂成黑色。
示例
输入
4
2
1 2
1
7
3
2 4 9
5
1 5 8 10 13
输出
1
1
2
3
提示
在第一个示例中，\(k=1\) 时，可以涂黑单元格 \((1, 2)\)。
在第二个示例中，\(k=1\) 时，可以涂黑单元格 \((7, 8)\)。
在第三个示例中，\(k=2\) 时，可以涂黑单元格 \((2, 4)\) 和 \((8, 9)\)。
在第四个示例中，\(k=3\) 时，可以涂黑单元格 \((0, 1)\)、\((5, 8)\) 和 \((10, 13)\)。
解题思路
-
方法一
对于\(n\)为偶数的情况，一定是连续两个两个进行分配最优，对于奇数情况，我们可以枚举和列表外一起涂的单元格，剩下的单元格两个两个进行分配，统计最小值。
时间复杂度\(O(n^2)\)
-
方法二
题目要求最小化可行值，具有二分性，考虑二分\(k\)值。
对于一个指定的\(k\)值，我们可以使用使用\(dp\)去检验其是否可行。
设\(dp[i][j]\)为对于前\(i\)个元素，使用\(j\)次列表外元素是否可行，易得状态转移方程
\[dp[i][j]= \begin{cases} dp[i-2][j] & a[i]-a[i-1]\le k \\ dp[i-1][j-1] & a[i]-a[i-1]\gt k \end{cases} \]
时间复杂度\(O(n\log{V})\)
代码实现
方法一
void solve()
{
ll n;
cin >> n;
vl a(n);
for (int i = 0; i < n; i++)
{
cin >> a[i];
}
ll ans;
if (n % 2 == 0)
{
ans = 0;
for (int i = 1; i < n; i += 2)
{
ans = max(ans, a[i] - a[i - 1]);
}
}
else
{
ans = infll;
for (int i = 0; i < n; i++)
{
int cnt = 0;
int p = -1;
ll minK = 1;
for (int j = 0; j < n; j++)
{
if (j == i)
continue;
cnt++;
if (cnt == 1)
{
p = j;
}
else if (cnt == 2)
{
cnt = 0;
minK = max(minK, a[j] - a[p]);
}
}
ans = min(ans, minK);
}
}
cout << ans << '\n';
}
方法二
void solve()
{
int n;
cin >> n;
vl a(n + 1);
for (int i = 1; i <= n; i++)
{
cin >> a[i];
}
auto check = [&](ll k) -> bool
{
vector<vb> dp(n + 2, vb(2));
dp[0][0] = true; // 可以涂黑0个单元格
dp[1][1] = true; // 可以使用一次列表外单元格涂黑第一个单元格
for (int i = 2; i <= n + 1; i++)
{
for (int j = 0; j < 2; ++j)
{
if (!dp[i - 2][j]) // 如果当前状态不可达，跳过
continue;
// 尝试涂黑下一个单元格
if (a[i] - a[i - 1] <= k)
dp[i][j] = true; // 涂黑 a[i] 和 a[i-1]
// 如果还没有使用额外的单元格，尝试使用它
if (j == 0)
dp[i - 1][1] = true; // 涂黑 a[i-1] 和额外的单元格
}
}
return dp[n][0] || dp[n][1];
};
ll l = 1, r = 1e18;
while (l < r)
{
ll mid = (l + r) >> 1;
if (check(mid))
r = mid;
else
l = mid + 1;
}
cout << l << '\n';
}
C. Action Figures
Monocarp 家附近有一家商店出售可动人偶。一套新的可动人偶将很快发布；这套包含 \(n\) 个人偶，第 \(i\) 个人偶花费 \(i\) 枚硬币，可从第 \(i\) 天到第 \(n\) 天购买。
对于每 \(n\) 天，Monocarp 都知道他是否可以访问商店。
每次 Monocarp 访问商店时，他都可以购买商店中出售的任意数量的可动人偶（当然，他不能购买尚未可供购买的可动人偶）。如果 Monocarp 在同一天购买至少两个人偶，他将获得相当于他购买的最贵人偶价格的折扣（换句话说，他可以免费获得他购买的人偶中最贵的那个）。
Monocarp 想要从该套装中购买恰好一个第 \(1\) 个玩偶、一个第 \(2\) 个玩偶、...、一个第 \(n\) 个玩偶。他不能购买同一个玩偶两次。他必须花费的最低金额是多少？
输入
第一行包含一个整数 \(t\) (\(1 \leq t \leq 10^4\)) — 测试用例的数量。
每个测试用例由两行组成：
第一行包含一个整数 \(n\) (\(1 \leq n \leq 4 \cdot 10^5\)) — 集合中的数字数量（和天数）；
第二行包含一个字符串 \(s\) (\(|s|=n\)，每个 \(s_i\) 为 \(0\) 或 \(1\)）。如果 Monocarp 可以在第 \(i\) 天访问商店，则 \(s_i\) 为 \(1\)；否则，\(s_i\) 为 \(0\)。
对输入的其他约束：
在每个测试用例中，\(s_n\) 为 \(1\)，因此 Monocarp 总是能够在第 \(n\) 天购买所有数字；
所有测试用例的 \(n\) 之和不超过 \(4 \cdot 10^5\)。
输出
对于每个测试用例，打印一个整数 — Monocarp 必须花费的最低金额。
示例
输入
4
1
1
6
101101
7
1110001
5
11111
输出
1
8
18
6
提示
在第一个测试用例中，Monocarp 在第 \(1\) 天购买第 \(1\) 个人偶，花费 \(1\) 枚硬币。
在第二个测试用例中，Monocarp 可以在第 \(3\) 天购买第 \(1\) 和第 \(3\) 个人偶，在第 \(4\) 天购买第 \(2\) 和第 \(4\) 个人偶，在第 \(6\) 天购买第 \(5\) 和第 \(6\) 个人偶。然后，他将花费 \(1 + 2 + 5 = 8\) 枚硬币。
在第三个测试用例中，Monocarp 可以在第 \(3\) 天购买第 \(2\) 和第 \(3\) 个人偶，在第 \(7\) 天购买所有其他人偶。然后，他将花费 \(1 + 2 + 4 + 5 + 6 = 18\) 枚硬币。
解题思路
我们可以从后往前遍历每一天，记录可以购买的人偶。对于每一天，如果 Monocarp 可以访问商店并且有可购买的人偶，我们将其加入队列。
若当天无法购买人偶，我们可以把这个人偶和队列中的人偶进行匹配，将最贵的人偶零元购。
代码实现
void solve()
{
int n;
cin >> n;
string s;
cin >> s;
s = '#' + s;
ll sum = n * (1 + n) / 2; // 计算所有人偶的总花费
priority_queue<int> waitFree; // 大根堆存储等待零元购的人偶
for (int i = n; i >= 1; i--)
{
if (s[i] == '1')
{
waitFree.push(i); // 如果今天可以访问商店，加入待免费队列
}
else if (!waitFree.empty())
{
sum -= waitFree.top(); // 如果今天无法访问商店，取出最贵的人偶与当前人偶i进行匹配
waitFree.pop();
}
}
if (!waitFree.empty())
{
vi remain;
while (!waitFree.empty())
{
remain.eb(waitFree.top());
waitFree.pop();
}
for (int i = 0; i <= (int)remain.size() / 2 - 1; i++)
{
sum -= remain[i]; // 把最贵的那一半人偶零元购
}
}
cout << sum << endl;
}
D. Sums of Segments
给定一个整数序列 \([a_1, a_2, \ldots, a_n]\)。令 \(s(l, r)\) 为从 \(a_l\) 到 \(a_r\)（即 \(s(l, r) = \sum_{i=l}^r a_i\)）元素的总和。
让我们构建另一个大小为 \(\frac{n(n+1)}{2}\) 的序列 \(b\)，如下所示：
\(b = [s(1, 1), s(1, 2), \ldots, s(1, n), s(2, 2), s(2, 3), \ldots, s(2, n), s(3, 3), \ldots, s(n, n)]\)。
例如，如果 \(a = [1, 2, 5, 10]\)，则 \(b = [1, 3, 8, 18, 2, 7, 17, 5, 15, 10]\)。
您有 \(q\) 个查询。在第 \(i\) 个查询期间，您有两个整数 \(l_i\) 和 \(r_i\)，您必须计算 \(\sum_{j=l_i}^{r_i} r_j b_j\)。
输入
第一行包含一个整数 \(n\) (\(1 \leq n \leq 3 \cdot 10^5\))。
第二行包含 \(n\) 个整数 \(a_1, a_2, \ldots, a_n\) (\(-10 \leq a_i \leq 10\))。
第三行包含一个整数 \(q\) (\(1 \leq q \leq 3 \cdot 10^5\))。
接下来是 \(q\) 行，其中第 \(i\) 行包含两个整数 \(l_i\) 和 \(r_i\) (\(1 \leq l_i \leq r_i \leq \frac{n(n+1)}{2}\))。
输出
打印 \(q\) 个整数，其中第 \(i\) 个应等于 \(\sum_{j=l_i}^{r_i} r_j b_j\)。
示例
输入
4
1 2 5 10
15
1 1
1 2
1 3
1 4
1 5
1 10
5 10
6 10
2 8
3 4
3 10
3 8
5 6
5 5
1 8
输出
1
4
12
30
32
86
56
54
60
26
82
57
9
2
61
解题思路
对于题目给出的序列\(b\)，我们可以再构建\(n\)个分区将序列\(b\)进行划分。
其中\(分区i=[\text{s}(i,i),\text{s}(i,i+1),\text{s}(i,i+2),\dots,\text{s}(i,n)]\)
每个分区长度\(\text{len}_i=n-i+1\)
对于第\(i\)个分区，它的分区和\(\text{val}_i=\sum_{j=i}^{n}\text{pre}_j-\text{len}_i\times\text{pre}_{i-1}\)，其中\(\text{pre}_j=\sum_{i=1}^ja_i\)
对于每个查询\([l,r]\)，我们实际可以先求出\(\text{preb}_{l-1}= \sum_{i=1}^{l-1}b_i\)和\(\text{preb}_{r}= \sum_{i=1}^{r}b_i\)，答案则为\(\text{preb}_r-\text{preb}_{l-1}\)
而\(\text{preb}_p=\sum_{i=1}^{j}\text{val}_i+\sum_{k=j+1}^{ p-\text{pos}_j+j}-(p-\text{}pos_j)\times pre_j\)，其中\(j\)为在\(p\)之前的最大完整分区编号，\(pos_j\)为分区\(j\)的结束位置
对于\(j\)我们可以二分求出，\(pos\)则可以根据\(len\)求。
时间复杂度为\(O(n+q\log n)\)
代码实现
void solve()
{
ll n;
cin >> n;
vl a(n + 1);
vl pre(n + 1); // 前缀和
vl pre_pre(n + 1); // 前缀和的前缀和
vl pos(n + 1); // 存储分区i的结束位置
for (int i = 1; i <= n; i++)
{
cin >> a[i];
pre[i] = pre[i - 1] + a[i];
pre_pre[i] = pre_pre[i - 1] + pre[i];
pos[i] = n - i + 1; // 第i个分区长度为 n - i + 1
pos[i] += pos[i - 1];
}
vl pre_val(n + 1); // 存储每个分区值的前缀和
for (ll i = 1; i <= n; i++)
{
pre_val[i] = pre_pre[n] - pre_pre[i - 1] - (n - i + 1) * (pre[i - 1]);
pre_val[i] += pre_val[i - 1];
}
auto query = [&](ll p) -> ll
{
if (p == 0)
return 0;
// 二分查找，找到最大的 l 使得 pos[l] <= p,查找到最大完整分区编号
ll l = 0, r = n + 1;
while (r - l > 1)
{
ll mid = l + r >> 1;
if (pos[mid] <= p)
l = mid;
else
r = mid;
}
ll ans = pre_val[l]; // 将前缀分区和加入答案
// 枚举不完整分区
p -= pos[l] - l;
// 计算不完整分区区间和
ans += pre_pre[p] - pre_pre[l] - (p - l) * (pre[l]);
return ans;
};
ll q;
cin >> q;
while (q-- > 0)
{
ll l, r;
cin >> l >> r;
cout << query(r) - query(l - 1) << '\n';
}
}
E. Best Subsequence
给定一个大小为 \(n\) 的整数数组 \(a\)。
我们将数组的值定义为其大小减去数组所有元素按位或中的设置位数。
例如，对于数组 \([1, 0, 1, 2]\)，按位或为 \(3\)（包含 \(2\) 个设置位），数组的值为 \(4 - 2 = 2\)。
您的任务是计算给定数组的某个子序列的最大可能值。
输入
第一行包含一个整数 \(t\) (\(1 \leq t \leq 100\)) — 测试用例的数量。
每个测试用例的第一行包含一个整数 \(n\) (\(1 \leq n \leq 100\))。
每个测试用例的第二行包含 \(n\) 个整数 \(a_1, a_2, \ldots, a_n\) (\(0 \leq a_i < 2^{60}\))。
输出
对于每个测试用例，打印给定数组的某个子序列的最大可能值。
示例
输入
4
3
0 0 0
4
1 0 1 2
1
5
8
7 1 48 14 13 8 7 6
输出
3
2
0
3
解题思路
最大权闭合子图问题
相关博客推荐：
题目大意
给定一个整数数组，选择一个子序列，使其 "值" 最大化。这里 "值" 定义为子序列的长度减去其所有元素按位或后结果中设置位的数量。
建模思路：
- 每选择一个元素，可以增加子序列的长度，但同时可能增加按位或结果中设置位的数量。
- 目标是最大化 \(子序列长度 - 按位或结果的设置位数\)。
- 反向思考，可以最小化选择的元素数以覆盖所有可能设置位，进而最大化 \(n - 元素数\)。
建图
从源点 \(s\) 到每个元素节点 \(i\) 添加容量为 \(1\) 的边，表示每个元素可以被选中一次。
对于每个元素 \(i\)，遍历其二进制表示的每一位 \(j\)：
-
如果第 \(j\) 位为 \(1\)，则从元素节点 \(i\) 到比特位节点 \(n + j\) 添加一条容量为无穷大的边，表示选择元素 \(i\) 可以覆盖第 \(j\) 位。
-
从每个比特位节点 \(n + j\) 到汇点 \(t\) 添加容量为 \(1\) 的边，表示每个位只能被一个元素覆盖。
最大流代表覆盖的比特位的最大数量，因此选中的元素数最少， \(n - 最大流\)即为答案。
代码实现
// Dinic算法求最大流
template <class T>
struct MaxFlow
{
// 内部结构体，表示图中的一条边
struct _Edge
{
int to; // 边的终点
T cap; // 边的容量
_Edge(int to, T cap) : to(to), cap(cap) {} // 边的构造函数
};
int n; // 图中节点的数量
vector<_Edge> e; // 存储所有边
vector<vector<int>> g; // 邻接表，g[u]存储与节点u相连的所有边的索引
vector<int> cur, h; // 当前正在探索的边的指针和节点的高度（层次）
// 默认构造函数
MaxFlow() {}
// 带节点数量的构造函数，初始化图
MaxFlow(int n)
{
init(n);
}
// 初始化图的节点数量，并清空之前的边和邻接表
void init(int n)
{
this->n = n;
e.clear(); // 清空所有边
g.assign(n, {}); // 初始化邻接表，给每个节点分配一个空的边列表
cur.assign(n, 0); // 初始化当前边指针数组为0
h.assign(n, 0); // 初始化高度数组为0
}
// 广度优先搜索，用于构建层次图
bool bfs(int s, int t)
{
h.assign(n, -1); // 将所有节点的高度初始化为-1，表示未访问
queue<int> que; // 创建一个队列用于BFS
h[s] = 0; // 源点的高度设为0
que.push(s); // 将源点入队
while (!que.empty())
{
int u = que.front(); // 取出队头节点
que.pop();
for (int i : g[u]) // 遍历节点u的所有边
{
auto [v, c] = e[i]; // 获取边的终点v和剩余容量c
if (c > 0 && h[v] == -1) // 如果边有剩余容量且v未被访问
{
h[v] = h[u] + 1; // 更新v的高度，即层次
if (v == t)
return true; // 如果到达汇点，层次图已经构建完成
que.push(v); // 将v入队，继续BFS
}
}
}
return false; // 如果无法到达汇点，返回false
}
// 深度优先搜索，用于在层次图中寻找增广路径并进行流量增广
T dfs(int u, int t, T f)
{
if (u == t)
return f; // 到达汇点，返回当前增广的流量f
T r = f; // 剩余需要增广的流量
for (int &i = cur[u]; i < int(g[u].size()); ++i) // 遍历节点u的所有边，从当前边指针开始
{
int j = g[u][i]; // 获取边的索引
auto [v, c] = e[j]; // 获取边的终点v和剩余容量c
if (c > 0 && h[v] == h[u] + 1) // 如果边有剩余容量且v在层次图中的高度是u的高度加1
{
T a = dfs(v, t, min(r, c)); // 递归地尝试增广流量，选择最小的流量
if (a > 0)
{
e[j].cap -= a; // 减少正向边的剩余容量
e[j ^ 1].cap += a; // 增加反向边的剩余容量
r -= a; // 减少需要增广的剩余流量
if (r == 0)
return f; // 如果已经没有剩余流量需要增广，返回
}
}
}
return f - r; // 返回实际增广的流量
}
// 向图中添加一条从u到v的边，并添加对应的反向边
void addEdge(int u, int v, T c)
{
g[u].push_back(e.size()); // 将边的索引添加到u的邻接表中
e.emplace_back(v, c); // 添加正向边
g[v].push_back(e.size()); // 将反向边的索引添加到v的邻接表中
e.emplace_back(u, 0); // 添加反向边，初始容量为0
}
// 计算从源点s到汇点t的最大流
T flow(int s, int t)
{
T ans = 0; // 初始化最大流量为0
while (bfs(s, t)) // 当存在从s到t的增广路径时
{
// 在每次BFS后需要重置当前边指针
// 这是为了防止在DFS过程中重复遍历已经尝试过的边
cur.assign(n, 0);
// 尝试通过DFS增广流量，添加到总流量中
ans += dfs(s, t, numeric_limits<T>::max());
}
return ans; // 返回最终的最大流量
}
// 计算最小割，返回一个布尔数组，表示每个节点是否在割集的一侧
vector<bool> minCut()
{
vector<bool> c(n);
for (int i = 0; i < n; i++)
c[i] = (h[i] != -1); // 如果节点i的高度不为-1，表示可达源点侧
return c; // 返回最小割结果
}
// 定义一个边结构体，用于存储边的详细信息
struct Edge
{
int from; // 边的起点
int to; // 边的终点
T cap; // 边的容量
T flow; // 边的流量
};
// 获取所有的边信息
vector<Edge> edges()
{
vector<Edge> a;
for (int i = 0; i < e.size(); i += 2) // 遍历所有正向边
{
Edge x;
x.from = e[i + 1].to; // 反向边的终点作为起点
x.to = e[i].to; // 正向边的终点
x.cap = e[i].cap + e[i + 1].cap; // 总容量为正向边和反向边的容量之和
x.flow = e[i + 1].cap; // 流量等于反向边的容量
a.push_back(x); // 将边添加到结果集中
}
return a; // 返回所有边的信息
}
};
void solve()
{
ll n;
cin >> n;
vl a(n);
for (int i = 0; i < n; i++)
{
cin >> a[i];
}
// 创建一个最大流图，节点总数为n个元素节点 + 60个比特位节点 + 源点和汇点
MaxFlow<int> graph(n + 62);
int s = n + 60; // 定义源点的编号为n + 60
int t = s + 1; // 定义汇点的编号为s + 1
// 为每个元素节点添加边连接到源点，容量为1，表示每个元素最多被选中一次
for (int i = 0; i < n; i++)
{
graph.addEdge(s, i, 1);
for (int j = 0; j < 60; j++) // 遍历每个比特位
{
if (a[i] >> j & 1) // 如果元素a[i]的第j位为1
graph.addEdge(i, n + j, inf); // 从元素节点i到比特位节点(n + j)添加无限容量的边
}
}
// 为每个比特位节点添加边连接到汇点，容量为1，表示每个位只能被一个元素覆盖
for (int j = 0; j < 60; j++)
{
graph.addEdge(n + j, t, 1);
}
// 计算最大流，即可以覆盖的比特位的最大数量
int max_flow = graph.flow(s, t);
// 根据题意，最大子序列的值为n - 被覆盖的比特位数量
int ans = n - max_flow;
cout << ans << "\n"; // 输出答案
}
这场写的太抽象了。
A连续四发wa1，幸好不加罚时，但还是浪费一堆时间。
B没注意数据范围，以为是\(2\times10^5\)，我还在想啥场次这么逆天把1500,1600的题放B的位置，幸好这种类型的dp题写的多，直接搞出来了。
C题一下就想倒着枚举，但是边界问题没想明白，差点红温，于是决定果断放弃，直接先写D。
D不难想，一看就是很典型的题目。
E完全没想到是网络流，乱搞了一下把样例过了，还以为对了，结果wa2。
