Codeforces Round 981 div3 个人题解(A~G)
Codeforces Round 981 div3 个人题解(A~G)
Dashboard - Codeforces Round 981 (Div. 3) - Codeforces
火车头
#define _CRT_SECURE_NO_WARNINGS 1
#include <algorithm>
#include <array>
#include <bitset>
#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <chrono>
#include <fstream>
#include <functional>
#include <iomanip>
#include <iostream>
#include <iterator>
#include <list>
#include <map>
#include <numeric>
#include <queue>
#include <random>
#include <set>
#include <stack>
#include <string>
#include <tuple>
#include <unordered_map>
#include <utility>
#include <vector>
#define ft first
#define sd second
#define yes cout << "yes\n"
#define no cout << "no\n"
#define Yes cout << "Yes\n"
#define No cout << "No\n"
#define YES cout << "YES\n"
#define NO cout << "NO\n"
#define pb push_back
#define eb emplace_back
#define all(x) x.begin(), x.end()
#define all1(x) x.begin() + 1, x.end()
#define unq_all(x) x.erase(unique(all(x)), x.end())
#define unq_all1(x) x.erase(unique(all1(x)), x.end())
#define sort_all(x) sort(all(x))
#define sort1_all(x) sort(all1(x))
#define reverse_all(x) reverse(all(x))
#define reverse1_all(x) reverse(all1(x))
#define inf 0x3f3f3f3f
#define infll 0x3f3f3f3f3f3f3f3fLL
#define RED cout << "\033[91m"
#define GREEN cout << "\033[92m"
#define YELLOW cout << "\033[93m"
#define BLUE cout << "\033[94m"
#define MAGENTA cout << "\033[95m"
#define CYAN cout << "\033[96m"
#define RESET cout << "\033[0m"
// 红色
#define DEBUG1(x) \
RED; \
cout << #x << " : " << x << endl; \
RESET;
// 绿色
#define DEBUG2(x) \
GREEN; \
cout << #x << " : " << x << endl; \
RESET;
// 蓝色
#define DEBUG3(x) \
BLUE; \
cout << #x << " : " << x << endl; \
RESET;
// 品红
#define DEBUG4(x) \
MAGENTA; \
cout << #x << " : " << x << endl; \
RESET;
// 青色
#define DEBUG5(x) \
CYAN; \
cout << #x << " : " << x << endl; \
RESET;
// 黄色
#define DEBUG6(x) \
YELLOW; \
cout << #x << " : " << x << endl; \
RESET;
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef long double ld;
// typedef __int128_t i128;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
typedef pair<ld, ld> pdd;
typedef pair<ll, int> pli;
typedef pair<string, string> pss;
typedef pair<string, int> psi;
typedef pair<string, ll> psl;
typedef tuple<int, int, int> ti3;
typedef tuple<ll, ll, ll> tl3;
typedef tuple<ld, ld, ld> tld3;
typedef vector<bool> vb;
typedef vector<int> vi;
typedef vector<ll> vl;
typedef vector<string> vs;
typedef vector<pii> vpii;
typedef vector<pll> vpll;
typedef vector<pli> vpli;
typedef vector<pss> vpss;
typedef vector<ti3> vti3;
typedef vector<tl3> vtl3;
typedef vector<tld3> vtld3;
typedef vector<vi> vvi;
typedef vector<vl> vvl;
typedef queue<int> qi;
typedef queue<ll> ql;
typedef queue<pii> qpii;
typedef queue<pll> qpll;
typedef queue<psi> qpsi;
typedef queue<psl> qpsl;
typedef priority_queue<int> pqi;
typedef priority_queue<ll> pql;
typedef priority_queue<string> pqs;
typedef priority_queue<pii> pqpii;
typedef priority_queue<psi> pqpsi;
typedef priority_queue<pll> pqpll;
typedef priority_queue<psi> pqpsl;
typedef map<int, int> mii;
typedef map<int, bool> mib;
typedef map<ll, ll> mll;
typedef map<ll, bool> mlb;
typedef map<char, int> mci;
typedef map<char, ll> mcl;
typedef map<char, bool> mcb;
typedef map<string, int> msi;
typedef map<string, ll> msl;
typedef map<int, bool> mib;
typedef unordered_map<int, int> umii;
typedef unordered_map<ll, ll> uml;
typedef unordered_map<char, int> umci;
typedef unordered_map<char, ll> umcl;
typedef unordered_map<string, int> umsi;
typedef unordered_map<string, ll> umsl;
std::mt19937_64 rng(std::chrono::steady_clock::now().time_since_epoch().count());
template <typename T>
inline T read()
{
T x = 0;
int y = 1;
char ch = getchar();
while (ch > '9' || ch < '0')
{
if (ch == '-')
y = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9')
{
x = (x << 3) + (x << 1) + (ch ^ 48);
ch = getchar();
}
return x * y;
}
template <typename T>
inline void write(T x)
{
if (x < 0)
{
putchar('-');
x = -x;
}
if (x >= 10)
{
write(x / 10);
}
putchar(x % 10 + '0');
}
/*#####################################BEGIN#####################################*/
void solve()
{
}
int main()
{
ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0);
// freopen("test.in", "r", stdin);
// freopen("test.out", "w", stdout);
int _ = 1;
std::cin >> _;
while (_--)
{
solve();
}
return 0;
}
/*######################################END######################################*/
// 链接:
A. Sakurako and Kosuke
时间限制:每个测试 1 秒
内存限制:每个测试 256 兆字节
Sakurako 和 Kosuke 决定用坐标线上的一个点来玩一些游戏。这个点目前位于位置 \(x=0\)。他们将轮流行动,Sakurako 将首先行动。
在第 \(i\) 步,当前玩家将把点向某个方向移动 \(2 \cdot i - 1\) 个单位。Sakurako 将始终向负方向移动点,而 Kosuke 将始终向正方向移动点。
换句话说,将会发生以下情况:
- Sakurako 现在将点的位置改变 \(-1\),\(x=-1\) 现在
- Kosuke 现在将点的位置改变 \(3\),\(x=2\) 现在
- Sakurako 现在将点的位置改变 \(-5\),\(x=-3\) 现在
- ⋯
只要点的坐标绝对值不超过 \(n\),他们就会继续玩。更正式地说,游戏在 \(-n \leq x \leq n\) 时继续。可以证明游戏总会结束。
你的任务是确定谁将是最后一个回合的人。
输入
第一行包含一个整数 \(t\) (\(1 \leq t \leq 100\)) — Sakurako 和 Kosuke 玩的游戏数量。
每场游戏都由一个数字 \(n\) (\(1 \leq n \leq 100\)) 描述 — 该数字定义游戏结束时的条件。
输出
对于每个 \(t\) 场游戏,输出一行该游戏的结果。如果 Sakurako 完成了最后一轮,则输出“Sakurako”(不带引号);否则输出“Kosuke”。
示例
输入
4
1
6
3
98
输出
Kosuke
Sakurako
Kosuke
Sakurako
解题思路
观察样例发现,\(|x_i|=i\),第\(i\)个位置的绝对值为\(i\),所以只需要判断奇偶即可,奇数一定是Kosuke最后走,偶数一定是Sakurako最后走。
代码实现
void solve()
{
int n;
cin >> n;
if (n & 1)
cout << "Kosuke\n";
else
cout << "Sakurako\n";
}
B. Sakurako and Water
时间限制:每个测试 2 秒
内存限制:每个测试 256 兆字节
在与小介的旅途中,樱子和小介发现了一个山谷,可以用大小为 \(n \times n\) 的矩阵来表示,其中第 \(i\) 行和 \(j\) 列的交点处是一座山,高度为 \(a_{i,j}\)。如果 \(a_{i,j} < 0\),那么那里有一个湖。
小介非常怕水,所以樱子需要帮助他:
用她的魔法,她可以选择一个正方形的山脉区域,并将该区域主对角线上每座山脉的高度增加一。更正式地说,她可以选择一个子矩阵,其左上角位于 \((i,j)\),右下角位于 \((p,q)\),这样 \(p - i = q - j\)。然后,她可以将所有 \(k\) 的 \((i+k)\) 行和 \((j+k)\) 列交叉处的每个元素加一,使得 \(0 \leq k \leq p - i\)。
已知山谷中每个点的高度都小于 0。
确定樱子必须使用魔法的最少次数,以使每个尖峰的高度变为非负值。
输入
第一行包含一个整数 \(t\) (\(1 \leq t \leq 200\)) — 测试用例的数量。
每个测试用例的描述如下:
每个测试用例的第一行由一个数字 \(n\) (\(1 \leq n \leq 500\)) 组成。
接下来的每一行 \(n\) 都由空格分隔的 \(n\) 个整数组成,这些整数对应于矩阵 \(a\) (\(-10^5 \leq a_{i,j} \leq 10^5\)) 中尖峰的高度。
保证所有测试用例的 \(n\) 之和不超过 1000。
输出
对于每个测试用例,输出樱子必须使用魔法的最少次数,以使所有湖泊消失。
示例
输入
4
1
1
2
-1 2
3 0
3
1 2 3
-2 1 -1
0 0 -1
5
1 1 -1 -1 3
-3 1 4 4 -4
-1 -1 3 0 -5
4 5 3 -3 -1
3 1 -3 -1 5
输出
0
1
4
19
解题思路
如果要使得总操作次数最少,选取的正方形一定是越大越好,这样覆盖的可以修改的主对角线山峰才越多。
所有我们每次选择一定是选择可以选的最长主对角线。
如果要使得一整条主对角线上的所有山峰大于等于\(0\),那么至少需要加上这条主对角上小于\(0\)的最小峰的绝对值。
所以我们只需枚举正方形山谷的所有主对角线,找到每条主对角线的小于\(0\)最小值,把它们的绝对值加起来即可。
下图为样例3的所有主对角线(颜色相同的在同一主对角线上)
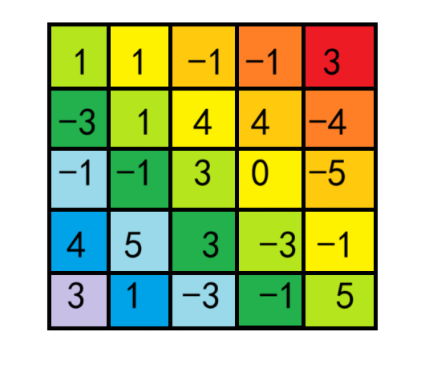
代码实现
void solve()
{
int n;
cin >> n;
vvl a(n, vl(n));
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
cin >> a[i][j];
}
}
ll ans = 0;
for (int i = 0; i < n; i++)
{
i64 mn = a[0][i];
int x = 0, y = i;
while (x < n && y < n)
{
mn = min(mn, a[x][y]);
x++;
y++;
}
if (mn < 0)
{
// cout << mn << endl;
ans += mn;
}
}
for (int j = 1; j < n; j++)
{
ll mn = a[j][0];
int x = j, y = 0;
while (x < n && y < n)
{
mn = min(mn, a[x][y]);
x++;
y++;
}
if (mn < 0)
{
// cout << mn << endl;
ans += mn;
}
}
cout << -ans << endl;
}
C. Sakurako's Field Trip
时间限制:每个测试 2 秒
内存限制:每个测试 256 兆字节
即使在大学里,学生也需要放松。这就是 Sakurako 老师决定去实地考察的原因。众所周知,所有学生都会排成一排。索引为 \(i\) 的学生有一些感兴趣的话题,描述为 \(a_i\)。作为一名老师,您希望尽量减少学生队伍的干扰。
队伍的干扰定义为具有相同兴趣话题的邻近人数。换句话说,干扰是索引 \(j\) (\(1 \leq j < n\)) 的数量,例如 \(a_j = a_{j+1}\)。
为了做到这一点,您可以选择索引 \(i\) (\(1 \leq i \leq n\)) 并交换位置 \(i\) 和 \(n - i + 1\) 的学生。您可以执行任意数量的交换。
您的任务是确定通过多次执行上述操作可以实现的最小干扰量。
输入
第一行包含一个整数 \(t\) (\(1 \leq t \leq 10^4\)) — 测试用例的数量。
每个测试用例用两行描述。
第一行包含一个整数 \(n\) (\(2 \leq n \leq 10^5\)) — 学生队伍的长度。
第二行包含 \(n\) 个整数 \(a_i\) (\(1 \leq a_i \leq n\)) — 队伍中学生感兴趣的主题。
保证所有测试用例的 \(n\) 之和不超过 \(2 \cdot 10^5\)。
输出
对于每个测试用例,输出您可以实现的线路的最小可能干扰。
示例
输入
9
5
1 1 1 2 3
6
2 1 2 2 1 1
4
1 2 1 1
6
2 1 1 2 2 4
4
2 1 2 3
6
1 2 2 1 2 1
5
4 5 5 1 5
7
1 4 3 5 1 1 3
7
3 1 3 2 2 3 3
输出
1
2
1
0
0
1
1
0
2
说明
在第一个示例中,需要对 \(i=2\) 进行操作,因此数组将变为 \([1,2,1,1,3]\),其中粗体元素表示已交换的位置。该数组的干扰量等于 1。
在第四个示例中,只需对 \(i=3\) 进行操作,因此数组将变为 \([2,1,2,1,2,4]\)。该数组的干扰量等于 0。
在第八个示例中,只需对 \(i=3\) 进行操作,因此数组将变为 \([1,4,1,5,3,1,3]\)。该数组的干扰量等于 0。
解题思路
对于每个位置,统计一下不交换时的干扰\(pre\)和假如交换后的干扰\(nex\),如果\(nex<pre\),直接进行交换。
代码实现
void solve()
{
int n;
cin >> n;
vi a(n + 1);
for (int i = 1; i <= n; i++)
{
cin >> a[i];
}
for (int i = 2; i <= n / 2; i++)
{
int pre = (a[i] == a[i - 1]) + (a[n - i + 1] == a[n - i + 2]);
int nex = (a[i] == a[n - i + 2]) + (a[n - i + 1] == a[i - 1]);
if (nex < pre)
swap(a[i], a[n - i + 1]);
}
int ans = 0;
for (int i = 2; i <= n; i++)
{
if (a[i] == a[i - 1])
ans++;
}
cout << ans << "\n";
}
D. Kousuke's Assignment
时间限制:每个测试 2 秒
内存限制:每个测试 256 兆字节
在和 Sakurako 一起旅行后,Kousuke 非常害怕,因为他忘记了他的编程作业。在这次作业中,老师给了他一个包含 \(n\) 个整数的数组 \(a\),并要求他计算数组 \(a\) 中不重叠线段的数量,使得每个线段都被认为是美丽的。
如果线段 \([l,r]\) 满足 \(a_l + a_{l+1} + \cdots + a_{r-1} + a_r = 0\),则该线段被认为是美丽的。
对于固定数组 \(a\),您的任务是计算不重叠的美丽线段的最大数量。
输入
输入的第一行包含数字 \(t\) (\(1 \leq t \leq 10^4\)) — 测试用例的数量。每个测试用例由 2 行组成。
第一行包含一个整数 \(n\) (\(1 \leq n \leq 10^5\)) — 数组的长度。
第二行包含 \(n\) 个整数 \(a_i\) (\(-10^5 \leq a_i \leq 10^5\)) — 数组 \(a\) 的元素。
保证所有测试用例的 \(n\) 的总和不超过 \(3 \cdot 10^5\)。
输出
对于每个测试用例,输出一个整数:不重叠的美丽线段的最大数量。
示例
输入
3
5
2 1 -3 2 1
7
12 -4 4 43 -3 -5 8
6
0 -4 0 3 0 1
输出
1
2
3
解题思路
前缀和的板子题,对于数组\(a\),我们计算出它的前缀和\(pre\)。对于每个前缀和,我们维护上一个下标。
如果遇见相同的前缀和,查询该前缀和的上一个下标是否小于上一段线段的结束位置。
如果小于则选择,否则更新该前缀和的上一个下标。
代码实现
void solve()
{
int n;
cin >> n;
vl a(n);
for (int i = 0; i < n; i++)
{
cin >> a[i];
}
mll mp;
ll sum = 0;
mp[0] = -1;
int cnt = 0;
int last = -1;
for (int i = 0; i < n; i++)
{
sum += a[i];
if (mp.find(sum) != mp.end())
{
int p = mp[sum];
if (p >= last)
{
cnt++;
last = i;
}
}
mp[sum] = i;
}
cout << cnt << "\n";
}
E. Sakurako, Kosuke, and the Permutation
时间限制:每个测试 2 秒
内存限制:每个测试 256 兆字节
Sakurako 的考试结束了,她表现非常出色。作为奖励,她得到了一个排列 \(p\)。Kosuke 并不完全满意,因为他有一次考试不及格,而且没有收到礼物。他决定潜入她的房间(多亏了她锁的密码)并破坏排列,使其变得简单。
如果对于每个 \(i\) (\(1 \leq i \leq n\)) 满足以下条件之一,则排列 \(p\) 被认为是简单的:
- \(p_i = i\)
- \(p_{p_i} = i\)
例如,排列 \([1,2,3,4]\)、\([5,2,4,3,1]\) 和 \([2,1]\) 是简单的,而 \([2,3,1]\) 和 \([5,2,1,4,3]\) 则不是。
在一次操作中,Kosuke 可以选择索引 \(i,j\) (\(1 \leq i,j \leq n\)) 并交换元素 \(p_i\) 和 \(p_j\)。
Sakurako 即将回家。您的任务是计算 Kosuke 需要执行的最少操作数,以使排列变得简单。
输入
第一行包含一个整数 \(t\) (\(1 \leq t \leq 10^4\)) — 测试用例的数量。
每个测试用例用两行描述。
第一行包含一个整数 \(n\) (\(1 \leq n \leq 10^6\)) — 排列 \(p\) 的长度。
第二行包含 \(n\) 个整数 \(p_i\) (\(1 \leq p_i \leq n\)) — 排列 \(p\) 的元素。
保证所有测试用例的 \(n\) 之和不超过 \(10^6\)。
输出
对于每个测试用例,输出 Kosuke 需要执行的最少操作数,以使排列变得简单。
示例
输入
6
5
1 2 3 4 5
5
5 4 3 2 1
5
2 3 4 5 1
4
2 3 4 1
3
1 3 2
7
2 3 1 5 6 7 4
输出
0
0
2
1
0
2
说明
在第一个和第二个示例中,排列已经很简单。
在第四个示例中,只需交换 \(p_2\) 和 \(p_4\) 即可。因此,在 1 次操作中,排列将变为 \([2,1,4,3]\)。解题思路
解题思路
我们称\(i\rightarrow p_i \rightarrow p_{p_i} \rightarrow p_{p_{p_i}}\rightarrow \dots \rightarrow i\)为一个循环节,观察发现,对于一个循环节来说,我们只需要操作\(\lfloor \frac{ \text{size}-1}{2} \rfloor\)(size为循环节大小)次,就可以把循环节拆成size小于2。
如图
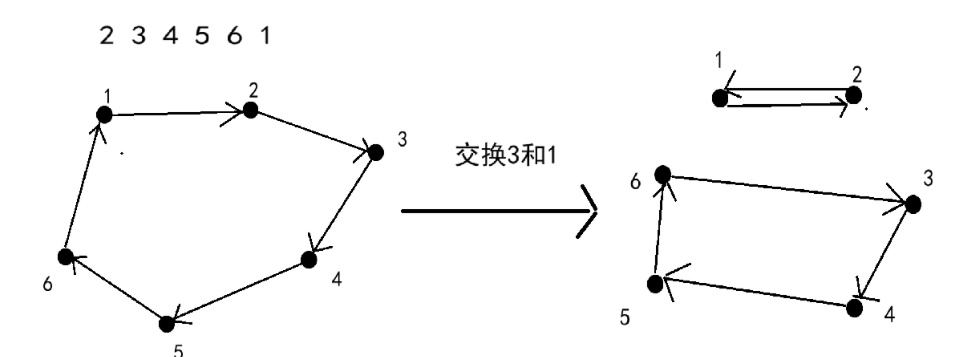
所以我们只需使用并查集缩点,然后枚举所有联通块,计算\(\lfloor \frac{ \text{size}-1}{2} \rfloor\)之和即可。
感觉这题的难度远小于C
代码实现
struct DSU
{
vector<int> f; // 存储父节点
vector<int> siz; // 存储每个集合的大小
// 默认构造函数
DSU() {}
// 构造函数,初始化并查集
DSU(int n)
{
init(n);
}
// 初始化并查集
void init(int n)
{
f.resize(n + 1); // 调整父节点数组大小
iota(f.begin(), f.end(), 0); // 将父节点初始化为自身
siz.assign(n + 1, 1); // 每个集合初始大小为 1
}
// 查找操作,返回 x 的根节点
int find(int x)
{
// 路径压缩
while (x != f[x])
{
// 将 x 的父节点直接指向其祖父节点
x = f[x] = f[f[x]];
}
return x; // 返回根节点
}
// 判断 x 和 y 是否在同一个集合中
bool same(int x, int y)
{
return find(x) == find(y); // 如果根节点相同,则在同一个集合
}
// 合并操作,将 x 和 y 所在的集合合并
bool merge(int x, int y)
{
x = find(x); // 找到 x 的根节点
y = find(y); // 找到 y 的根节点
if (x == y)
{
return false; // 如果已经在同一集合,返回 false
}
// 按秩合并,将较小的集合合并到较大的集合中
if (siz[x] < siz[y])
swap(x, y);
siz[x] += siz[y]; // 更新集合大小
f[y] = x; // 将 y 的根节点指向 x
return true; // 返回 true 表示合并成功
}
// 返回 x 所在集合的大小
int size(int x)
{
return siz[find(x)]; // 返回根节点对应的集合大小
}
};
void solve()
{
int n;
cin >> n;
DSU dsu(n);
for (int i = 1; i <= n; i++)
{
int x;
cin >> x;
dsu.merge(i, x);
}
vb vis(n + 1);
int ans = 0;
for (int i = 1; i <= n; i++)
{
int pa = dsu.find(i);
if (vis[pa])
continue;
vis[pa] = true;
int sz = dsu.size(pa);
if (sz == 1 || sz == 2)
continue;
ans += (sz - 1) / 2;
}
cout << ans << endl;
}
F. Kosuke's Sloth
**### F. Kosuke 的懒惰
时间限制:每个测试 1 秒
内存限制:每个测试 256 兆字节
Kosuke 太懒了。他不会给你任何图例,只会给你任务:
斐波那契数定义如下:
- $ f(1) = f(2) = 1 $
- $ f(n) = f(n-1) + f(n-2) $ (当 $ n \geq 3 $ 时)
我们将 $ G(n,k) $ 表示为第 $ n $ 个斐波那契数的索引,该数可被 $ k $ 整除。对于给定的 $ n $ 和 $ k $,计算 $ G(n,k) $。
由于这个数字可能太大,因此将其以模数 $ 10^9 + 7 $ 输出。
例如:$ G(3,2) = 9 $,因为能被 2 整除的第 3 个斐波那契数是 34。序列为 [1, 1, 2, 3, 5, 8, 13, 21, 34]。
输入
输入数据的第一行包含一个整数 $ t $ (\(1 \leq t \leq 10^4\)) — 测试用例的数量。
第一行也是唯一一行包含两个整数 $ n $ 和 $ k $ (\(1 \leq n \leq 10^{18}\), \(1 \leq k \leq 10^5\))。
保证所有测试用例的 $ k $ 之和不超过 $ 10^6 $。
输出
对于每个测试用例,输出唯一的数字:模数为 $ 10^9 + 7 $ 后得到的值 $ G(n,k) $。
示例
输入
3
3 2
100 1
1000000000000 1377
输出
9
100
999244007
解题思路
由皮亚诺定理可知,模数为\(k\)的循环节长度不会超过\(6k\),所以我们可以暴力枚举找到第一个\(k\)的倍数的位置\(p\),答案即为\(pn\)
时间复杂度复杂度\(O(m)\)
相关证明:
Pisano Period - Shiina_Mashiro - 博客园
代码实现
const ll mod = 1e9 + 7;
const int N = 1e6 + 5;
int f[N];
void solve()
{
ll n;
cin >> n;
int m;
cin >> m;
f[1] = 1;
f[2] = 1;
ll p = 0;
int i = 3;
while (1)
{
f[i] = (f[i - 1] + f[i - 2]) % m;
if (!f[i])
{
p = i;
break;
}
i++;
}
if (m == 1)
p = 1;
cout << (n % mod) * (p % mod) % mod << "\n";
}
G. Sakurako and Chefir
时间限制:每个测试 4 秒
内存限制:每个测试 256 兆字节
给定一棵树,其顶点有 $ n $ 个,根节点为顶点 1。当 Sakurako 带着她的猫 Chefir 穿过这棵树时,她分心了,Chefir 跑掉了。
为了帮助 Sakurako,Kosuke 记录了他的 $ q $ 个猜测。在第 $ i $ 个猜测中,他假设 Chefir 在顶点 $ v_i $ 处迷路了,并且有 $ k_i $ 的体力。
此外,对于每个猜测,Kosuke 假设 Chefir 可以沿边移动任意次数:
- 从顶点 $ a $ 到顶点 $ b $,如果 $ a $ 是 $ b $ 的祖先,则耐力不会改变;
- 从顶点 $ a $ 到顶点 $ b $,如果 $ a $ 不是 $ b $ 的祖先,则 Chefir 的耐力会减少 1;
- 如果 Chefir 的耐力为 0,则他无法进行第二种类型的移动。
对于每个假设,您的任务是找出 Chefir 从顶点 $ v_i $ 到达最远顶点的距离,并且具有 $ k_i $ 的耐力。
输入
第一行包含一个整数 $ t $ (\(1 \leq t \leq 10^4\)) — 测试用例的数量。
每个测试用例描述如下:
第一行包含一个整数 $ n $ (\(2 \leq n \leq 2 \cdot 10^5\)) — 树中的顶点数量。
接下来的 $ n-1 $ 行包含树的边。保证给定的边形成一棵树。
下一行由一个整数 $ q $ (\(1 \leq q \leq 2 \cdot 10^5\)) 组成,表示 Kosuke 的猜测次数。
接下来的 $ q $ 行描述了 Kosuke 的猜测,其中有两个整数 $ v_i \(、\) k_i $ (\(1 \leq v_i \leq n\), \(0 \leq k_i \leq n\))。
保证所有测试用例的 $ n $ 与 $ q $ 之和不超过 $ 2 \cdot 10^5 $。
输出
对于每个测试用例和每个猜测,输出 Chefir 从具有 $ k_i $ 耐力的起点 $ v_i $ 到最远顶点的最大距离。
示例
输入
3
5
1 2
2 3
3 4
3 5
3
5 1
3 1
2 0
9
8 1
1 7
1 4
7 3
4 9
3 2
1 5
3 6
7
6 0
2 3
6 2
8 2
2 4
9 2
6 3
6
2 1
2 5
2 4
5 6
4 3
3
3 1
1 3
6 5
输出
2
1
2
0
5
2
4
5
5
5
1
3
4
说明
在第一个示例中:
- 在第一个查询中,您可以从顶点 5 到顶点 3(耐力减少 1 并变为 0),然后可以到达顶点 4;
- 在第二个查询中,从顶点 3 具有 1 点耐力,您只能到达顶点 2、3、4 和 5;
- 在第三个查询中,从顶点 2 具有 0 点耐力,您只能到达顶点 2、3、4 和 5。
解题思路
观察发现,第一种行动实际上就是沿着树向下走,第二种行动就是沿着树向上走。
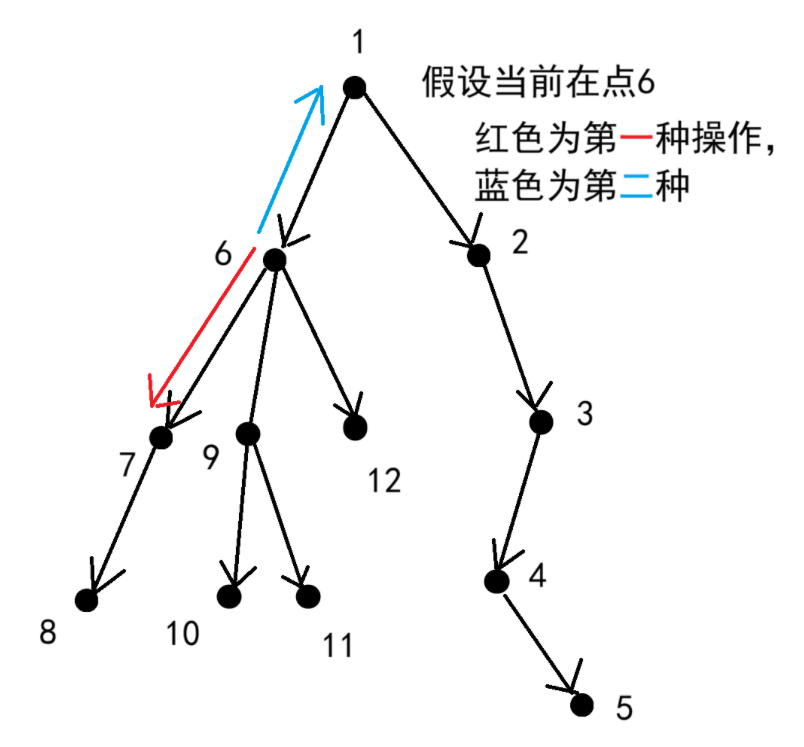
所以对于一个节点来说,我们一定可以一直使用第一种操作走到这个节点的最深子叶子节点。
对于每一个节点,我们可以使用dfs计算出每个节点的最深子叶子节点到当前节点的距离maxDep
那么一个节点可以走到的最远距离即为\(\max\{\text{maxDep}_{u+i}+i\},0\le i \le k\)
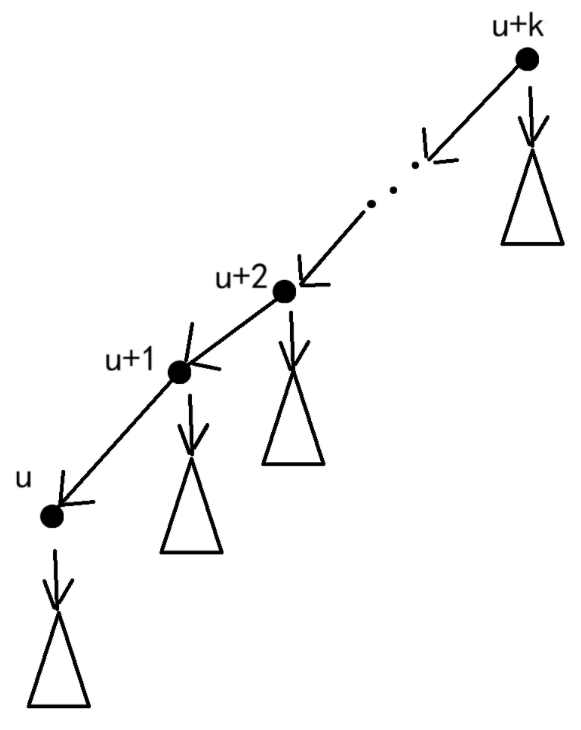
考虑暴力的做法,对于每一次询问,我们对于节点\(v\)向上查询\(k\)个父节点,找到\(\max\{\text{maxDep}_{u+i}+i\}\)
单次询问时间复杂多为\(O(k)\),如果数据保证随机,总时间复杂度为\(O(qlogn)\),但可惜不是。遇到链的情况会使得时间复杂度退化到\(O(qk)\),一定会超时,所以考虑优化。
我们使用dfs计算出每个节点的深度\(dep\),发现对于在树的一条链上的所有询问,我们实际上寻找的就是区间\([dep_v,dep_{v-k}]\)的最大\(maxDep\)。
所以我们可以把询问离线出来,对于树的每一条链,构建一下线段树,存储区间最大\(maxDep\)。
然后dfs遍历所有节点,如果发现当前节点存在询问,直接在线段树中进行查询。
为了节省空间,我们再遍历完一条树的链之后,可以在递归回溯是重置一下当前节点在线段树中的值,这样只需要一棵线段树即可。
实际复杂度为\(O(nlogn)\)
代码实现
// 懒标记线段树模板类
template <class Info, class Tag>
struct LazySegmentTree
{
const int n; // 数组大小
std::vector<Info> info; // 存储线段树节点的信息
std::vector<Tag> tag; // 存储懒标记
// 构造函数
LazySegmentTree(int n) : n(n), info(4 << std::__lg(n)), tag(4 << std::__lg(n)) {}
// 用于初始化线段树的构造函数
LazySegmentTree(std::vector<Info> init) : LazySegmentTree(init.size())
{
std::function<void(int, int, int)> build = [&](int p, int l, int r)
{
if (r - l == 1)
{
info[p] = init[l]; // 叶子节点赋值
return;
}
int m = (l + r) / 2; // 中间点
build(2 * p, l, m); // 构建左子树
build(2 * p + 1, m, r); // 构建右子树
pull(p); // 更新父节点
};
build(1, 0, n);
}
// 更新父节点
void pull(int p)
{
info[p] = info[2 * p] + info[2 * p + 1]; // 合并左右子树的信息
}
// 应用标签到节点
void apply(int p, const Tag &v)
{
info[p].apply(v); // 应用标签到信息
tag[p].apply(v); // 更新懒标记
}
// 推送懒标记到子节点
void push(int p)
{
apply(2 * p, tag[p]); // 推送到左子树
apply(2 * p + 1, tag[p]); // 推送到右子树
tag[p] = Tag(); // 清空当前节点的懒标记
}
// 修改某个位置的值
void modify(int p, int l, int r, int x, const Info &v)
{
if (r - l == 1)
{
info[p] = v; // 更新叶子节点
return;
}
int m = (l + r) / 2; // 中间点
push(p); // 推送懒标记
if (x < m)
{
modify(2 * p, l, m, x, v); // 递归到左子树
}
else
{
modify(2 * p + 1, m, r, x, v); // 递归到右子树
}
pull(p); // 更新父节点
}
// 对外接口,修改某个位置的值
void modify(int p, const Info &v)
{
modify(1, 0, n, p, v);
}
// 区间查询
Info rangeQuery(int p, int l, int r, int x, int y)
{
if (l >= y || r <= x)
{
return Info(); // 范围不相交,返回默认信息
}
if (l >= x && r <= y)
{
return info[p]; // 当前区间完全包含在查询范围内
}
int m = (l + r) / 2; // 中间点
push(p); // 推送懒标记
return rangeQuery(2 * p, l, m, x, y) + rangeQuery(2 * p + 1, m, r, x, y);
}
// 对外接口,区间查询
Info rangeQuery(int l, int r)
{
return rangeQuery(1, 0, n, l, r);
}
};
// 标签结构
struct Tag
{
int change = -inf; // 增加的值
// 应用标签的操作
void apply(Tag t) &
{
change = t.change; // 累加增加的值
}
};
// 信息结构
struct Info
{
int max = -inf;
void apply(Tag t) &
{
if (t.change != -inf)
{
max = t.change; // 更新最大值
}
}
Info() {};
Info(int x) : max(x) {}
};
// 信息结构的加法运算符重载
Info operator+(Info a, Info b)
{
Info c;
c.max = max(a.max, b.max);
return c;
}
// 查询结构体
struct Query
{
int k;
int id;
Query(int k_, int id_) : k(k_), id(id_) {}
};
void solve()
{
int n;
cin >> n;
vvi adj(n + 1);
for (int i = 1; i < n; i++)
{
int u, v;
cin >> u >> v;
adj[u].pb(v);
adj[v].pb(u);
}
vi dep(n + 1); // 存储每个节点的深度
vi maxDep(n + 1); // 存储每个节点可以向下走的最大深度
// 深度优先搜索 (DFS) 函数,用于计算每个节点的深度和最大深度
function<void(int, int)> dfs1 = [&](int u, int fa)
{
maxDep[u] = 0;
for (auto v : adj[u])
{
if (v == fa) // 如果 v 是父节点,跳过
continue;
dep[v] = dep[u] + 1;
dfs1(v, u);
maxDep[u] = max(maxDep[u], maxDep[v] + 1);
}
};
dfs1(1, 0);
int m;
cin >> m;
vector<vector<Query>> querys(n + 1);
vi ans(m);
for (int i = 0; i < m; i++)
{
int v, k;
cin >> v >> k;
querys[v].pb({k, i});
}
// 创建线段树
LazySegmentTree<Info, Tag> seg(n);
// 处理查询
function<void(int, int)> dfs2 = [&](int u, int fa)
{
// 处理当前节点 u 的所有查询
for (auto &q : querys[u])
{
int k = q.k, id = q.id;
ans[id] = max(ans[id], maxDep[u]); // 更新答案为当前节点的最大深度
// 通过线段树查询从 可到达最浅深度dep[u] - k 到 dep[u] 的最大值,并加上 dep[u]
ans[id] = max(ans[id], seg.rangeQuery(max(0, dep[u] - k), dep[u]).max + dep[u]);
}
// 找到当前节点 u 的子节点中最大和次大子树深度
int max1 = 0, max2 = 0;
for (auto v : adj[u])
{
if (v == fa)
continue;
if (maxDep[v] + 1 > max1)
{
max2 = max1;
max1 = maxDep[v] + 1;
}
else if (maxDep[v] + 1 > max2)
{
max2 = maxDep[v] + 1;
}
}
// 递归处理每个子节点
for (auto v : adj[u])
{
if (v == fa)
continue;
// 如果当前子节点的最大深度 + 1 等于 max1,说明最大子树深度就是maxDep[v],不能重复选,选次大子树深度
int d = maxDep[v] + 1 == max1 ? max2 : max1;
seg.modify(dep[u], Info(d - dep[u])); // 在线段树中添加走到u节点可向下走的最大深度
dfs2(v, u);
seg.modify(dep[u], -inf); // 回溯时重置线段树中的值
}
};
dfs2(1, 0);
for (int i = 0; i < m; i++)
{
cout << ans[i] << " \n"[i == m - 1];
}
}
早知道大号多掉点分了,这场用小号打的。



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 地球OL攻略 —— 某应届生求职总结
· 周边上新:园子的第一款马克杯温暖上架
· Open-Sora 2.0 重磅开源!
· 提示词工程——AI应用必不可少的技术
· .NET周刊【3月第1期 2025-03-02】