Educational Codeforces Round 166 个人题解(A~D)
Educational Codeforces Round 166 (Rated for Div. 2)个人题解
题解火车头
#define _CRT_SECURE_NO_WARNINGS 1
#include <iostream>
#include <vector>
#include <algorithm>
#include <set>
#include <unordered_map>
#include <cstring>
#include <cstdio>
#include <string>
#include <queue>
#include <stack>
#include <map>
#include <list>
#include <bitset>
#include <cmath>
#include <numeric>
#define endl '\n'
#define ft first
#define sd second
#define yes cout << "yes\n"
#define no cout << "no\n"
#define Yes cout << "Yes\n"
#define No cout << "No\n"
#define YES cout << "YES\n"
#define NO cout << "NO\n"
#define pb push_back
#define eb emplace_back
#define all(x) x.begin(), x.end()
#define unq_all(x) x.erase(unique(all(x)), x.end())
#define sort_all(x) sort(all(x))
#define reverse_all(x) reverse(all(x))
#define INF 0x7fffffff
#define INFLL 0x7fffffffffffffffLL
#define RED cout << "\033[91m"
#define GREEN cout << "\033[92m"
#define YELLOW cout << "\033[93m"
#define BLUE cout << "\033[94m"
#define MAGENTA cout << "\033[95m"
#define CYAN cout << "\033[96m"
#define RESET cout << "\033[0m"
// 红色
#define DEBUG1(x) \
RED; \
cout << #x << " : " << x << endl; \
RESET;
// 绿色
#define DEBUG2(x) \
GREEN; \
cout << #x << " : " << x << endl; \
RESET;
// 蓝色
#define DEBUG3(x) \
BLUE; \
cout << #x << " : " << x << endl; \
RESET;
// 品红
#define DEBUG4(x) \
MAGENTA; \
cout << #x << " : " << x << endl; \
RESET;
// 青色
#define DEBUG5(x) \
CYAN; \
cout << #x << " : " << x << endl; \
RESET;
// 黄色
#define DEBUG6(x) \
YELLOW; \
cout << #x << " : " << x << endl; \
RESET;
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef long double ld;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
typedef pair<ld, ld> pdd;
typedef pair<string, string> pss;
typedef pair<string, int> psi;
typedef pair<string, ll> psl;
typedef vector<bool> vb;
typedef vector<int> vi;
typedef vector<ll> vl;
typedef vector<string> vs;
typedef vector<pii> vpii;
typedef vector<pll> vpll;
typedef vector<pss> vpss;
typedef vector<vi> vvi;
typedef vector<vl> vvl;
typedef queue<int> qi;
typedef queue<ll> ql;
typedef queue<pii> qpii;
typedef queue<pll> qpll;
typedef queue<psi> qpsi;
typedef queue<psl> qpsl;
typedef priority_queue<int> pqi;
typedef priority_queue<ll> pql;
typedef priority_queue<string> pqs;
typedef priority_queue<pii> pqpii;
typedef priority_queue<psi> pqpsi;
typedef priority_queue<pll> pqpl;
typedef priority_queue<psi> pqpsl;
typedef map<int, int> mii;
typedef map<int, bool> mib;
typedef map<ll, ll> mll;
typedef map<ll, bool> mlb;
typedef map<char, int> mci;
typedef map<char, ll> mcl;
typedef map<char, bool> mcb;
typedef map<string, int> msi;
typedef map<string, ll> msl;
typedef map<int, bool> mib;
typedef unordered_map<int, int> umii;
typedef unordered_map<ll, ll> uml;
typedef unordered_map<char, int> umci;
typedef unordered_map<char, ll> umcl;
typedef unordered_map<string, int> umsi;
typedef unordered_map<string, ll> umsl;
template <typename T>
inline void read(T &x)
{
T f = 1;
x = 0;
char ch = getchar();
while (0 == isdigit(ch))
{
if (ch == '-')
f = -1;
ch = getchar();
}
while (0 != isdigit(ch))
x = (x << 1) + (x << 3) + ch - '0', ch = getchar();
x *= f;
}
template <typename T>
inline void write(T x)
{
if (x < 0)
{
x = ~(x - 1);
putchar('-');
}
if (x > 9)
write(x / 10);
putchar(x % 10 + '0');
}
Problem - 1976A - Codeforces
A. 验证密码
每个测试的时间限制：2秒
每个测试的内存限制：256兆字节
输入：标准输入
输出：标准输出
Monocarp 正在开发他的新网站，目前面临的挑战是如何让用户选择强密码。
Monocarp 认为，强密码应满足以下条件：
- 密码只能由小写拉丁字母和数字组成；
- 字母后面不能有数字（因此，每个字母后面要么有另一个字母，要么字符串结束）；
- 所有数字应按非递减顺序排序；
- 所有字母应按非递减顺序排序。
请注意，密码可以只有字母或只有数字。
Monocarp 成功地实现了第一个条件，但他在其余条件上很吃力。您能帮他验证密码吗？
输入
第一行包含一个整数 \(t\) \((1 \leq t \leq 1000)\) — 测试用例的数量。
每个测试用例的第一行包含一个整数 \(n\) \((1 \leq n \leq 20)\) — 密码的长度。
第二行包含一个字符串，正好由 \(n\) 个字符组成。每个字符都是小写拉丁字母或数字。
输出
对于每个测试用例，如果给定的密码很强，则打印“YES”，否则打印“NO”。
示例
输入
5
4
12ac
5
123wa
9
allllmost
5
ac123
6
011679
输出
YES
NO
YES
NO
YES
注
在第二个测试用例中，字母没有按非递减顺序排序。
在第四个测试用例中，字母后面有一个数字 —— 字母 'c' 后面是数字 '1'。
解题思路
查找是否存在\(a1\)这样前面为字母后面为数字的字段和前面大，后面小的字段就行
题解
void solve()
{
int n;
cin >> n;
string s;
cin >> s;
bool flag = true;
for (int i = 1; i < n; i++)
{
if (isalpha(s[i - 1]) && isdigit(s[i]))
{
flag = false;
break;
}
if (s[i - 1] > s[i])
{
flag = false;
break;
}
}
if (flag)
YES;
else
NO;
}
int main()
{
ios::sync_with_stdio(false), std::cin.tie(nullptr), std::cout.tie(nullptr);
int _ = 1;
std::cin >> _;
while (_--)
{
solve();
}
return 0;
}
Problem - 1976B - Codeforces
B. 增加/减少/复制
每个测试的时间限制：2秒
每个测试的内存限制：256兆字节
输入：标准输入
输出：标准输出
给你两个整数数组：长度为 \(n\) 的数组 \(a\) 和长度为 \(n+1\) 的数组 \(b\)。
你可以按任意顺序多次执行下列操作：
- 选择数组 \(a\) 中的任意元素，并将其增加 1；
- 选择数组 \(a\) 中的任意元素，并将其减少 1；
- 从数组 \(a\) 中任意选择一个元素，复制并追加到数组 \(a\) 的末尾。
你的任务是计算将数组 \(a\) 转换为数组 \(b\) 所需的上述操作的最少次数（可能为零）。可以证明，在问题的限制条件下，这总是可能的。
输入
第一行包含一个整数 \(t\) \((1 \leq t \leq 10^4)\) — 测试用例的数量。
每个测试用例由三行组成：
- 第一行包含一个整数 \(n\) \((1 \leq n \leq 2 \times 10^5)\)；
- 第二行包含 \(n\) 个整数 \(a_1, a_2, \dots, a_n\) \((1 \leq a_i \leq 10^9)\)；
- 第三行包含 \(n+1\) 个整数 \(b_1, b_2, \dots, b_{n+1}\) \((1 \leq b_i \leq 10^9)\)。
输入的附加限制：所有测试用例中 \(n\) 的总和不超过 \(2 \times 10^5\)。
输出
对于每个测试用例，打印一个整数 — 将数组 \(a\) 转换为数组 \(b\) 所需的最少操作数（可能为零）。
示例
输入
3
1
2
1 3
2
3 3
3 3 3
4
4 2 1 2
2 1 5 2 3
输出
3
1
8
注
在第一个示例中，可以将 \(a\) 转换为 \(b\) 如下：\([2] \rightarrow [2,2] \rightarrow [1,2] \rightarrow [1,3]\)。
解题思路
对于\(a_i->bi,1\le i \le n\)，转变的最小代价就是它们的差值。
对于\(b_{n+1}\)，得到它的最小代价就是\(a_i->b_i\)过程中与它最小的差值\(+1\)。
题解
void solve()
{
int n;
cin >> n;
vi a(n);
for (int i = 0; i < n; i++)
{
cin >> a[i];
}
vi b(n + 1);
for (int i = 0; i < n + 1; i++)
{
cin >> b[i];
}
int need = INF;
ll ans = 0;
for (int i = 0; i < n; i++)
{
ans += abs(b[i] - a[i]);
need = min(need, abs(b[n] - b[i]));
need = min(need, abs(b[n] - a[i]));
if (a[i] < b[n] && b[n] < b[i] || a[i] > b[n] && b[n] > b[i])
need = 0;
}
cout << ans + need + 1 << endl;
}
int main()
{
ios::sync_with_stdio(false), std::cin.tie(nullptr), std::cout.tie(nullptr);
int _ = 1;
std::cin >> _;
while (_--)
{
solve();
}
return 0;
}
Problem - 1976C - Codeforces
C. 工作面试
Monocarp 打算开一家自己的 IT 公司。他想招聘 \(n\) 名程序员和 \(m\) 名测试员。
有 \(n + m + 1\) 个候选人，按到达时间顺序从 1 到 \(n + m + 1\) 依次编号。第 \(i\) 名候选人的编程技能为 \(a_i\)，测试技能为 \(b_i\)（一个人的编程技能和测试技能是不同的）。团队的技能是所有被聘为程序员的候选人的编程技能之和，以及所有被聘为测试员的候选人的测试技能之和。
当应聘者前来面试时，Monocarp 会尝试将其分配到最适合的职位（如果应聘者的编程技能较高，则录用其为程序员，否则录用其为测试员）。如果该职位的所有名额都已招满，Monocarp 就会将他们分配到其他职位。
你的任务是，针对每个候选人，计算如果除他们之外的所有人都来面试，团队的技能。请注意，这意味着正好有 \(n + m\) 名候选人来参加面试，因此公司的所有 \(n + m\) 个职位都将被填满。
输入
第一行包含一个整数 \(t\) \((1 \leq t \leq 10^4)\) — 测试用例的数量。
每个测试用例由三行组成：
- 第一行包含两个整数 \(n\) 和 \(m\) \((0 \leq n, m \leq 2 \cdot 10^5; 2 \leq n + m + 1 \leq 2 \cdot 10^5)\) — 分别是 Monocarp 希望雇用的程序员人数和测试员人数；
- 第二行包含 \(n + m + 1\) 个整数 \(a_1, a_2, \dots, a_{n+m+1}\) \((1 \leq a_i \leq 10^9)\)，其中 \(a_i\) 是第 \(i\) 个候选人的编程技能；
- 第三行包含 \(n + m + 1\) 个整数 \(b_1, b_2, \dots, b_{n+m+1}\) \((1 \leq b_i \leq 10^9; b_i \neq a_i)\)，其中 \(b_i\) 是第 \(i\) 个候选人的测试技能。
输入的附加限制：所有测试用例的 \((n + m + 1)\) 之和不超过 \(2 \cdot 10^5\)。
输出
对于每个测试用例，打印 \(n + m + 1\) 个整数，其中第 \(i\) 个整数应该等于如果除了第 \(i\) 个候选人之外的所有人都来面试时团队的技能。
示例
输入
4
1 0
2 1
1 2
0 2
4 5 5
5 4 1
1 2
2 1 5 4
5 2 3 1
3 1
4 3 3 4 1
5 5 4 5 2
输出
1 2
5 6 9
8 11 11 12
13 13 13 12 15
说明
让我们来看看示例中的第三个测试案例：
- 如果第一个候选者没有来，第二个候选者会被聘为测试员，第三个候选者会被聘为程序员，第四个候选者会被聘为测试员。团队的总技能为 \(2 + 5 + 1 = 8\)；
- 如果第二个候选者没有来，第一个候选者会被聘为测试员，第三个候选者会被聘为程序员，第四个候选者会被聘为测试员。团队的总技能为 \(5 + 5 + 1 = 11\)；
- 如果第三个候选者没有来，第一个候选者会被聘为测试员，第二个候选者会被聘为测试员，第四个候选者会被聘为程序员。团队的总技能为 \(5 + 2 + 4 = 11\)；
- 如果第四个候选者没有来，第一个候选者会被聘为测试员，第二个候选者会被聘为测试员，第三个候选者会被聘为程序员。团队的总技能为 \(5 + 2 + 5 = 12\)。
解题思路
从前往后遍历，检查一下是\(a\)能力值浪费了还是\(b\)能力值浪费了，然后从后往前枚举，开一个数组维护一下最近后缀损失能力值。输出答案的时候，如果当前的人的站的职位刚好是能力值被浪费的职位，输出总和减去当前的人的能力值加上最近损失能力值
题解
typedef struct people
{
ll a;
ll b;
int job; // 被分配到了a职位就是1，b职位就是2
bool lose; // 是否浪费了能力
} people;
void solve()
{
int n, m;
cin >> n >> m;
int N = n + m + 1;
vector<people> p(N + 1);
for (int i = 1; i <= N; i++)
{
cin >> p[i].a;
}
for (int i = 1; i <= N; i++)
{
cin >> p[i].b;
}
// 能力总和
ll sum = 0;
// 哪种能力被浪费了
int sta = 0;
for (int i = 1; i <= N; i++)
{
if (p[i].a > p[i].b)
{
// a职位减1
n--;
// a职位没有了
if (n < 0)
{
sta = 1; // 有人的a能力被浪费了
sum += p[i].b;
p[i].job = 2; // 这个人被分配到了b职位
p[i].lose = true; // 他的能力被浪费了
}
else
{
sum += p[i].a;
p[i].job = 1; // 这个人被分配到了a职位
p[i].lose = false; // 他没有能力被浪费
}
}
else
{
// b职位减1
m--;
// b职位没有了
if (m < 0)
{
sta = 2; // 有人的b能力被浪费了
sum += p[i].a;
p[i].job = 1; // 这个人被分配到了a职位
p[i].lose = true; // 他的能力被浪费了
}
else
{
sum += p[i].b;
p[i].job = 2; // 这个人被分配到了b职位
p[i].lose = false; // 他没有能力被浪费
}
}
}
// 最近被浪费的能力值
vl nearest_loss(N + 1);
// 从后往前遍历
for (int i = N; i >= 1; i--)
{
// 如果这个人能力被浪费了，那么最近被浪费的能力值就是他能力值和另一个能力值之差的绝对值
if (p[i].lose)
nearest_loss[i] = abs(p[i].a - p[i].b);
// 如果这个人能力没有被浪费，那么最近被浪费的能力值就是下一个人的最近被浪费的能力值
else
nearest_loss[i] = nearest_loss[i + 1];
}
// 从前往后输出
for (int i = 1; i <= N; i++)
{
// 输出总和减去当前的人的能力值，判断一下他是否空出了位置给能力被浪费的人，是的话加上最近被浪费的能力值
cout << sum - (p[i].job == 1 ? p[i].a : p[i].b) + (p[i].job == sta ? nearest_loss[i] : 0) << " ";
}
cout << endl;
}
int main()
{
ios::sync_with_stdio(false), std::cin.tie(nullptr), std::cout.tie(nullptr);
int _ = 1;
std::cin >> _;
while (_--)
{
solve();
}
return 0;
}
Problem - 1976D - Codeforces
D. 可逆括号序列
一个正则括号序列是指可以通过在序列的原始字符之间插入字符 '1' 和 '+' 来转换成正确算术表达式的括号序列。例如：
- 括号序列 "()" 和 "(())" 是正则的（得到的表达式分别是："(1)+(1)" 和 "((1+1)+1)"）；
- 括号序列 ")(", "(" 和 ")" 不是正则的。
我们定义括号序列的逆序如下：用 ')' 替换所有括号 '('，反之亦然（用 '(' 替换所有括号 ')'）。例如，字符串 "()((" 和 ")())" 互为逆序。
给你一个正则括号序列 \(s\)。计算满足以下条件的整数对 \((l, r)\) 的数量（1 ≤ l ≤ r ≤ |s|）：如果将 \(s\) 中从第 \(l\) 个字符到第 \(r\) 个字符（包含第 \(l\) 和第 \(r\) 个字符）的子串替换成其逆序，\(s\) 仍然是一个正则括号序列。
输入
第一行包含一个整数 \(t\) \((1 \leq t \leq 10^4)\) — 测试用例的数量。
每个测试用例的唯一一行包含一个非空的正则括号序列；该序列仅由字符 '(' 和 ')' 组成。
输入的附加限制：所有测试用例的正则括号序列总长度不超过 \(2 \cdot 10^5\)。
输出
对于每个测试用例，打印一个整数 — 符合题目条件的 \((l, r)\) 对的数量。
示例
输入
4
(())
()
()()()
(()())(())
输出
1
0
3
13
说明
在第一个示例中，只有一对：
- \((2, 3)\): (()) → ()().
在第二个示例中，没有一对。
在第三个示例中，有三对：
- \((2, 3)\): ()()() → (())().
- \((4, 5)\): ()()() → ()(()).
- \((2, 5)\): ()()() → (()()).
解题思路
我们将"("转化成\(+1\)，将")"转化成\(-1\)。对字符串做前缀和，我们就得到了一个在数轴上的折线。
选择一个区间翻转，实际上就是将这条折线沿着线段\(l-r\)翻折。
下图是测试用例\(3\)的折线图和可翻转的点。
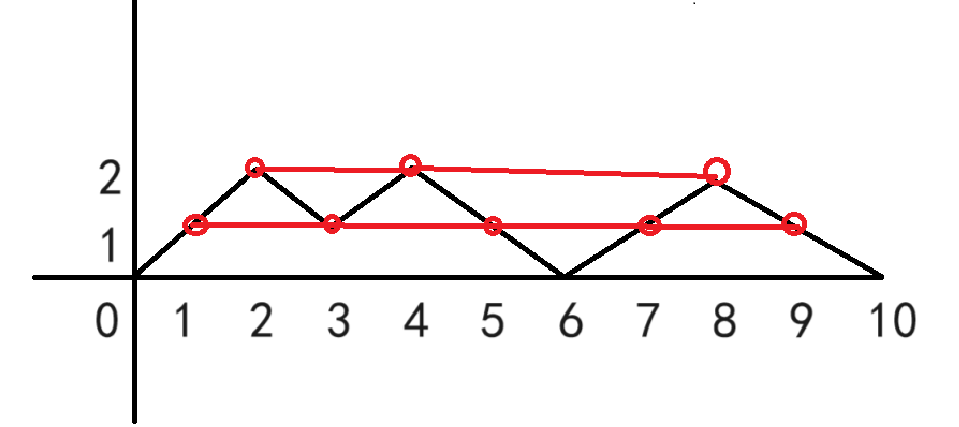
不难发现，满足题目要求的区间\([l,r]\)，一定满足\(sum[l]>=0，sum[r]==sum[l-1],max(sum[l\sim r])<=2 \times sum[r]\)
从前往后枚举\(sum\)统计一下高度相同的点的数量并累加即可。注：如果翻转会到达负值域的点要赋值为0。
题解
void solve()
{
string s;
cin >> s;
int n = s.size();
vi sum(n + 1);
for (int i = 0; i < n; i++)
{
sum[i + 1] = sum[i] + (s[i] == '(' ? 1 : -1);
}
vi high(n + 1);
high[0] = 1;
ll ans = 0;
for (int i = 1; i <= n; i++)
{
ans += high[sum[i]];
high[sum[i]]++;
if (sum[i] > 0)
high[(sum[i] - 1) / 2] = 0;
}
cout << ans << endl;
}
int main()
{
ios::sync_with_stdio(false), std::cin.tie(nullptr), std::cout.tie(nullptr);
int _ = 1;
std::cin >> _;
while (_--)
{
solve();
}
return 0;
}
