面试高频算法
常用算法如下:
1、冒泡排序
for(int i=0;i<n;i++){
for(int j=0;j<n-1-i;j++){
if(temp[j]>temp[j+1]){
int t=temp[j];
temp[j]=temp[j+1];
temp[j+1]=t;
}
}
}
2、快速排序
public void quicksort(int[] array,int left,int right){
if(left<right){
int key = array[left];
int low = left;
int high = right;
while(low<high){
while(low<high && array[high]>=key){
high--;
}
array[low] = array[high];
while(low<high && array[low]<=key){
low++;
}
array[high] = array[low];
}
array[low] = key;
quicksort(array,left,low-1);
quicksort(array,low+1,right);
}
}
3、二分查找
public class TestA {
public static <T extends Comparable<T>> int binarySearch(T[] x, T key) {
return binarySearch(x, 0, x.length - 1, key);
}
// 使用循环实现的二分查找
public static <T> int binarySearch(T[] x, T key, Comparator<T> comp) {
int low = 0;
int high = x.length - 1;
while (low <= high) {
int mid = (low + high) >>> 1;
int cmp = comp.compare(x[mid], key);
if (cmp < 0) {
low = mid + 1;
} else if (cmp > 0) {
high = mid - 1;
} else {
return mid;
}
}
return -1;
}
// 使用递归实现的二分查找
private static <T extends Comparable<T>> int binarySearch(T[] x, int low, int high, T key) {
if (low <= high) {
int mid = low + ((high - low) >> 1);
if (key.compareTo(x[mid]) == 0) {
return mid;
} else if (key.compareTo(x[mid]) < 0) {
return binarySearch(x, low, mid - 1, key);
} else {
return binarySearch(x, mid + 1, high, key);
}
}
return -1;
}
}
4、堆排序
public void HeapAdjust(int[] array, int parent, int length) {
int temp = array[parent]; // temp保存当前父节点
int child = 2 * parent + 1; // 先获得左孩子
while (child < length) {
// 如果有右孩子结点,并且右孩子结点的值大于左孩子结点,则选取右孩子结点
if (child + 1 < length && array[child] < array[child + 1]) {
child++;
}
// 如果父结点的值已经大于孩子结点的值,则直接结束
if (temp >= array[child])
break;
// 把孩子结点的值赋给父结点
array[parent] = array[child];
// 选取孩子结点的左孩子结点,继续向下筛选
parent = child;
child = 2 * child + 1;
}
array[parent] = temp;
}
public void heapSort(int[] list) {
// 循环建立初始堆
for (int i = list.length / 2-1; i >= 0; i--) {
HeapAdjust(list, i, list.length);
}
// 进行n-1次循环,完成排序
for (int i = list.length - 1; i > 0; i--) {
// 最后一个元素和第一元素进行交换
int temp = list[i];
list[i] = list[0];
list[0] = temp;
// 筛选 R[0] 结点,得到i-1个结点的堆
HeapAdjust(list, 0, i);
System.out.format("第 %d 趟: \t", list.length - i);
printPart(list, 0, list.length - 1);
}
}
5、查找子字符串出现的第一个索引位置
类似于Java的indexof()方法的实现,如下:
static int indexOf(char[] source, char[] target) {
char first = target[0];
int max = (source.length - target.length);
for (int i = 0; i <= max; i++) {
/* Look for first character. */
if (source[i] != first) {
while (++i <= max && source[i] != first)
;
}
/* Found first character, now look at the rest of v2 */
if (i <= max) {
int j = i + 1;
int end = j + target.length - 1;
for (int k = 1; j < end && source[j] == target[k]; j++, k++)
;
if (j == end) {
/* Found whole string. */
return i;
}
}
}
return -1;
}
6、分层打印二叉树并在每一层输出换行
public void PrintFromTopToBottom(TreeNode root) {
TreeNode currentNode = root;
int first = 1;
int second = 0;
while (currentNode != null) {
if (currentNode.left != null) {
queue.add(currentNode.left);
second++;
}
if (currentNode.right != null) {
queue.add(currentNode.right);
second++;
}
first--;
System.out.print(currentNode.val + " ");
if (first == 0) {
System.out.println(" ");
first = second;
second = 0;
}
currentNode = queue.poll();
}
}
Queue 中 remove() 和 poll()都是用来从队列头部删除一个元素。
Queue 中 add() 和 offer()都是用来向队列添加一个元素。在容量已满的情况下,add() 方法会抛出IllegalStateException异常,offer() 方法只会返回 false 。
7、一致性hash
一致性hash算法可以解决容错性和扩展性的问题。
系统中增加更多的虚拟节点,可以更好的解负载均衡问题。
public class Shard<S> { // S类封装了机器节点的信息 ,如name、password、ip、port等
private TreeMap<Long, S> circle; // 将整个hash值空间组成一个虚拟的环
private List<S> shards; // 真实机器节点
private final int NODE_NUM = 100; // 每个机器节点关联的虚拟节点个数
private final HashFunction hashFunction; // 选择一个碰撞率低的hash()函数
public Shard(List<S> shards,HashFunction hashFunction) {
super();
this.shards = shards;
this.hashFunction = hashFunction;
init();
}
private void init() { // 初始化一致性hash环
circle = new TreeMap<Long, S>();
for (int i = 0; i<shards.size(); ++i) { // 每个真实机器节点都需要关联虚拟节点
final S shardInfo = shards.get(i);
add(shardInfo);
}
}
public void add(S node) {
for (int i = 0; i < NODE_NUM; i++) {
// 虚拟节点用一些特定的hash值来替代,这样形成了hash值到真实节点的映射
circle.put(hashFunction.hash(node.toString() + i), node);
}
}
public void remove(S node) {
for (int i = 0; i < NODE_NUM; i++) {
// 移除真实节点下对应的所有虚拟节点(特定的一些hash值)
circle.remove(hashFunction.hash(node.toString() + i));
}
}
public S getShardInfo(String key) {
if (circle.isEmpty()) {
return null;
}
Long hash = hashFunction.hash(key);
// 如果当前hash值没有定位到虚拟节点,tailMap(T fromKey) 方法返回一个包含了不小于给定 fromKey 的 key 的子 map
if (!circle.containsKey(hash)) {
SortedMap<Long, S> tailMap = circle.tailMap(hash);
hash = tailMap.isEmpty() ? circle.firstKey() : tailMap.firstKey();
}
return circle.get(hash);
}
}
机器节点的定义如下:
class Machine {
String ip;
String name;
public Machine(String ip, String name) {
this.ip = ip;
this.name = name;
}
public String getIp() {
return ip;
}
public void setIp(String ip) {
this.ip = ip;
}
public String getName() {
return name;
}
public void setName(String name) {
this.name = name;
}
}
public class Test {
public static void main(String[] args) {
Machine a = new Machine("192.168.0.1", "a");
Machine b = new Machine("192.168.0.2", "b");
Machine c = new Machine("192.168.0.3", "c");
List<Machine> list = Arrays.asList(a, b, c);
Map<String, Integer> map = new HashMap<String, Integer>();
Shard<Machine> mcs = new Shard<Machine>(list, new HashFunction());
// 存储0到2000个数,看存储在各个机器上的数的数量是否大致均匀
for (int i = 0; i < 2000; i++) {
String key = i + "";
Machine m = mcs.getShardInfo(key);
if (map.get(m.getIp()) == null) {
map.put(m.getIp(), 0);
} else {
map.put(m.getIp(), (int) map.get(m.getIp()) + 1);
}
}
Iterator<Entry<String, Integer>> iterator = map.entrySet().iterator();
while (iterator.hasNext()) {
Entry<String, Integer> entry = iterator.next();
System.out.println(entry.getKey() + "/" + entry.getValue());
}
}
}
某次运行后的结果如下:
192.168.0.2/599
192.168.0.1/698
192.168.0.3/700
8、LRU最近最少使用算法
要效率的话使用hash搜索,要实现最近最少的话就用双向链表
public class LRUCache {
private int cacheSize;
private HashMap<Object, Entry> nodes; // 缓存容器 ,为了提高查询速度需要这个结构
private int currentSize;
private Entry first; // 链表头
private Entry last; // 链表尾
static class Entry {
Entry prev;
Entry next;
Object key;
Object value;
}
public LRUCache(int i) {
currentSize = 0;
cacheSize = i;
nodes = new HashMap<Object, Entry>(i);
}
/**
* 获取缓存中对象,并把它放在最前面
*/
public Entry get(Object key) {
Entry node = nodes.get(key);
if (node != null) {
moveToHead(node);
return node;
} else {
return null;
}
}
/**
* 添加 entry到hashtable, 并把entry
*/
public void put(Object key, Object value) {
//先查看hashtable是否存在该entry, 如果存在,则只更新其value
Entry node = nodes.get(key);
if (node == null) {
//缓存容器是否已经超过大小.
if (currentSize >= cacheSize) {
nodes.remove(last.key);
removeLast();
} else {
currentSize++;
}
node = new Entry();
}
node.value = value;
//将最新使用的节点放到链表头,表示最新使用的.
moveToHead(node);
nodes.put(key, node);
}
/**
* 将entry删除, 注意:删除操作只有在cache满了才会被执行
*/
public void remove(Object key) {
Entry node = nodes.get(key);
//在链表中删除
if (node != null) {
if (node.prev != null) {
node.prev.next = node.next;
}
if (node.next != null) {
node.next.prev = node.prev;
}
if (last == node)
last = node.prev;
if (first == node)
first = node.next;
}
//在hashtable中删除
nodes.remove(key);
}
/**
* 删除链表尾部节点,即使用最后 使用的entry
*/
private void removeLast() {
//链表尾不为空,则将链表尾指向null. 删除连表尾(删除最少使用的缓存对象)
if (last != null) {
if (last.prev != null){
last.prev.next = null;
}
else{
first = null;
}
last = last.prev;
}
}
/**
* 移动到链表头,表示这个节点是最新使用过的
*/
private void moveToHead(Entry node) {
if (node == first)
return;
if (node.prev != null)
node.prev.next = node.next;
if (node.next != null)
node.next.prev = node.prev;
if (last == node)
last = node.prev;
if (first != null) {
node.next = first;
first.prev = node;
}
first = node;
node.prev = null;
if (last == null){
last = first;
}
}
/*
* 清空缓存
*/
public void clear() {
first = null;
last = null;
currentSize = 0;
}
}
或者还有如下实现方式:
LinkedHashMap维护着一个运行于所有条目的双重链接列表。此链接列表定义了迭代顺序,该迭代顺序可以是插入顺序(insert-order)或者是访问顺序,其中默认的迭代访问顺序就是插入顺序,即可以按插入的顺序遍历元素。基于LinkedHashMap的访问顺序的特点,可构造一个LRU(Least Recently Used)最近最少使用简单缓存。也有一些开源的缓存产品如ehcache的淘汰策略(LRU)就是在LinkedHashMap上扩展的。
public class LruCache<K, V> extends LinkedHashMap<K, V> {
/** 最大容量 */
private int maxCapacity;
public LruCache(int maxCapacity) {
super(16, 0.75f, true);
this.maxCapacity = maxCapacity;
}
public int getMaxCapacity() {
return this.maxCapacity;
}
public void setMaxCapacity(int maxCapacity) {
this.maxCapacity = maxCapacity;
}
/**
* 当列表中的元素个数大于指定的最大容量时,返回true,并将最老的元素删除。
*/
@Override
protected boolean removeEldestEntry(java.util.Map.Entry<K, V> eldest) {
if (super.size() > maxCapacity) {
return true;
}
return false;
}
}
public class LruCacheTest {
public static void main(String[] args) {
LruCache<String, Object> cache = new LruCache<String, Object>(10);
for (int i = 1; i <= 15; i++) {
cache.put(i + "", i);
}
// 此时访问指定KEY的元素
cache.get("10");
Iterator<Entry<String, Object>> iterator = cache.entrySet().iterator();
for (; iterator.hasNext();) {
Entry<String, Object> entry = iterator.next();
System.out.println("key=" + entry.getKey() + ",value=" + entry.getValue());
}
}
}
输出如下:
key=7,value=7
key=8,value=8
key=9,value=9
key=11,value=11
key=12,value=12
key=13,value=13
key=14,value=14
key=15,value=15
key=10,value=10
9、生产者与消费者
package com.cpuhigh;
public class ConsumerProducerByWaitNotify {
public Integer monitor = new Integer(1);
public static void main(String[] args) {
ConsumerProducerByWaitNotify instance = new ConsumerProducerByWaitNotify();
instance.bootstrap();
}
public void bootstrap() {
Godown godown = new Godown(30); // 必须操作同一个库的实例,否则不存在多线程的问题
Consumer c1 = new Consumer(20, godown);
Consumer c2 = new Consumer(20, godown);
Producer p1 = new Producer(10, godown);
Producer p2 = new Producer(10, godown);
c1.start();
c2.start();
p1.start();
p2.start();
}
// 仓库
class Godown {
public static final int max_size = 100; // 最大库存量
public int curnum; // 当前库存量
Godown(int curnum) {
this.curnum = curnum;
}
// 生产指定数量的产品
public void produce(int neednum) {
synchronized (monitor) {
// 测试是否需要生产
while (neednum + curnum > max_size) {
System.out.println("要生产的产品数量" + neednum + "超过剩余库存量" + (max_size - curnum) + ",暂时不能执行生产任务!");
try {
// 当前的生产线程等待,并让出锁(注意,只有获取到锁,才有让锁的一说)
// 如果调用某个对象的wait()方法,当前线程必须拥有这个对象的monitor(即锁),
// 因此调用wait()方法必须在同步块或者同步方法中进行(synchronized块或者synchronized方法)
monitor.wait();
} catch (InterruptedException e) {
e.printStackTrace();
}
}
// 满足生产条件,则进行生产,这里简单的更改当前库存量
curnum += neednum;
System.out.println("已经生产了" + neednum + "个产品,现仓储量为" + curnum);
// 唤醒在此对象监视器上等待的所有线程
// 调用某个对象的notify()方法,当前线程也必须拥有这个对象的monitor,
// 因此调用notify()方法必须在同步块或者同步方法中进行(synchronized块或者synchronized方法)。
monitor.notifyAll();
}
}
// 消费指定数量的产品
public void consume(int neednum) {
synchronized (monitor) {
// 测试是否可消费
while (curnum < neednum) {
try {
// 当前的消费线程等待,并让出锁
monitor.wait();
} catch (InterruptedException e) {
e.printStackTrace();
}
}
// 满足消费条件,则进行消费,这里简单的更改当前库存量
curnum -= neednum;
System.out.println("已经消费了" + neednum + "个产品,现仓储量为" + curnum);
// 唤醒在此对象监视器上等待的所有线程
monitor.notifyAll();
}
}
}
// 生产者
class Producer extends Thread {
private int neednum; // 生产产品的数量
private Godown godown; // 仓库
Producer(int neednum, Godown godown) {
this.neednum = neednum;
this.godown = godown;
}
@Override
public void run() {
// 生产指定数量的产品
godown.produce(neednum);
}
}
// 消费者
class Consumer extends Thread {
private int neednum; // 生产产品的数量
private Godown godown; // 仓库
Consumer(int neednum, Godown godown) {
this.neednum = neednum;
this.godown = godown;
}
@Override
public void run() {
// 消费指定数量的产品
godown.consume(neednum);
}
}
}
还可以使用阻塞队列、Semaphore等手段来实现。
10、布隆过滤器
就是判断一个元素是否在一个集合中
布隆过滤器(Bloom Filter)的核心实现是一个超大的位数组和几个哈希函数。假设位数组的长度为m,哈希函数的个数为k
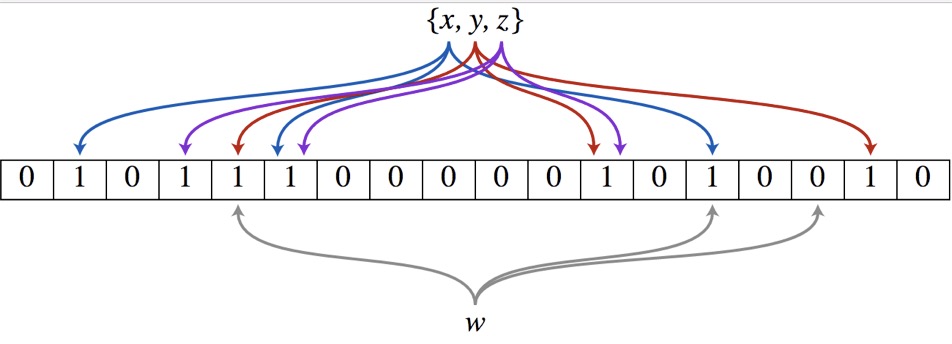
以上图为例,具体的操作流程:假设集合里面有3个元素{x, y, z},哈希函数的个数为3。首先将位数组进行初始化,将里面每个位都设置位0。对于集合里面的每一个元素,将元素依次通过3个哈希函数进行映射,每次映射都会产生一个哈希值,这个值对应位数组上面的一个点,然后将位数组对应的位置标记为1。查询W元素是否存在集合中的时候,同样的方法将W通过哈希映射到位数组上的3个点。如果3个点的其中有一个点不为1,则可以判断该元素一定不存在集合中。反之,如果3个点都为1,则该元素可能存在集合中。注意:此处不能判断该元素是否一定存在集合中,可能存在一定的误判率。可以从图中可以看到:假设某个元素通过映射对应下标为4,5,6这3个点。虽然这3个点都为1,但是很明显这3个点是不同元素经过哈希得到的位置,因此这种情况说明元素虽然不在集合中,也可能对应的都是1,这是误判率存在的原因。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号