Matlab——图形绘制——二维平面图形

二维平面图形

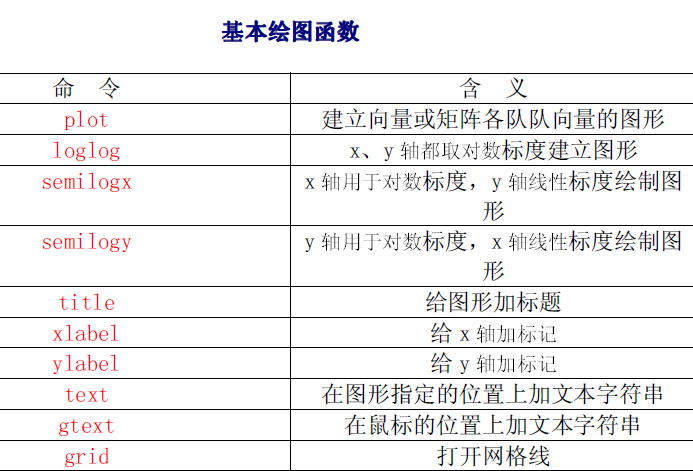
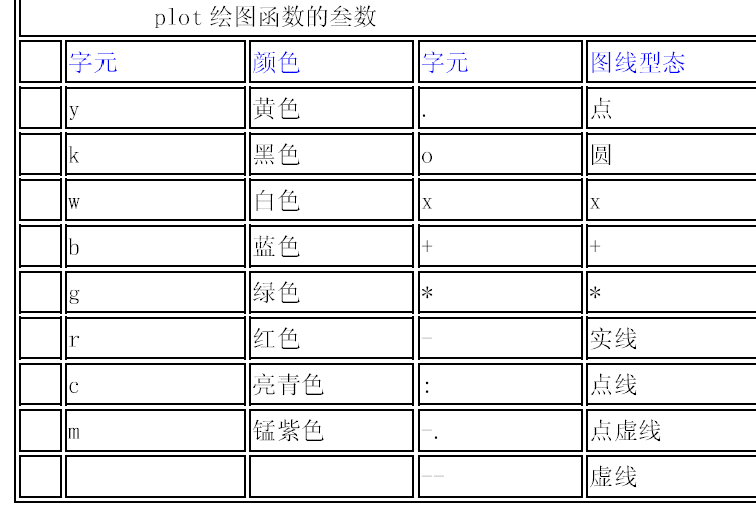
hold on ————在已画好的图形上添加新的图形

 

plot 是绘制一维曲线的基本函数，但在使用此函数之前，我们需先定义曲线上
每一点的x 及y 座标。下例可画出一条正弦曲线：

>> x=0:0.001:10; % 0 到10 的1000 个点的x 座标
y=sin(x); % 对应的y 座标
plot(x,y); % 绘图

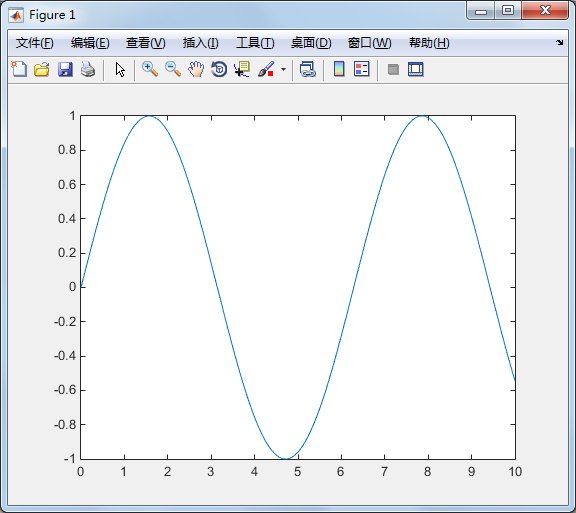
改变颜色

 

>> plot(x,y,'k')

 

 

 

改变颜色的同时改变图线形态

 

>> plot(x,y,'k*')

 

 

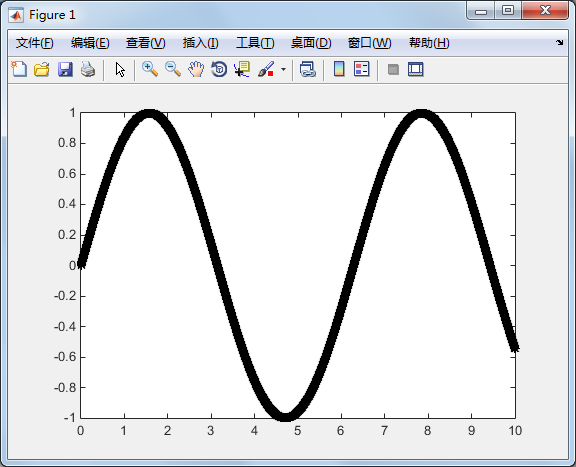
 同时画两个函数【淡粉色】

>> Y=sin(10*x);
plot(x,y,'r:',x,Y,'b') % 同时画两个函数

 

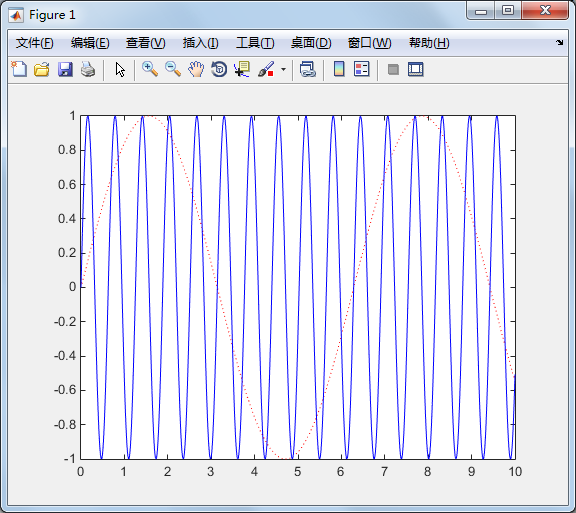
 调整图轴范围

>> axis([0,6,-1,1])   %前两个是横坐标，后两个是纵坐标

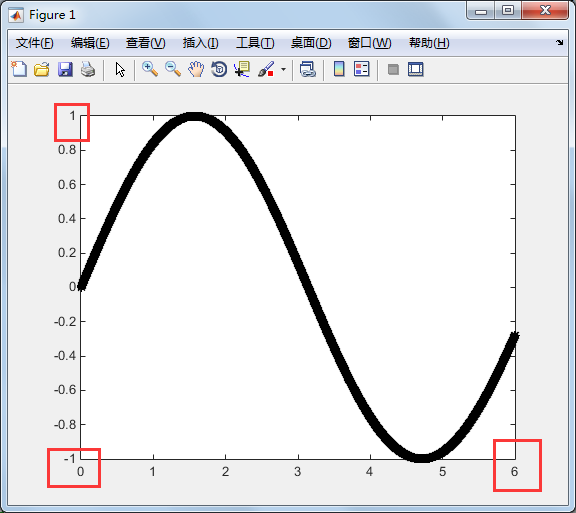
图形上加上注解

>> xlabel('x 轴'); % x 轴注解
ylabel('y 轴'); % y 轴注解
title('余弦函数'); % 图形标题
legend('y = cos(x)'); % 图形注解
gtext('y = cos(x)'); % 图形注解 ,用鼠标定位注解位置
grid on; % 显示格线

 

 

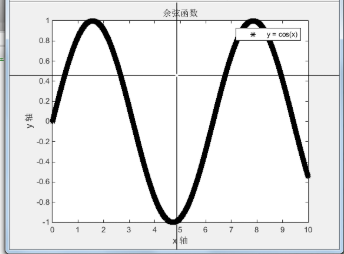
实例：将一函数 f(x)=sin(x)/x 在-20<x<20,-0.4<y<1.2 之间画出：

>> fplot('sin(x)./x',[-20 20 -0.4 1.2])

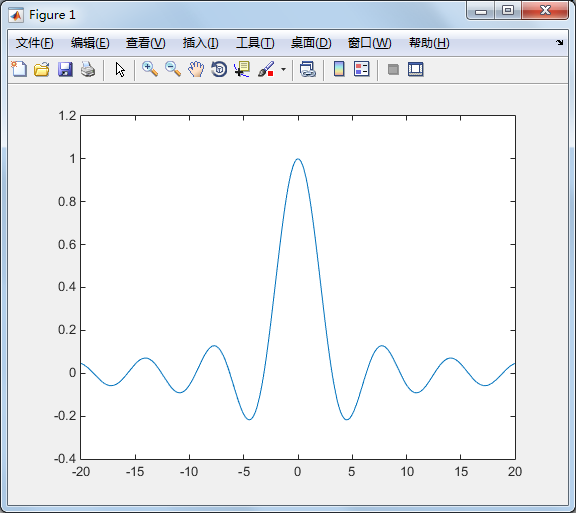
实例：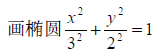

a = [0:pi/50:2*pi]'; %角度 0 − 2p
X = cos(a)*3; %参数方程
Y = sin(a)*2;
plot(X,Y);
xlabel('x'), ylabel('y');
title('椭圆')

 

图形窗口的分割一般用命令subplot:

>> subplot(2,2,1);
>> subplot(2,3,4);

 

当资料点数量不多时——长条图

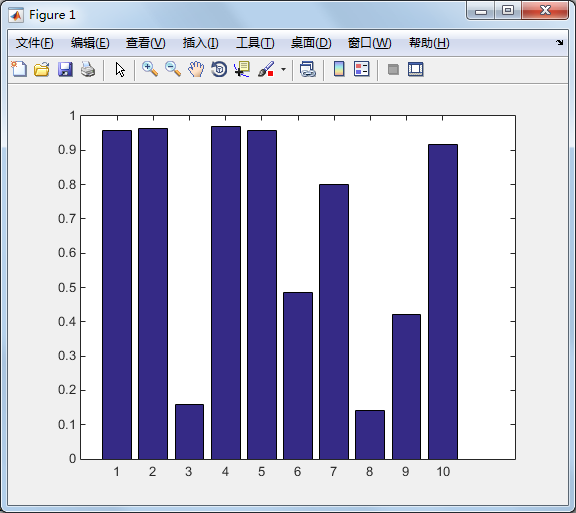
close all; %关闭所有的图形视窗
x=1:10;
y=rand(size(x));
bar(x,y);

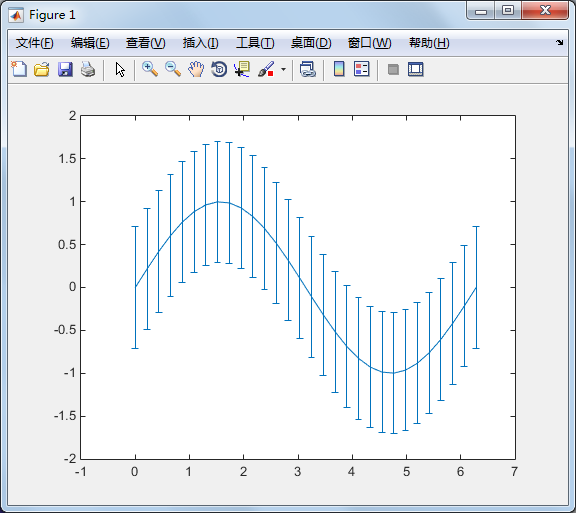
如果已知资料的误差量，就可用errorbar 来表示。下例以单位标准差来做资料
的误差量：

x = linspace(0,2*pi,30);
y = sin(x);
e = std(y)*ones(size(x));
errorbar(x,y,e)

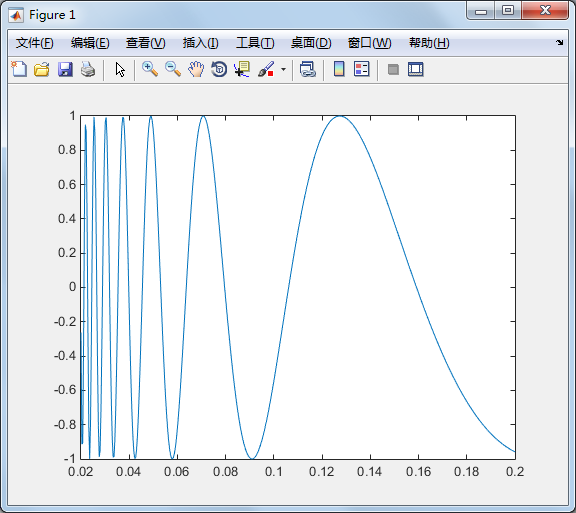
对於变化剧烈的函数，可用fplot 来进行较精确的绘图，会对剧烈变化处进行较
密集的取样，如下例：

>> fplot('sin(1/x)', [0.02 0.2]); % [0.02 0.2]是绘图范围

 

若要产生极座标图形，可用polar：

theta=linspace(0, 2*pi);
r=cos(4*theta);
polar(theta, r);

 

对於大量的资料，我们可用hist 来显示资料的分 情况和统计特性。下面几个
命令可用来验证randn 产生的高斯乱数分 ：

>> x=randn(5000, 1); %产生5000个μ=0，s=1的高斯乱数
>> hist(x,20) %20代表长条的个数

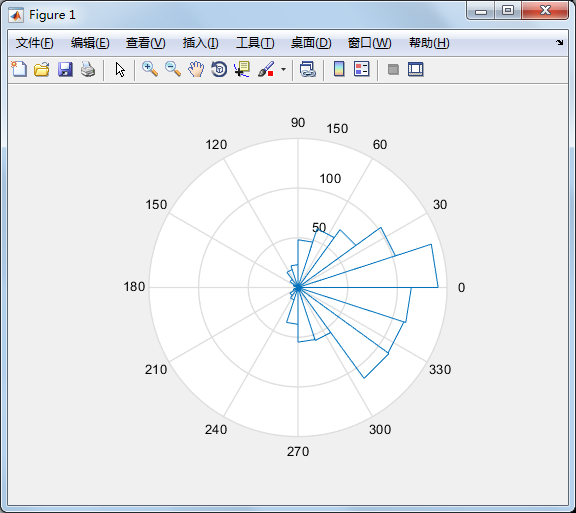
rose 和hist 很接近，只不过是将资料大小视为角度，资料个数视为距离，并用
极座标绘制表示：

x=randn(1000, 1);
rose(x);

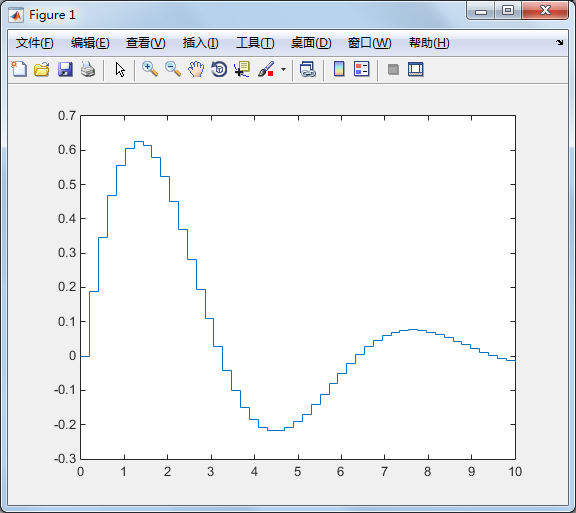
stairs 可画出阶梯图：

x=linspace(0,10,50);
y=sin(x).*exp(-x/3);
stairs(x,y);

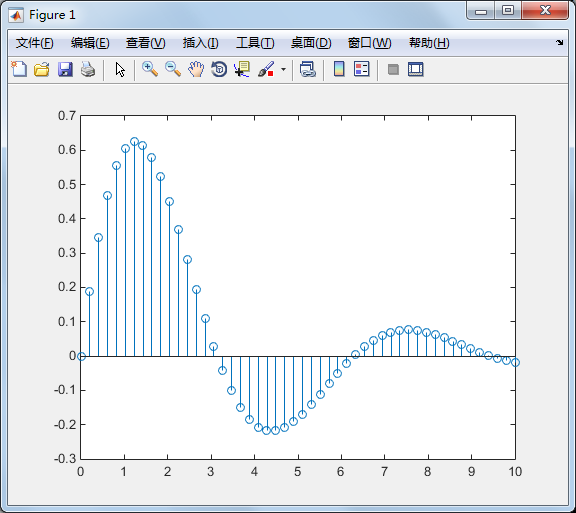
stems 可产生针状图，常被用来绘制数位讯号：

x=linspace(0,10,50);
y=sin(x).*exp(-x/3);
stem(x,y);

stairs 将资料点视为多边行顶点，并将此多边行涂上颜色：

>> x=linspace(0,10,50);
y=sin(x).*exp(-x/3);
fill(x,y,'b'); % 'b'为蓝色

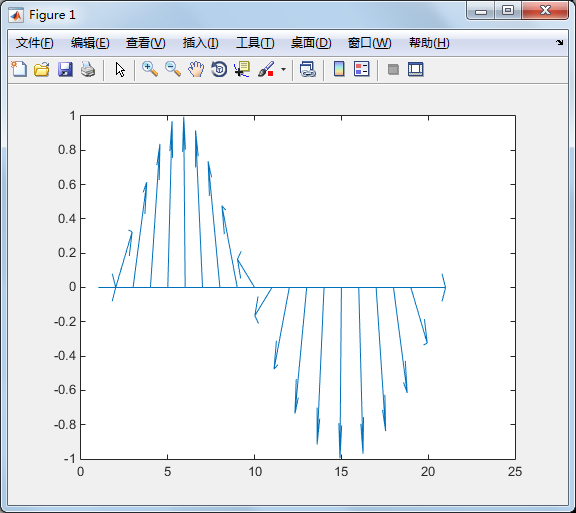
feather 将每一个资料点视复数，并以箭号画出：

theta=linspace(0, 2*pi, 20);
z = cos(theta)+i*sin(theta);
feather(z);

compass 和feather 很接近，只是每个箭号的起点都在圆点：

theta=linspace(0, 2*pi, 20);
z = cos(theta)+i*sin(theta);
compass(z);