机器学习【十二】使用管道模型对股票涨幅进行回归分析

书上数据集无法获得，所以，拍照之......

整理数据集：

• 删除无效数值
• 去掉冗余信息
• 考虑是否把字符串类型的特征通过get_dummies转化成整型数值

#导入pandas
import pandas as pd
stocks = pd.read_csv('文件路径',encoding='gbk')
#定义数据集中的特征X和目标y
X = stocks.loc[:,'现价'：'流通股（亿）'].values
y = stocks['涨幅%%']
#验证数据集形态
print(X.shape,y.shape)

（3421，23）（3421，）

【结果分析】

数据集加载成功，共有3421支股票，每支股票包含23个特征

 

尝试用MLP多层感知神经网络回归分析，评分仍然用交叉验证cross_val_score:

#导入交叉验证
from sklearn.model_selection import cross_val_score
#导入MLP神经网络
from sklearn.neural_network import MLPRegressor
#使用交叉验证对MLP模型评分
print('平均分：',lscores.mean())

-34870039.57

【结果分析】

原因在于，MLP对数据预处理的要求很高，而原始数据集中各个特征的数量级差的又远，必然很差

 

1.建立包含数据预处理和MLP模型的管道模型：

建立管道模型将数据预处理和MLP模型打包进去：

在sklearn中可以使用make_pipeline便捷的建立管道模型

#导入make_pipeline模块
from sklearn.pipeline import make_pipeline
#对比两种方式的语法
pipeline = Pipeline([('scaler',StandardScaler()),('mlp',MLPRegressor(random_state=38))])
pipe = make_pipeline(StandardScaler(),MLPRegressor(random_state=38)) #更简洁，不需要指定每个步骤的名称
#打印两种建立管道模型方法的步骤
print('*'*10)
print(pipeline.steps)
print('x'*10)
print(pipe.steps)

【结果分析】

 步骤如上，参数上看，两种方法得到的结果完全一致

 

尝试用交叉验证cross_val_score评分：

#进行交叉验证
scores = cross_val_score(pipe,X,y,cv=3)
print('模型平均分：',scores.mean())

0.90

 

 

2.向管道模型添加特征选择步骤

#导入特征选择模块
from sklearn.feature_selection import SelectFromModel
#导入随机森林模型
from sklearn.ensemble import RandomForestRegressor
#建立管道模型
pipe = make_pipeline(StandardScaler(),SelectFromModel(RandomForestRegressor(random_state=38)),MLPRegressor(random_state=38))
#显示管道模型步骤
pipe.steps

为了让多次运行的结果能够保持一致，也将随机森林的random_state进行指定

 

 

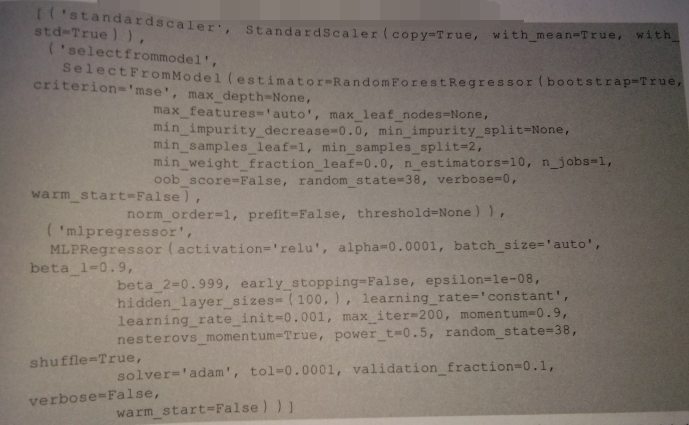
下面使用交叉验证法来给管道模型评分：

#使用交叉验证进行评分
scores = cross_val_score(pipe,X,y,cv=3)
print('管道模型平均分：',scores.mean())

0.89

【结果分析】

 对比没有添加模型选择的管道模型，得分有了提升

针对不同数据集，可以在管道模型中增加更多的步骤，以提高模型的性能表现 

 

提取管道模型每个步骤的属性，例如SelectFromModel 步骤中，模型选择了哪些特征：

#使用管道模型拟合数据
pipe.fit(X,y)
mask = pipe.named_steps['selectfrommodel'].get_support()
#打印特征选择的结果
print(mask)

 

 

 

3.使用管道模型进行模型选择和参数调优

 A.模型选择——从若干算法中找到适合我们数据集的算法

#定义参数字典
params = [{'reg':[MLPRegressor(random_state=38)],'scaler':[StandardScaler(),None]},{'reg':[RandomForestRegressor(random_state=38)],'scaler':[None]}]
#下面对pipeline实例化
pipe = Pipeline([('scaler',StandardScaler()),('reg',MLPRegressor())])
#对管道模型进行网格搜索
grid = GridSearchCV(pipe,params,cv=3)
#拟合数据
grid.fit(X,y)
print('最佳模型：',grid.best_params_)
print('模型最佳得分：',grid.best_score_)

我们定义了一个字典的列表params作为pipeline的参数

在参数中，我们指定对MLP模型使用StandardScaler ,而RandomForest 不使用StandardScaler,所以scaler对应None

结果：

 

 

B.使用管道模型寻找更优参数

 在上一个例子中，我们对比的两个模型使用的基本都是默认参数，如MLP的隐藏层使用的是缺省值（100，），而随机森林使用的n_estimators也是默认10个

 

如果修改了参数，会不会MLP表现不如随机森林？

通过在网格搜索中扩大搜索空间，将需要对比的模型参数，也放进管道模型中进行对比：

#在参数字典中加入MLP隐藏层和随机森林中estimator数量的选项
params = [{'reg':[MLPRegressor(random_state=38)],'scaler':[StandardScaler(),None],'reg_hidden_layer_sizes':[(50,),(100,),(100,100)]},{'reg':[RandomForestRegressor(random_state=38)],'scaler':[None],'reg__n_estimators':[10,50,100]}]
#下面对pipeline实例化
pipe = Pipeline([('scaler',StandardScaler()),('reg',MLPRegressor())])
#对管道模型进行网格搜索
grid = GridSearchCV(pipe,params,cv=3)
#拟合数据
grid.fit(X,y)
print('最佳模型：',grid.best_params_)
print('模型最佳得分：',grid.best_score_)

让GridSearchCV遍历两个模型所给出的参数，结果：

【结果分析】

 两个模型的表现发生了逆转

 

如果多提供一些参数供管道模型进行选择，如让随机森林n_estimators数量可以选择500 或 1000，结果可能还会反转：

#再次给入新的参数字典
params = [{'reg':[MLPRegressor(random_state=38,max_iter=1000)],'scaler':[StandardScaler(),None],'reg_hidden_layer_sizes':[(50,),(100,),(100,100)]},{'reg':[RandomForestRegressor(random_state=38)],'scaler':[None],'reg__n_estimators':[100,500,1000]}]
#下面对pipeline实例化
pipe = Pipeline([('scaler',StandardScaler()),('reg',MLPRegressor())])
#对管道模型进行网格搜索
grid = GridSearchCV(pipe,params,cv=3)
#拟合数据
grid.fit(X,y)
print('最佳模型：',grid.best_params_)
print('模型最佳得分：',grid.best_score_)

【结果分析】

 没有出现所期待的剧情反转，增加了n_estimators数量的随机森林仍然没能超越MLP

说明，对于这个数据集来说，MLP更适合些