Tensorflow 安装 和 初识

Windows中 Anaconda，Tensorflow 和 Pycharm的安装和配置   https://blog.csdn.net/zhuiqiuzhuoyue583/article/details/84945596  

安装Tensorflow时，上方文章可能会出问题,用pip3 ………或 pip …Install --user …… https://blog.csdn.net/a781751136/article/details/80231406

一、初识Tensorflow

三好学生问题

三好学生的评分公式： 总分 = 德育分 * 0.6 + 智育 * 0.3 + 体育 * 0.1

计算 总分的公式实际上就是 把 3项分数 各自乘以 一个权重，再相加求和

 

要解决的问题：

有两个家长 知道自己孩子的总分和各个的成绩，想知道学校究竟是怎么算的？【也就是各个项的权重】

但是，这两位学生的成绩组成的公式中共有3个未知数，但此处只有两个式子，也就无法用解方程的方法获得答案

所以————> 神经网络~

 

（1）分析问题，搭建神经网络

 

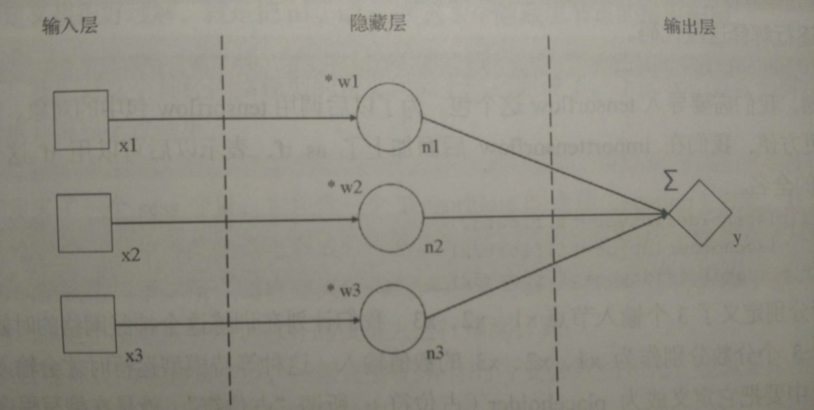
•  x1,x2,x3,n1,n2,n3,y —— 节点名称
• *w1，*w2,*w3,Σ  —— 节点运算

来模拟： 总分y = x1*w1 + x2*w2 + x3*w3;

 

代码如下：

import tensorflow as tf
x1 = tf.placeholder(dtype=tf.float32) 
#placeholder 占位符 —— 等待模型运行时 才会输入的节点，要定义成“占位符”
#dtype=tf.float32  —— 数据类型是 32位浮点小数
x2 = tf.placeholder(dtype=tf.float32)
x3 = tf.placeholder(dtype=tf.float32)
#意思是 —— 定义一个占位符变量x3 ，其数据类型是 32位浮点小数


#类似权重这种 在训练过程中经常变换的神经元参数，tensorflow称之为“变量”，此处为防止混淆，用“神经元的可变参数”
#并指定 可变参数初始值为 0.1
w1 = tf.Variable(0.1,dtype=tf.float32)
w2 = tf.Variable(0.1,dtype=tf.float32)
w3 = tf.Variable(0.1,dtype=tf.float32)

n1 = x1 * w1
n2 = x2 * w2
n3 = x3 * w3
y = n1 + n2 + n3

#sess变量，包含了tensorflow 的session会话对象【这玩意是啥，后期说】，现在可以简单的理解成 —— 管理神经网络运行的一个对象
sess = tf.Session()
#会话对象管理神经网络第一步 —— 一般是要把所有的可变参数 初始化
#tf.global_variables_initializer() 返回一个专门用于初始化可变参数的对象，调用 sess会话对象的成员函数 run() 
init = tf.global_variables_initializer()
sess.run(init)

#执行一次神经网络的计算
#第一个参数是一个数组，代表我们需要查看哪些结果项
#另一个参数是个 命名参数，代表我们要输入的数据 ———— 输入的是字典类型的值，必须用 {} 括起来，里面分别按 占位符的名称 一个个指明数值
result = sess.run([x1,x2,x3,w1,w2,w3,y],feed_dict={x1:90,x2:80,x3:70})
print(result)

[array(90., dtype=float32), array(80., dtype=float32), array(70., dtype=float32), 0.1, 0.1, 0.1, 24.0]

可以在上方的输出结果中发现：输入的分数 + 可变参数 + 最后总结果y

验证下，y = 90*0.1+80*0.1+70*0.1 = 24

 

 

 

(2)训练神经网络

神经网络的训练过程：

1. 输入数据 
2. 计算结果 —— 神经网根据 输入的数据和当前的可变参数值计算结果
3. 计算误差 —— 将计算的结果和标准答案对比，得出误差
4. 调整神经网络的可变参数 —— 根据误差的大小，使用反向传播算法，对神经网络中的可变参数调节
5. 再次训练 

import tensorflow as tf

x1 = tf.placeholder(dtype=tf.float32) 
x2 = tf.placeholder(dtype=tf.float32)
x3 = tf.placeholder(dtype=tf.float32)
#期待的对应结果值 —— “目标值”
yTrain = tf.placeholder(dtype=tf.float32)

w1 = tf.Variable(0.1,dtype=tf.float32)
w2 = tf.Variable(0.1,dtype=tf.float32)
w3 = tf.Variable(0.1,dtype=tf.float32)

n1 = x1 * w1
n2 = x2 * w2
n3 = x3 * w3
y = n1 + n2 + n3
#tf.abs() 函数用来计算绝对值 —— 计算误差
loss = tf.abs(y - yTrain)
#优化器变量optimizer —— 优化器就是用来调整神经网络可变参数的对象
optimizer = tf.train.RMSPropOptimizer(0.001) #选取了一种优化器，参数0.001是这个优化器的学习率
#学习率决定了优化器每次调整参数的幅度大小

#训练对象 train,train代表了我们准备如何来训练这个神经网络
train = optimizer.minimize(loss)  #这里要求 把loss最小化的原则调整可变参数

sess = tf.Session()
init = tf.global_variables_initializer()
sess.run(init)
result = sess.run([train,x1,x2,x3,w1,w2,w3,y,yTrain,loss],feed_dict={x1:90,x2:80,x3:70,yTrain:85})
print(result)
# yTrain 是对应每一组输入数据的目标结果值
# 要求输出的结果数组中多加了一个 train 对象，在结果数组中有train 对象，意味着要求程序执行一次train对象所包含的训练过程
# 在这个过程中，y,loss也会被计算出来，所以添加到结果数组中，方便对照
result = sess.run([train,x1,x2,x3,w1,w2,w3,y,yTrain,loss],feed_dict={x1:98,x2:95,x3:87,yTrain:96})
print(result)

[None, array(90., dtype=float32), array(80., dtype=float32), array(70., dtype=float32), 0.10316052, 0.10316006, 0.103159375, 24.0, array(85., dtype=float32), 61.0]
[None, array(98., dtype=float32), array(95., dtype=float32), array(87., dtype=float32), 0.10554425, 0.10563005, 0.1056722, 28.884804, array(96., dtype=float32), 67.1152]

只有在结果数组中加上了 训练对象，这次 sess.run() 函数的执行才算是 ”训练“，否则只是”运行“神经网络进行一次计算

 

我们可以看到，由于引入了训练过程，3个可变参数发生了变化

import tensorflow as tf

x1 = tf.placeholder(dtype=tf.float32) 
x2 = tf.placeholder(dtype=tf.float32)
x3 = tf.placeholder(dtype=tf.float32)
yTrain = tf.placeholder(dtype=tf.float32)
w1 = tf.Variable(0.1,dtype=tf.float32)
w2 = tf.Variable(0.1,dtype=tf.float32)
w3 = tf.Variable(0.1,dtype=tf.float32)
n1 = x1 * w1
n2 = x2 * w2
n3 = x3 * w3
y = n1 + n2 + n3
loss = tf.abs(y - yTrain)
optimizer = tf.train.RMSPropOptimizer(0.001) 
train = optimizer.minimize(loss)  
sess = tf.Session()
init = tf.global_variables_initializer()
sess.run(init)
for i in range(2):
    result = sess.run([train,x1,x2,x3,w1,w2,w3,y,yTrain,loss],feed_dict={x1:90,x2:80,x3:70,yTrain:85})
    print(result)
    result = sess.run([train,x1,x2,x3,w1,w2,w3,y,yTrain,loss],feed_dict={x1:98,x2:95,x3:87,yTrain:96})
    print(result)

[None, array(90., dtype=float32), array(80., dtype=float32), array(70., dtype=float32), 0.10316052, 0.10316006, 0.103159375, 24.0, array(85., dtype=float32), 61.0]
[None, array(98., dtype=float32), array(95., dtype=float32), array(87., dtype=float32), 0.10554425, 0.10563005, 0.1056722, 28.884804, array(96., dtype=float32), 67.1152]
[None, array(90., dtype=float32), array(80., dtype=float32), array(70., dtype=float32), 0.10740828, 0.107431844, 0.107439496, 25.346441, array(85., dtype=float32), 59.653557]
[None, array(98., dtype=float32), array(95., dtype=float32), array(87., dtype=float32), 0.10918032, 0.10926805, 0.10930761, 30.079273, array(96., dtype=float32), 65.92073]

总共进行了2轮训练，每轮两次

可以对比第一轮第一次和第二轮第一次的loss值，发现误差已经降低了

同理，第一轮第二次和第二轮第二次的loss值，误差也降低了

 

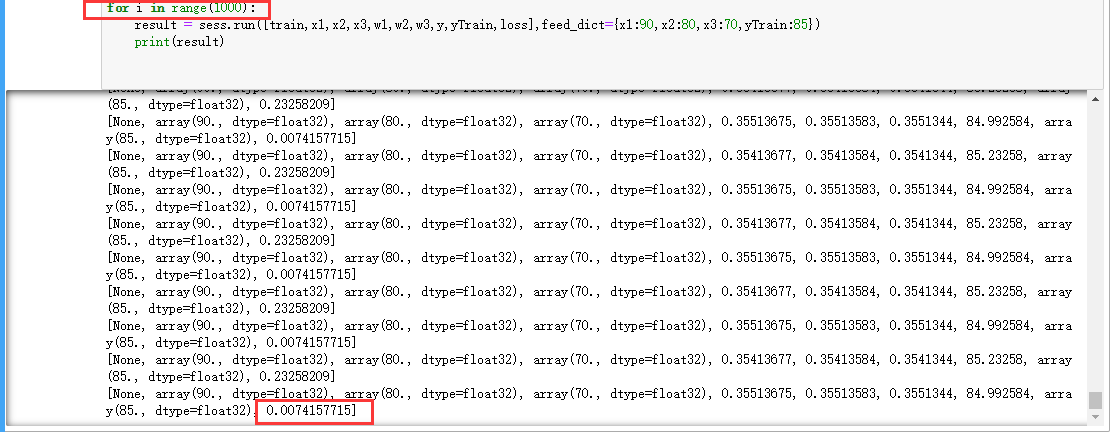
增大训练轮数，会发现两者的误差值会越来越小