[NOI2013]矩阵游戏
题意：
给定一次函数递推式，求第n项。n <= 1e(1e6)
解:
这么多位...
我们手动代入前几项，就能发现:
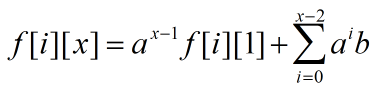
这个的左边可以用欧拉定理降幂，右边是个等比数列。
然后我们就可以求出f[i][1]和f[i + 1][1]之间的一次递推式了。
同理求出f[1][1]和f[n][1]之间的关系，然后就OK了。
以下这些点需要注意：
公比可能为1
随时取模！我就是在给等比数列求和函数传参的时候没有对首项取模导致只有15分...
第二次使用上面那个式子的时候注意所有的a和b都要随之变化！
用字符串读入nm，计算的时候逐位加起来同时取模。
1 #include <cstdio> 2 #include <cstring> 3 typedef long long LL; 4 5 const int N = 1000010; 6 const LL MO = 1000000007; 7 const LL phi = 1000000006; 8 9 char pn[N], pm[N]; 10 LL a, b, c, d, m, n; 11 12 inline LL qpow(LL A, LL B) { 13 LL ans = 1; 14 A %= MO; 15 while(B) { 16 if(B & 1) { 17 ans = ans * A % MO; 18 } 19 A = A * A % MO; 20 B = B >> 1; 21 } 22 return ans; 23 } 24 25 inline LL getsum(char *A, LL p) { 26 int len = strlen(A); 27 LL ans = 0; 28 for(int i = 0; i < len; i++) { 29 ans = ((ans << 3) + (ans << 1) + A[i] - 48) % p; 30 } 31 return ans; 32 } 33 34 inline LL Qget(LL a1, LL q, char *A) { 35 a1 %= MO; 36 q %= MO; 37 if(q == 1) { 38 m = getsum(A, MO); 39 m = ((m - 1) % MO + MO) % MO; 40 return m * a1 % MO; 41 } 42 //return a1 * (qpow(q, n) - 1) / (q - 1); 43 m = getsum(A, MO - 1); 44 m = ((m - 1) % (MO - 1) + (MO - 1)) % (MO - 1); 45 LL t = ((qpow(q, m) - 1) % MO + MO) % MO; 46 LL inv = qpow(q - 1, MO - 2); 47 return a1 * t % MO * inv % MO; 48 } 49 50 int main() { 51 scanf("%s", pn); 52 scanf("%s", pm); 53 scanf("%lld%lld%lld%lld", &a, &b, &c, &d); 54 55 //LL s = qpow(a, n - 1); 56 m = getsum(pm, phi); 57 m = ((m - 1) % phi + phi) % phi; 58 LL s = qpow(a, m); 59 LL t = Qget(b, a, pm); 60 //printf("%lld %lld %lld %lld \n", s, t, s * c, c * t + d); 61 62 //LL ss = qpow(s, m - 1); 63 n = getsum(pn, phi); 64 n = ((n - 1) % phi + phi) % phi; 65 LL ss = qpow(s * c, n); 66 LL tt = Qget(d + t * c, s * c, pn); 67 //printf("%lld %lld \n", ss, tt); 68 69 LL ans = s * (ss + tt) % MO + t; 70 printf("%lld", ans % MO); 71 72 return 0; 73 }
