用拉格朗日乘子法求解带约束最优化问题

 

 

 

 

 

 

 

 

# -*- coding: utf-8 -*-
#导入sympy包，用于求导，方程组求解等等
from sympy import * 
 
#设置变量
x1 = symbols("x1")
x2 = symbols("x2")
alpha = symbols("alpha")
beta = symbols("beta")
 
#构造拉格朗日等式
L = (x1-7/4)*(x1-7/4) + (x2-5/2)*(x2-5/2) + alpha*(5-x1-x2) + beta*(x1+x2*x2-5*x2)
 
#求导，构造KKT条件
difyL_x1 = diff(L, x1)  #对变量x1求导
difyL_x2 = diff(L, x2)  #对变量x2求导
difyL_beta = diff(L, beta)  #对乘子beta求导
dualCpt = alpha * (5-x1-x2)  #对偶互补条件
 
#求解KKT等式
aa = solve([difyL_x1, difyL_x2, difyL_beta, dualCpt], [x1, x2, alpha, beta])
 
#打印结果，还需验证alpha>=0,x1>=0,x2>=0和不等式约束<=0
for i in aa:
    if i[2]>=0 and i[0] >= 0 and i[1]>=0:
        if (i[0]+i[1]-5) >= 0:
            print(i)
            

'''    output
(2.25000000000000, 4.50000000000000, 0.0, -1.00000000000000)
(4.00000000000000, 1.00000000000000, 2.62500000000000, -1.87500000000000)
(6.25000000000000, 2.50000000000000, 0.0, -9.00000000000000)
'''

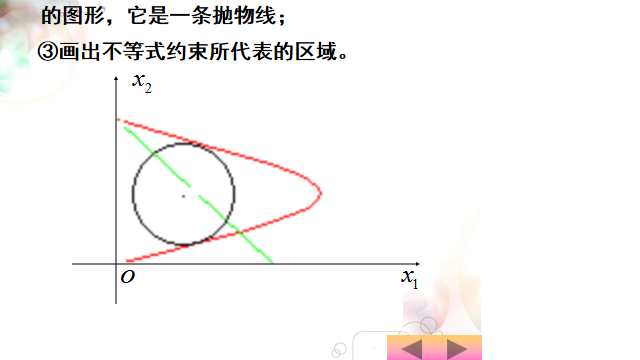
求出的三个极点分别为目标圆与抛物线上半相切，与直线和抛物线相交，与抛物线顶点相切

其中（9/4,9/2）时取得极小值

 

参考：

1.浅谈拉格朗日乘子法

2.Python科学计算利器——SymPy库

3.使用Python求解带约束的最优化问题详解