EPNP主要是利用已知的3d点,通过PCA选择4个控制点,建立新的局部坐标系,从而将3d坐标用新的控制点表示出来。
然后,利用相机投影模型和2d点,转换到相机坐标系中,再在相机坐标系中建立和世界坐标系同样关系(每个点在相机坐标系和世界坐标系下控制点处的坐标一致)的4个控制点,求解出相机坐标系下的四个控制点的坐标,进而利用ICP求解pose。
一、根据3d点,找到质点,同时利用PCA,找出三个主轴方向后,求出每个3d点在四个控制点上对应αij的值。
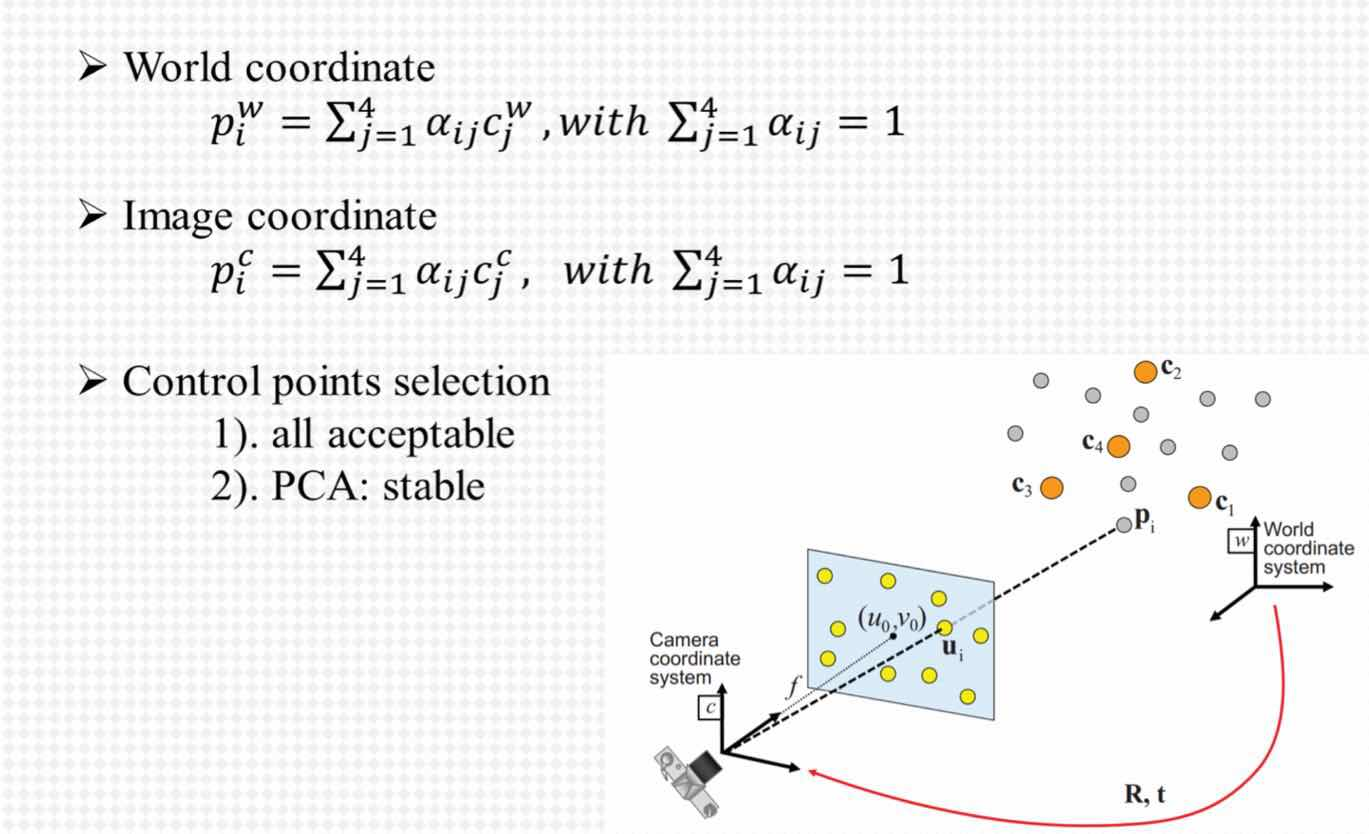
二、利用针孔相机投影模型,将相机坐标系下的3d坐标投影到2d坐标,然后将相机坐标系下的3d坐标转换成在相机坐标系下四个控制点下的坐标值。
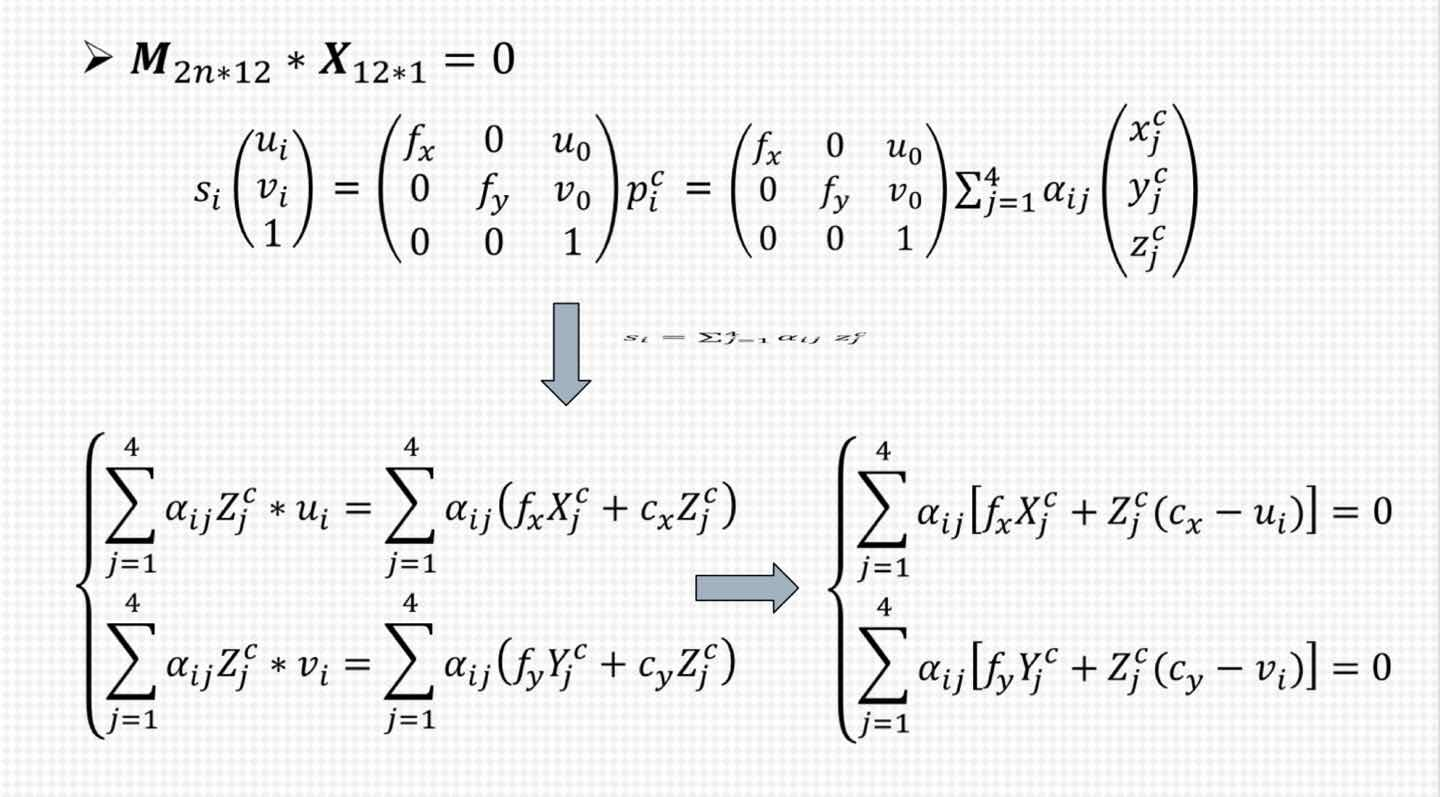
注:为了求取2d点到相机坐标系内的坐标,假设相机坐标系内的坐标在相机坐标系下的四个控制点的坐标等于在世界坐标系下的四个控制点的坐标,即αij一致,这样相当于求取四个控制点的旋转和平移。所以,上图的未知数就是在相机坐标系下的四个控制点的坐标值,已知的是相机内参、αij。所以是一个2n*12 *12*1的方程组。
三、对M进行SVD分解,求出相机坐标系下的四个控制点的坐标值
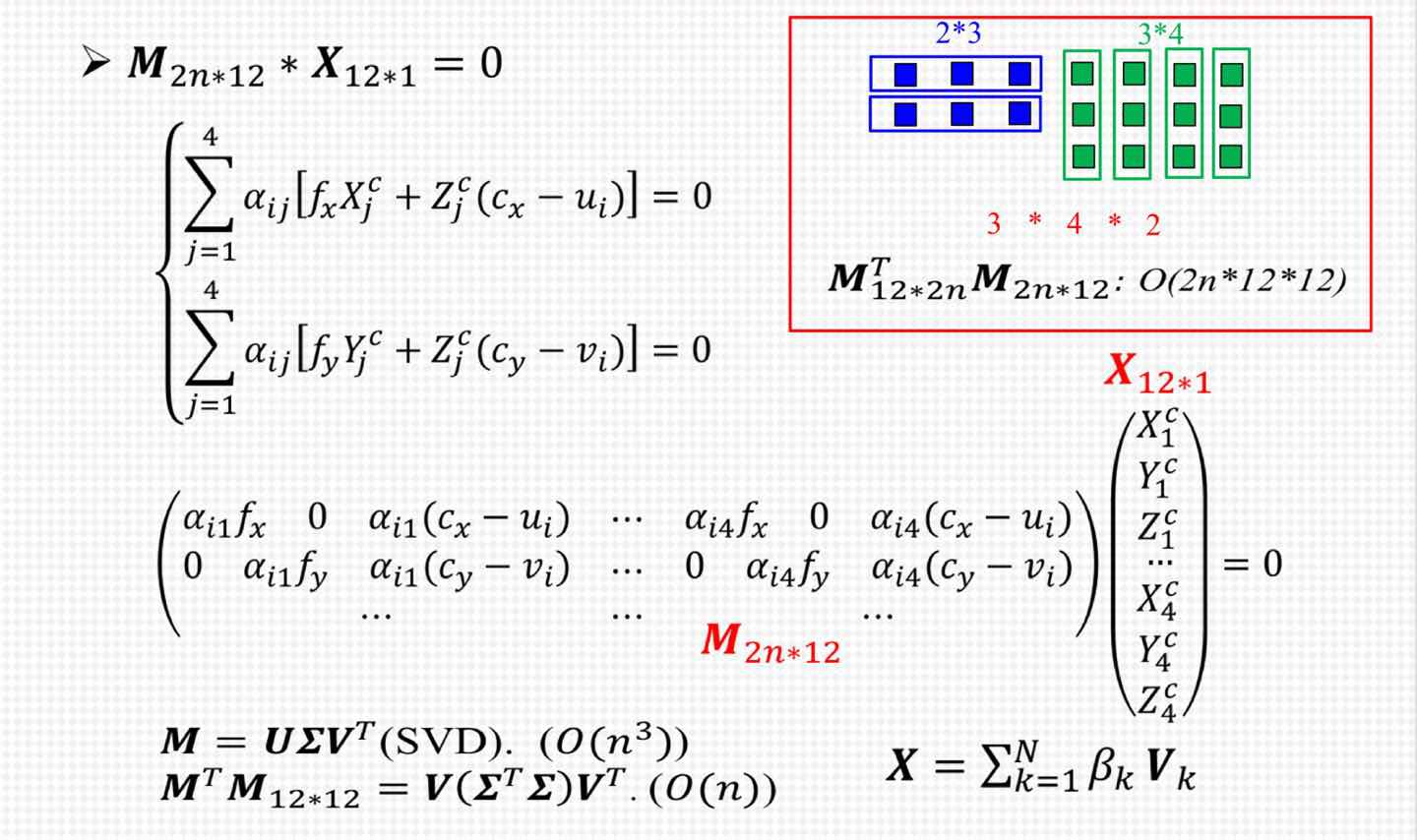
这里出现了一个欠约束的问题,如果匹配点是大于等于6对,则之间取V的最后一列向量,如果小于6对时,需要取V的倒数4列向量的组合作为四个控制点的坐标值。
四、针对相机坐标系下四个控制点的取值向量不同,求取βk
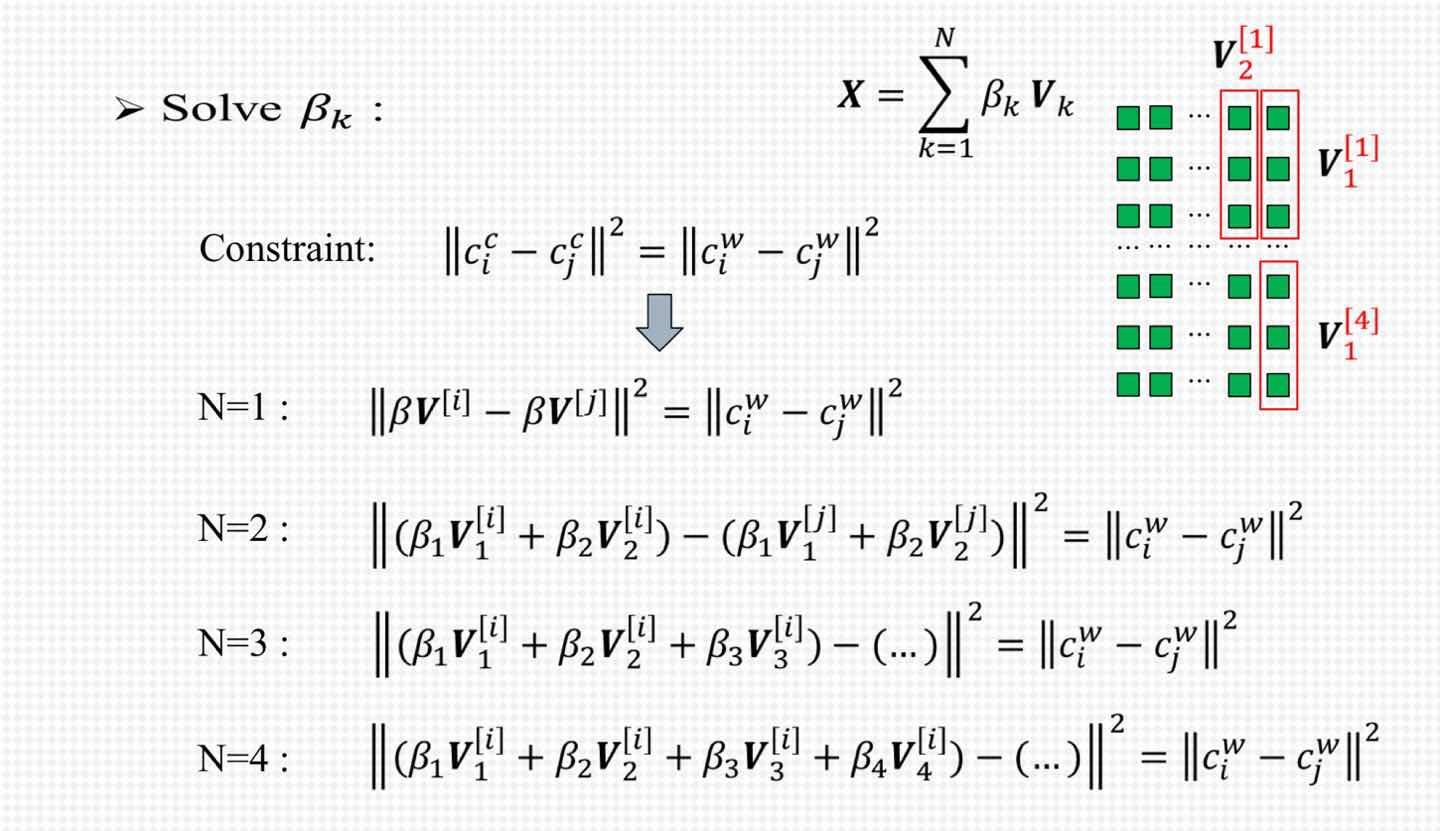
N=1-3的情况比较简单,是线性方程组求解的范畴,N=4是一个欠定方程,需要利用重线性化和子集近似的思想 :

五、将求取出来的相机坐标系控制点坐标和世界坐标系控制点坐标进行高斯牛顿最小化

六、求出了相机坐标系的控制点后,利用ICP求解R,t

七、cue流程





