快速傅里叶变换（FFT）求解多项式乘法

在我还会FFT的时候赶快写下一篇博客留着以后看。。。。。。

FFT是用来求解多项式乘法，那么首先我们要知道多项式是啥。

\[A(x) = a_0+a_1x^1+a_2x^2+···+a_{n-1}x^{n-1} \]

这是个n-1次多项式（最高项是\(x^{n-1}\)），\(a_0,a_1,···a_{n-1}\)是它各项的系数，该多项式可以写成：

\[A(x) = \sum_{j=0}^{n-1}a_jx^j \]

一个多项式可以通过一组系数所确定，而这组系数所组成的向量也叫做系数向量（如\(A(x)\)的系数向量为：[\(a_0 \ \ \ a_1\ ··· \ a_{n-1}\)]），通过系数向量表示一个多项式的方式叫做系数表示法

多项式乘法就是，我们已知两个多项式：\(A(x),B(x)\)，分别是n-1次和m-1次多项式。

\[A(x) = \sum_{j = 0}^{n - 1}a_jx^j\\ B(x) = \sum_{j = 0}^{m-1}b_jx^j \]

现在讲这两个多项式相乘，得到一个最高n+m-1次多项式：

\[C(x) = \sum_{j = 0}^{n+m-1}c_jx^j \]

那么求解\(C(x)\)也就是求出它的系数向量：[\(c_0 \ \ c_1 \ \ ··· \ \ c_j \ \ ··· \ \ c_n+m-1\)]

如果直接遍历\(A(x),B(x)\)的每一项的话是\(O(n*m)\)，我们需要更快的算法，就是我们所讨论的：快速傅里叶变换(FFT)

前置芝士：

点值表示法

对于一个已知的多项式\(A(x)\)，将\(x_0\)代入可以得到一个确定的\(y_0\)，并且，可以将\((x_0,y_0)\)看做是坐标系上的一个点。进一步可以将任意多的互不相等的自变量代入\((x_1,x_2,···)\)，从而得到更多的点：\((x_1,y_1),(x_2,y_2),···\)

我们知道，通过两个（不同的）点，可以解析一次多项式\((ax+b)\)，通过三个不同的点可以解析二次多项式\((ax^2+bx+c)\)，所以可以进一步的推出，通过n+1个不同的点，可以解出n次多项式

通过n+1个不同的点\(\left\{ (x_1,y_1),(x_2,y_2),··· \right\}\)，唯一确定一个n次多项式，该方式也叫做多项式的点值表示法

我们惊奇的发现两个用点值表示的多项式相乘，复杂度是\(O(n)\)的！具体方法：\(C(x_i)=A(x_i)×B(x_i)\)，所以O\((n)\)枚举\(x_i\)即可。

要是我们把两个多项式转换成点值表示，再相乘，再把新的点值表示转换成多项式岂不就可以\(O(n)\)解决多项式乘法了！

……很遗憾，显然，把多项式转换成点值表示的朴素算法是\(O(n^2)\)的。另外，即使你可能不会——把点值表示转换为多项式的朴素“插值算法”也是\(O(n^2)\)的。

但是可以发现，大整数乘法复杂度的瓶颈可能在“多项式转换成点值表示”这一步（以及其反向操作），只要完成这一步就可以\(O(n)\)求答案了。如果能优化这一步就可以了。

于是乎介绍另外两个前置芝士

离散傅里叶变换（DFT）以及离散傅里叶变换逆变换（IDFT），公式如下：

\[X_k = \sum_{j = 0}^{n-1}x_je^{\frac{2\pi i}{n}kj} (DFT)\\ X_j = \frac{1}{n}\sum_{k = 0}^{n-1}X_ke^{\frac{-2\pi i}{n}jk}(IDFT) \]

上面的两个式子中\(i\)是虚根（\(i^2 = -1\)），关于这两个式子的证明在文章最后会给出。

我们设置一些变量，将这两个公式代入到我们之前的问题里。

设：\(w = e^{\frac{2\pi i}{N}}\)，其中\(N = n+m\)，关于变量\(w\)的性质先不讨论，之后会有，再令

\[c_j = f(j),C_k = C(w^k) \]

将这些变量代入到DFT的公式里可得到：

\[C_k = C(w^k)=\sum_{j = 0}^{N-1}c_j(w^k)^j= \sum_{j=0}^{N-1}c_je_{\frac{2\pi i}{N}kj} \]

通过上式讲DFT与我们目标多项式\(C(x)\)关联了起来，自然也就可以通过IDFT来计算多项式的系数\(c_j\)：

\[c_j = \frac{1}{N}\sum_{k=0}^{N-1}C_k(w^{-j})^k=\frac{1}{N}\sum_{k=0}^{N-1}C_ke^{-\frac{2\pi i}{N}jk} \]

但是，由于不知道\(c_j\)的具体值（知道就完结撒花了），所以无法用DFT计算\(C(w^k)\)

不过，我们知道：\(C(x)=A(x)*B(x)\)，而且多项式\(A(x)B(x)\)的系数是已知的，所以可以“曲线救国”：

\[C(w^k)= A(w^k)*B(w^k) \]

通过该式计算\(C(w^k)\)，然后再使用IDFT计算\(c_j\)。

以上是FFT的概括，下面进行展开讨论

一个芝士：N次单位根

为了更好的讨论\(w = e^{\frac{2\pi i}{N}}\)，我们还是从欧拉公式说起

\[e^{i\theta} = \cos\theta+i\sin\theta \]

该公式的证明也在文章最后给出。

\(e^{i\theta}\)是一个复数，他的实部的值为\(\cos\theta\)，虚部的值为\(\sin\theta\)，所以，\(e^{i\theta}\)对应复数平面上的点与原点之间的距离恒为1，如图

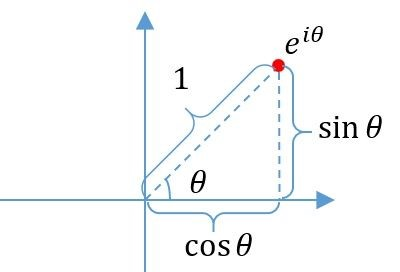
因为\(\sin\theta,\cos\theta\)是周期函数（周期为\(2\pi\)），所以可以得出：

\[e^{i(\theta+2\pi)=e^{i\theta}} \]

并且无论\(\theta\)取何值，\(e^{i\theta}\)都是分布在复平面的单位圆上，由于是单位元，所以\(\theta\)此时就等于是从1（起点）到\(e^{i\theta}\)在圆上的弧长。

上面简要介绍了欧拉公式，下面回到我们定义的变量：\(w = e^{\frac{2 \pi i}{n}}\)，前面的概述中为了方便，\(w\)没有加上下标，在此为更清楚的表示会给\(w\)加一个下标：\(w_n=e^{\frac{2\pi i}{n}}\)

从面欧拉公式的讨论中可以指导，\(e^{2\pi i} = 1\)，相当于在单位圆上绕了一圈又回到了起点，而\(\frac{2\pi}{n}\)相当于是这个单位圆分成了\(n\)等分，而\(w_n^k\)就对应单位圆上第\(k\)个等分点（\(k=0,1,2,···，n-1\)）

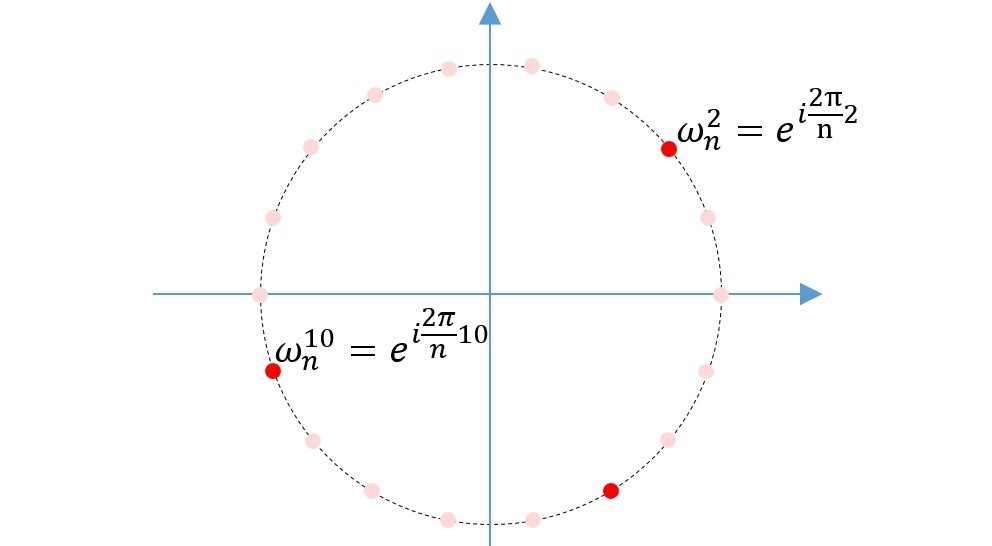
这是个\(n=18\)的例子，并标出了两个值\(\left\{ w_n^k|k=2,10 \right\}\)，通过前面的讨论以及这个栗子，应该对\(w_n^k\)有了一个比较直观的认识，说了这么多，应该能猜到N次单位根就是指的它了，关于N次单位根介绍几个性质：

\[1. \ \ w_n^{k+\frac{n}{2}}=e^{\frac{2\pi i}{n}(k+\frac{n}{w})}=e^{\frac{2\pi i}{n}k}e^{i\pi} =w_n^k(\cos\pi+i\sin\pi)=-w_n^k \\2. \ \ w_{2n}^{2k} = w_n^k \\3. \ \ w_n^{-k} = 1·e^{\frac{i2\pi}{n}(-k)} = e^{2\pi i}e^{\frac{2 \pi i}{n}(-k)}=e^{\frac{2\pi i}{n}(n-k)}=w_n^{n-k} \]

性质1是消去引理，性质2是折半引理，性质3我忘了叫啥。。。

计算\(C(w_N^k)\)

首先，定义\(N = m+n\)（n,m分别是多项式\(A(x),B(x)\)的系数数量），前面已经说过无法直接使用DFT计算\(C(w_n^k)\)，需要先计算\(A(w_N^k),B(w_N^k)\)

单数如果直接把\(\left\{ w_N^k|k=0,1,2,···，N-1 \right\}\)简单粗暴的代进去，时间复杂度依旧是\(O(N^2)\)，无论后面如何计算，也无法降低整个算法的复杂度，因为，需要使用的一些方法，来降低\(A(w_N^k),B(w_N^k)\) 的时间

for example，我们有个多项式：

\[H(x) = h_0+h_1x^1+h_2x^2+h_3x^3 \]

我们可以将它的奇数项与偶数项分开：

\[H(x)=(h_0+h_2x^2)+(h_1x^1+h_3x^3)=(h_0+h_2x^2)+x(h_1+h_3x^2)\\= H1(x^2)+xH2(x^2) \]

并且\(H1(x),H2(x)\)还可以递归的计算下去，该方法用到\(A(x),B(x)\)上就是：

\[A(x) = A1(x^2)+xA2(x^2)B(x) = B1(x^2)+xB2(x^2) \]

时间复杂度就变成了：

\[T(n) = 2T(\frac{n}{2})+O(n)=O(nlogn) \]

除此之外，还可以利用前面讨论的单位根的性质来降低计算量，例如，\(0 \leq k < \frac{n}{2}\)：

\[A(w_n^k) = A1(w_n^{2k})+w_n^kA2(w_n^{2k})=A1(w_{\frac{n}{2}}^k)+w_n^kA2(w_{\frac{n}{2}}^k)\\A(w_n^{k+\frac{n}{2}}) = A1(w_n^{2k+n})+w_n^{k+\frac{n}{2}}A2(w_n^{2k+n}) = A1(w_n^{2k})-w_n^kA2(w_n^{2k}) \\= A1(w_{\frac{n}{2}}^k)-w_n^kA2(w_{\frac{n}{2}}^k)) \]

这样，计算\(k\)一般的取值范围就可以得到整个取值范围的结果，所以，将\(A(w_N^k),B(w_N^k)\)计算完毕之后，就可以通过简单的乘法来计算\(C(w_N^k)\)：

\[C(w_N^k) = A(w_N^k)B(w_N^k),k=0,1,2,···，N-1 \]

求解\(C(x)\)系数

计算 这一步基本已经完成一大半了，只需要使用IDFT公式来求解\(C(x)\)的各项系数就可以了：

\[c_j = \frac{1}{N}\sum_{k=0}^{N-1}C_ke^{-\frac{2\pi i}{N}jk} = \frac{1}{N}\sum_{k=0}^{N-1}C_k(e^{-\frac{2\pi i}{N}j})^k=\frac{1}{N}\sum_{k=0}^{N-1}C_k(w_N^{-j})^k \]

上面式子中\(C_k = C(w_N^k)\)，另外，为了方面表示，通常会构造一个N-1次多项式\(D(x)\)，它的系数就是各个\(C_k\)的值：

\[D(x) = C_0 + C_1x^1+C_2x^2+···+C_{N-1}x^{N-1} = \sum_{k=0}^{N-1}C_kx^k \]

所以，最终\(c_j\)的计算公式可以写成：

\[c_j = \frac{1}{N}\sum_{k=0}^{N-1}C_k(w_N^{-j})^k=\frac{1}{N}\sum_{k=0}^{N-1}C_k(w_N^{N-j})^k=\frac{1}{N}D(w_N^{N-j}) \]

上式第二部使用了单位根的性质3：

\[c_0 = \frac{1}{N}D(w_N^{N-0}) = \frac{1}{N}D(w_N^N)=\frac{1}{N}D(w_N^0) \]

总结

1.取N个单位根：[\(w_N^0 \ \ w_N^1 \ \ w_N^2 \ \ ··· \ \ w_N^{N-1}\)]

2.将它们分别代入到多项式\(A(x),B(x)\)中

3.计算\(C(w_N^k) = A(w_N^k)B(w_N^k)\)

4.构造一个新的多项式\(D(x) = C_0+C_1x^1+C_2x^2+···+C_{N-1}x^{N-1}\)

5.计算\(D(w_N^k)\)

6.计算多项式\(C(x)\)的系数\(c_j=\frac{1}{N}D(w_N^{N-j}),j=0,1,2,···，N-1\)

at last（未完待续）

• 欧拉公式证明
• DFT与IDTF证明