最大流

概述

我们有一张图，要求从源点流向汇点的最大流量（可以有很多条路到达汇点），就是我们的最大流问题。

Ford-Fulkerson增广路算法

该方法通过寻找增广路来更新最大流，有EK,dinic,SAP,ISAP主流算法。

求解最大流之前，我们先认识一些概念。

残量网络

首先介绍一下一条边的剩余容量\(c_f(u,v)\)，他表示的是这条边的容量与流量之差，即\(c_f(u,v) = c(u,v) - f(u,v)\)

对于流函数\(f\)，残存网络\(G_f\)是网络\(G\)中所有结点和剩余容量大于0的边构成的子图。形式化的定义，即\(G_f = (V_f = V,E_f = \left\{ (u,v) \in E,c_f(u,v) > 0 \right\})\)

注意，剩余容量大于0的边可能不存在原图\(G\)中（根据容量、剩余容量的定义以及流函数的斜对称性得到）。可以理解为，残量网路中包括了那些还剩了流量空间的边构成的图，也包括反向边。

增广路

在原图\(G\)中若一条从源点到汇点的路径上所有边的剩余容量都大于0，这条路被称为增广路

或者说，在残存网络\(G_f\)中，一条从源点到汇点的路径被称为增广路。

此处应该有图片

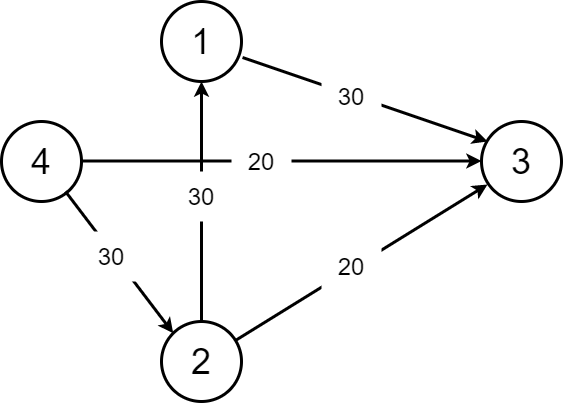
我们从4到3，肯定可以先从流量为20的这条边先走，那么这条边就被走掉了，不能再选，总的流量为20（目前为止）。然后我们可以这样选择：

• \(4\rightarrow2\rightarrow3\)这条增广路的总流量为20。到2的时候还是30，到3了就只有20了。
• \(4\rightarrow2\rightarrow1\rightarrow3\)这样我们就很好的保留了30的流量

所以我们这张图的最大流就应该是20+30=50。

求最大流有几种方法。

Edmond-Karp 动能算法（EK 算法）

这个算法就是bfs找增广路，然后对其进行增广。

• 我们从源点一直bfs走来走去，碰到汇点就停，然后增广（每一条路都要增广）我们在bfs的时候就注意一下流量合不合法就可以了
• 增广：按照我们找的增广路再重新走一遍，走的时候把这条流的能构成的最大流量减一减，然后给答案加上最小流量就可以了。

反向边：增广的是偶要注意建造反向边，原因是这条路不一定是最优的，这样子程序可以进行反悔，假如我们对这条路进行增广了，那么其中的每一条边的反向边的流量就是它的流量。

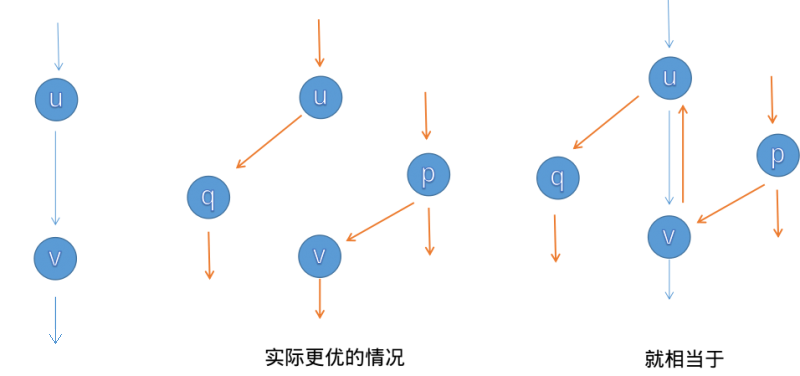
一些小细节：

如果用邻接矩阵的话，反向边直接就是从\(table[x,y]\)变成\(table[y,x]\)。如果用链前，那么在假如边的时候就要先假如反向边。那么在用的时候，我们直接\(i\operatorname{xor}1\)就可以了（\(i\)为边的编号）。我们在加入正向边后加入反向边，就是靠近的，所以可以使用\(\operatorname{xor}\)。我们还要注意一开始的编号要设置为\(tot=1\)，因为边要从编号2开始，这样子\(\operatorname{xor}\) 对编号2,3的边才有效果。

EK算法的时间复杂度为\(O(nm^2)\)（其中\(n\)为点数，\(m\)为边数）效率还有很大的提升空间。

#define maxn 250
#define INF 0x3f3f3f3f

struct Edge {
  int from, to, cap, flow;
  Edge(int u, int v, int c, int f) : from(u), to(v), cap(c), flow(f) {}
};

struct EK {
  int n, m;
  vector<Edge> edges;
  vector<int> G[maxn];
  int a[maxn], p[maxn];

  void init(int n) {
    for (int i = 0; i < n; i++) G[i].clear();
    edges.clear();
  }

  void AddEdge(int from, int to, int cap) {
    edges.push_back(Edge(from, to, cap, 0));
    edges.push_back(Edge(to, from, 0, 0));
    m = edges.size();
    G[from].push_back(m - 2);
    G[to].push_back(m - 1);
  }

  int Maxflow(int s, int t) {
    int flow = 0;
    for (;;) {
      memset(a, 0, sizeof(a));
      queue<int> Q;
      Q.push(s);
      a[s] = INF;
      while (!Q.empty()) {
        int x = Q.front();
        Q.pop();
        for (int i = 0; i < G[x].size(); i++) {
          Edge& e = edges[G[x][i]];
          if (!a[e.to] && e.cap > e.flow) {
            p[e.to] = G[x][i];
            a[e.to] = min(a[x], e.cap - e.flow);
            Q.push(e.to);
          }
        }
        if (a[t]) break;
      }
      if (!a[t]) break;
      for (int u = t; u != s; u = edges[p[u]].from) {
        edges[p[u]].flow += a[t];
        edges[p[u] ^ 1].flow -= a[t];
      }
      flow += a[t];
    }
    return flow;
  }
};

Dinic算法

每次增广前，我们先用bfs来讲图分层，设源点的层数为0，那么一个点的层数便是它离源点的最近距离。

通过分层，我们可以干两件事：

• 如果不存在到汇点的增广路
• 确保我们找到的增广路时最短的

接下来是dfs找增广路的过程

我们每次找增广路的时候，都只找比当前点层数多1的点进行增广（这样就可以确保我们找到的增广路是最短的）

Dinic算法有两个优化：

• 多路增广：每次找到一条增广路的时候，如果残余流量没有用完，我们可以利用残余部分流量，再找出一条增广路。这样就可以在一次DFS中找出多条增广路，大大提高了算法的效率。
• 当前弧优化：如果一条边已经被增广过，那么它就没有可能被增广第二次。那么，我们下一次进行增广的时候，就可以不必再走那些已经被增广过的边。

设点数为\(n\)，边数为\(m\)，那么Dinic算法的时间复杂度是\(O(n^2m)\)，在稀疏图上效率跟EK相当，在稠密图上效率比EK高很多。

特别的，在求解二分图最大匹配问题时，可以证明Dinic算法的时间复杂度是\(O(m\sqrt{n})\)

#define maxn 250
#define INF 0x3f3f3f3f

struct Edge {
  int from, to, cap, flow;
  Edge(int u, int v, int c, int f) : from(u), to(v), cap(c), flow(f) {}
};

struct Dinic {
  int n, m, s, t;
  vector<Edge> edges;
  vector<int> G[maxn];
  int d[maxn], cur[maxn];
  bool vis[maxn];

  void init(int n) {
    for (int i = 0; i < n; i++) G[i].clear();
    edges.clear();
  }

  void AddEdge(int from, int to, int cap) {
    edges.push_back(Edge(from, to, cap, 0));
    edges.push_back(Edge(to, from, 0, 0));
    m = edges.size();
    G[from].push_back(m - 2);
    G[to].push_back(m - 1);
  }

  bool BFS() {
    memset(vis, 0, sizeof(vis));
    queue<int> Q;
    Q.push(s);
    d[s] = 0;
    vis[s] = 1;
    while (!Q.empty()) {
      int x = Q.front();
      Q.pop();
      for (int i = 0; i < G[x].size(); i++) {
        Edge& e = edges[G[x][i]];
        if (!vis[e.to] && e.cap > e.flow) {
          vis[e.to] = 1;
          d[e.to] = d[x] + 1;
          Q.push(e.to);
        }
      }
    }
    return vis[t];
  }

  int DFS(int x, int a) {
    if (x == t || a == 0) return a;
    int flow = 0, f;
    for (int& i = cur[x]; i < G[x].size(); i++) {
      Edge& e = edges[G[x][i]];
      if (d[x] + 1 == d[e.to] && (f = DFS(e.to, min(a, e.cap - e.flow))) > 0) {
        e.flow += f;
        edges[G[x][i] ^ 1].flow -= f;
        flow += f;
        a -= f;
        if (a == 0) break;
      }
    }
    return flow;
  }

  int Maxflow(int s, int t) {
    this->s = s;
    this->t = t;
    int flow = 0;
    while (BFS()) {
      memset(cur, 0, sizeof(cur));
      flow += DFS(s, INF);
    }
    return flow;
  }
};

ISAP

这个算法我不会w