最近公共祖先
倍增求LCA
① 初始化: 通过
bfs初始化两个数组depth[],fa[]\(\quad\) \(\quad\)
depth[n]: 表示深度(到根节点的距离加1)\(\quad\) \(\quad\)
fa[i][j]: 表示从i开始, 向上走 \(2^j\) 步所能到的节点编号 (\(0 \leqslant j \leqslant log_2n\))\(\quad\) \(\quad\) \(\quad\) \(\quad\) \(\quad\) \(\quad\)
fa[i,0]=i的父节点
\(\quad\) \(\quad\) \(\quad\) \(\quad\) \(\quad\) \(\quad\)fa[i,j]=fa[fa[i,j-1],j-1]\(\quad\) \(\quad\) 哨兵: 如果从
i开始跳 \(2^j\) 步会跳过根节点, 那么fa[i,j] = 0,depth[0] = 0② 查询
\(\quad\) \(\quad\) [1] 先将两个点跳到同一层
\(\quad\) \(\quad\) [2] 让两个点同时往上跳, 一直跳到它们的最近公共祖先的下一层
//倍增法求最近公共祖先算法模板
int h[N],e[M],ne[M],idx;
int depth[N],fa[N][size]; //size取logn(n为节点数量)
int q[N];
//宽搜预处理depth和fa数组
void bfs (int root)
{
memset(depth,0x3f,sizeof depth);
depth[0]=0,depth[root]=1;
int hh=0,tt=0;
q[0]=root;
while(hh<=tt)
{
int t=q[hh++];
for(int i=h[t];i!=-1;i=ne[i])
{
int j=e[i];
if(depth[j]>depth[t]+1)
{
depth[j]>depth[t]+1;
q[++tt]=j;
fa[j][0]=t;
for(int k=1;k<=size;k++)
fa[j][k]=fa[fa[j][k-1]][k-1];
}
}
}
}
//查询节点a,b的最近公共祖先
int lca (int a,int b)
{
if(depth[a]<depth[b])swap(a,b);
for(int k=size;k>=0;k--)
if(depth[fa[a][k]]>=depth[b])
a=fa[a][k];
if(a==b)return a;
for(int k=size;k>=0;k--)
if(fa[a][k]!=fa[b][k])
{
a=fa[a][k];
b=fa[b][k];
}
return fa[a][0];
}
Tarjan——离线求LCA
在深度优先遍历时, 将所有点分为三大类:
(1) 已经遍历过且回溯过的点, 标记为2
(2) 正在搜索的分支上的点, 标记为1
(3) 还未搜索到的点, 标记为0
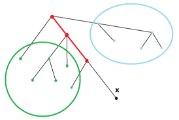
如果当前正在搜索上图中的点
x, 则找一下所有和这个点x相关的询问, 假设询问x和y的最近公共祖先, 如果点y在绿色圈中, 则可以得到x和y的LCA是图中对应的红色实心点; 如果y还没被搜索到, 则直接忽略即可, 后面的遍历过程中遍历到点y时, 就会处理这个询问
因此我们可以使用并查集将所有标记为
2的点合并到它们对应的红色实心节点中, 当我们需要查看x和某个绿色圈中的点y的LCA时, 只需要查看一下点y合并到了哪个点中即可
//Tarjan离线求LCA算法模板
int n,m; //n为节点数,m为询问数量
int h[N],e[M],ne[M],w[M],idx;
int p[N];
int ans[M]; //ans[i]记录第i个询问的LCA的值
int st[N]; //标记每个节点的状态0/1/2
vector<pair<int,int>> query[M]; //记录询问,first存查询的另外一个点,second存查询编号
//并查集操作
int find (int x)
{
if(p[x]!=x)p[x]=find(p[x]);
return p[x];
}
//tarjan操作求每个询问
void tarjan (int u)
{
st[u]=1; //正在搜索分支上的点,标记为1
for(int i=h[u];i!=-1;i=ne[i])
{
int j=e[i];
if(!st[j])
{
tarjan(j);
p[j]=u;
}
}
for(auto item: query[u]) //遍历所有和这个点有关的询问
{
int y=item.first,id=item.second;
if(st[y]==2)ans[id]=find(y);
}
st[u]=2; //已经遍历过且回溯过的点,标记为2
}
//主函数,记录所有询问到query[][]中
int main()
{
for(int i=0;i<m;i++)
{
int a,b;
cin>>a>>b;
query[a].push_back({b,i});
query[b].push_back({a,i});
}
for(int i=1;i<=n;i++)p[i]=i;
tarjan(1); //随便选其中一个节点作为根节点均可
for(int i=0;i<m;i++)cout<<ans[i]<<' ';
return 0;
}
树上差分
点权差分
f[i]表示点i的点权,w[i]表示i及其子树权值之和若给
[x,y]两点之间路径上所有点的权值+d, 点差分因为需要加上LCA点, 但左右起点到终点时会加两次, 所有在此点及其父节点各减一份f[x] += d,f[y] += d,f[lca(x,y)] -= d,f[fa[lca(x,y)]] -= d
边权差分
f[i]表示点i到其父节点的边权,w[i]表示i的子树权值之和若给
[x,y]两点之间路径上的所有边的权值+d, 边差分由于边数等于点数减一, 不计LCA点, 所以在此点减两份f[x] += d,f[y] += d,f[lca(x,y)] -= d*2
最后
DFS由底向上统计更新即可
//树上遍历dfs(由下往上)
void dfs (int u,int fa)
{
for(int i=h[u];i!=-1;i=ne[i])
{
int j=e[i];
if(j==fa)continue;
dfs(j,u);
f[u]+=f[j];
}
}
