二分算法

整数二分

二分与单调性的关系: 如果有单调性, 一定可以二分; 可以二分的题目, 不一定非得有单调性

二分的本质: 边界

在区间上定义了某种性质, 该性质在区间右半边满足, 左半边不满足, 使整个区间一分为二

二分可以寻找性质的边界(既可以寻找边界 i , 也可以寻找边界 j )

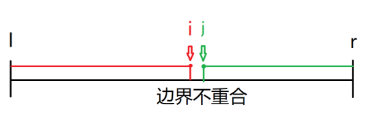
① 寻找边界 i :\(\quad\) \(\quad\) \(\quad\) \(\quad\) \(\quad\) mid = (l+r+1)/2

\[if(check(mid)) \begin{cases} true \quad [mid,r]:l=mid\\[2ex] false \quad [l,mid-1]:r=mid-1\\[2ex] \end{cases} \]

② 寻找边界 j : \(\quad\) \(\quad\) \(\quad\) \(\quad\) \(\quad\) mid = (l+r)/2

\[if(check(mid)) \begin{cases} true \quad [l,mid]:r=mid\\[2ex] false \quad [mid+1,r]:l=mid+1\\[2ex] \end{cases} \]

对 true : 更新左边界, 定义 mid 要上取整; 更新右边界, 定义 mid 要下取整, 防止陷入死循环

//整数二分算法模板1(寻找边界i)

int bsearch_1 (int l,int r)
{
    while(l<r)
    {
        int mid=(l+r+1)/2;
        if(check(mid))l=mid;
        else r=mid-1;
    }
    return l;
}

//整数二分算法模板2(寻找边界j)

int bsearch_2 (int l,int r)
{
    while(l<r)
    {
        int mid=(l+r)/2;
        if(check(mid))r=mid;
        else l=mid+1;
    }
    return l;
}

---

浮点数二分

因为浮点数没有整除, 所以不需要处理边界

需要时刻保证答案在区间内部

当区间长度很小的时候, 可以认为找到答案

//浮点数二分算法模板

double bsearch_3 (double l,double r)
{
    const double eps=1e-6;	
    //eps表示精度,取决于题目对精度的要求(一般取题目要求保留小数点后位数+2)
    
    while(r-l>eps)
    {
        double mid=(l+r)/2;
        if(check(mid))r=mid;
        else l=mid;
    }
    return l;
}