1.应用场景-最短路径问题
看一个应用场景和问题:
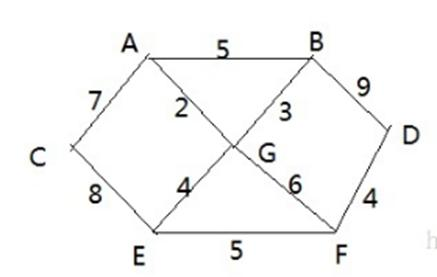
- 战争时期,胜利乡有 7 个村庄(A, B, C, D, E, F, G) ,现在有六个邮差,从 G 点出发,需要分别把邮件分别送到A, B, C , D, E, F 六个村庄
- 各个村庄的距离用边线表示(权) ,比如 A – B 距离 5 公里
- 问:如何计算出 G 村庄到 其它各个村庄的最短距离?
- 如果从其它点出发到各个点的最短距离又是多少?
2.迪杰斯特拉(Dijkstra)算法介绍
迪杰斯特拉(Dijkstra)算法是 典型最短路径算法,用于计算一个结点到其他结点的最短路径。它的主要特点是以起始点为中心向外层层扩展( 广度优先搜索思想),直到扩展到终点为止。
3.迪杰斯特拉(Dijkstra)算法过程
- 设置出发顶点为 v,顶点集合 V{v1,v2,vi...},v 到 V 中各顶点的距离构成距离集合 Dis,Dis{d1,d2,di...},Dis集合记录着 v 到图中各顶点的距离(到自身可以看作 0,v 到 vi 距离对应为 di)
- 从 Dis 中选择值最小的 di 并移出 Dis 集合,同时移出 V 集合中对应的顶点 vi,此时的 v 到 vi 即为最短路径
- 更新 Dis 集合,更新规则为:比较 v 到 V 集合中顶点的距离值,与 v 通过 vi 到 V 集合中顶点的距离值,保留值较小的一个(同时也应该更新顶点的前驱节点为 vi,表明是通过 vi 到达的)
- 重复执行两步骤,直到最短路径顶点为目标顶点即可结束
4.迪杰斯特拉(Dijkstra)算法最佳应用-最短路径

- 战争时期,胜利乡有 7 个村庄(A, B, C, D, E, F, G) ,现在有六个邮差,从 G 点出发,需要分别把邮件分别送到A, B, C , D, E, F 六个村庄
- 各个村庄的距离用边线表示(权) ,比如 A – B 距离 5 公里
- 问:如何计算出 G 村庄到 其它各个村庄的最短距离?
- 如果从其它点出发到各个点的最短距离又是多少?
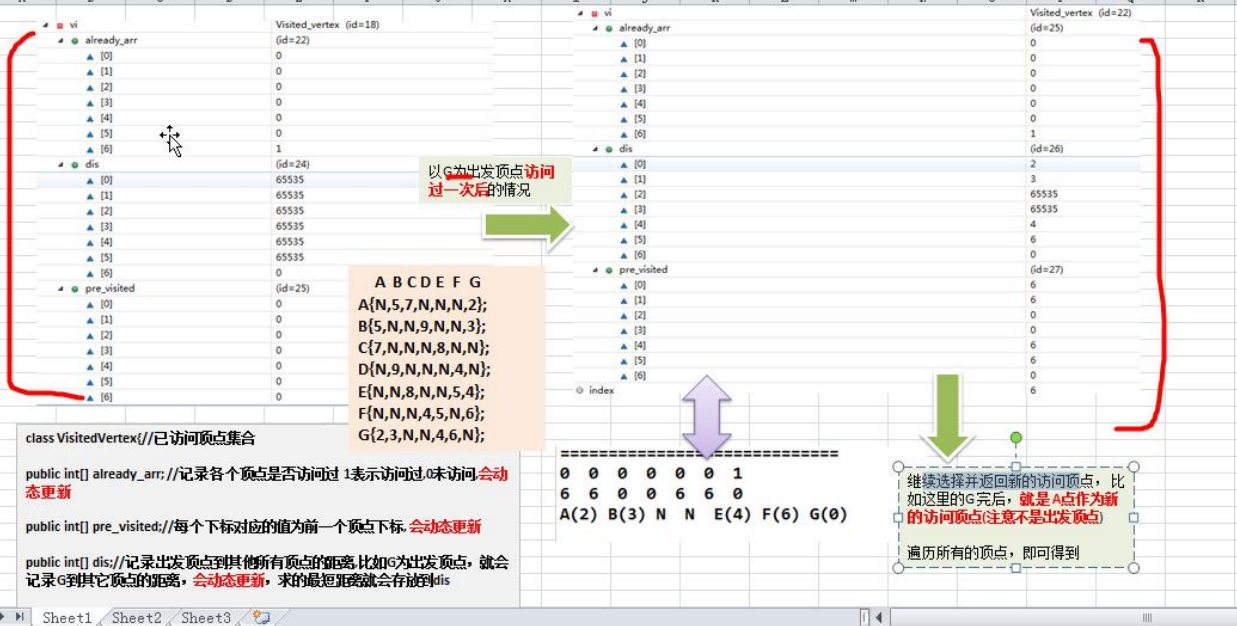
- 使用图解的方式分析了迪杰斯特拉(Dijkstra)算法 思路
![]()
- 代码实现
/**
* 迪杰斯特拉算法
*/
public class DijkstraAlgorithm {
static final int N = 65535;// 表示不可以连接
public static void main(String[] args) {
char[] vertex = {'A', 'B', 'C', 'D', 'E', 'F', 'G'};
//邻接矩阵
int[][] matrix = new int[vertex.length][vertex.length];
matrix[0] = new int[]{N, 5, 7, N, N, N, 2};
matrix[1] = new int[]{5, N, N, 9, N, N, 3};
matrix[2] = new int[]{7, N, N, N, 8, N, N};
matrix[3] = new int[]{N, 9, N, N, N, 4, N};
matrix[4] = new int[]{N, N, 8, N, N, 5, 4};
matrix[5] = new int[]{N, N, N, 4, 5, N, 6};
matrix[6] = new int[]{2, 3, N, N, 4, 6, N};
//创建 Graph 对象
Graph graph = new Graph(vertex, matrix);
//测试, 看看图的邻接矩阵是否 ok
graph.showGraph();
//测试迪杰斯特拉算法
graph.dsj(2);//C
graph.showDijkstra();
}
static class Graph {
private char[] vertex; // 顶点数组
private int[][] matrix; // 邻接矩阵
private VisitedVertex vv; //已经访问的顶点的集合
// 构造器
public Graph(char[] vertex, int[][] matrix) {
this.vertex = vertex;
this.matrix = matrix;
}
//显示结果
public void showDijkstra() {
vv.show();
}
// 显示图
public void showGraph() {
for (int[] link : matrix) {
System.out.println(Arrays.toString(link));
}
}
//迪杰斯特拉算法实现
/**
* @param index 表示出发顶点对应的下标
*/
public void dsj(int index) {
vv = new VisitedVertex(vertex.length, index);
update(index);//更新 index 顶点到周围顶点的距离和前驱顶点
for (int j = 1; j < vertex.length; j++) {
index = vv.updateArr();// 选择并返回新的访问顶点
update(index); // 更新 index 顶点到周围顶点的距离和前驱顶点
}
}
//更新 index 下标顶点到周围顶点的距离和周围顶点的前驱顶点,
private void update(int index) {
int len = 0;
//根据遍历我们的邻接矩阵的 matrix[index]行
for (int j = 0; j < matrix[index].length; j++) {
// len 含义是 : 出发顶点到 index 顶点的距离 + 从 index 顶点到 j 顶点的距离的和
len = vv.getDis(index) + matrix[index][j];
// 如果 j 顶点没有被访问过,并且 len 小于出发顶点到 j 顶点的距离,就需要更新
if (!vv.in(j) && len < vv.getDis(j)) {
vv.updatePre(j, index); //更新 j 顶点的前驱为 index 顶点
vv.updateDis(j, len); //更新出发顶点到 j 顶点的距离
}
}
}
}
// 已访问顶点集合
static class VisitedVertex {
// 记录各个顶点是否访问过 1 表示访问过,0 未访问,会动态更新
public int[] already_arr;
// 每个下标对应的值为前一个顶点下标, 会动态更新
public int[] pre_visited;
// 记录出发顶点到其他所有顶点的距离,比如 G 为出发顶点,就会记录 G 到其它顶点的距离,会动态更新,求的最短距离就会存放到 dis
public int[] dis;
//构造器
/**
* @param length :表示顶点的个数
* @param index: 出发顶点对应的下标, 比如 G 顶点,下标就是 6
*/
public VisitedVertex(int length, int index) {
this.already_arr = new int[length];
this.pre_visited = new int[length];
this.dis = new int[length];
//初始化 dis 数组
Arrays.fill(dis, 65535);
this.already_arr[index] = 1; //设置出发顶点被访问过
this.dis[index] = 0;//设置出发顶点的访问距离为 0
}
/**
* 功能: 判断 index 顶点是否被访问过
*
* @param index
* @return 如果访问过,就返回 true, 否则访问 false
*/
public boolean in(int index) {
return already_arr[index] == 1;
}
/**
* 功能: 更新出发顶点到 index 顶点的距离
*
* @param index
* @param len
*/
public void updateDis(int index, int len) {
dis[index] = len;
}
/**
* 功能: 更新 pre 这个顶点的前驱顶点为 index 顶点
*
* @param pre
* @param index
*/
public void updatePre(int pre, int index) {
pre_visited[pre] = index;
}
/**
* 功能:返回出发顶点到 index 顶点的距离
*
* @param index
*/
public int getDis(int index) {
return dis[index];
}
/**
* 继续选择并返回新的访问顶点, 比如这里的 G 完后,就是 A 点作为新的访问顶点(注意不是出发顶点)
*
* @return
*/
public int updateArr() {
int min = 65535, index = 0;
for (int i = 0; i < already_arr.length; i++) {
if (already_arr[i] == 0 && dis[i] < min) {
min = dis[i];
index = i;
}
}
//更新 index 顶点被访问过
already_arr[index] = 1;
return index;
}
//显示最后的结果
//即将三个数组的情况输出
public void show() {
System.out.println("==========================");
//输出 already_arr
for (int i : already_arr) {
System.out.print(i + " ");
}
System.out.println();
//输出 pre_visited
for (int i : pre_visited) {
System.out.print(i + " ");
}
System.out.println();
//输出 dis
for (int i : dis) {
System.out.print(i + " ");
}
System.out.println();
//为了好看最后的最短距离,我们处理
char[] vertex = {'A', 'B', 'C', 'D', 'E', 'F', 'G'};
int count = 0;
for (int i : dis) {
if (i != 65535) {
System.out.print(vertex[count] + "(" + i + ") ");
} else {
System.out.println("N ");
}
count++;
}
System.out.println();
}
}
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号