1.应用场景-背包问题
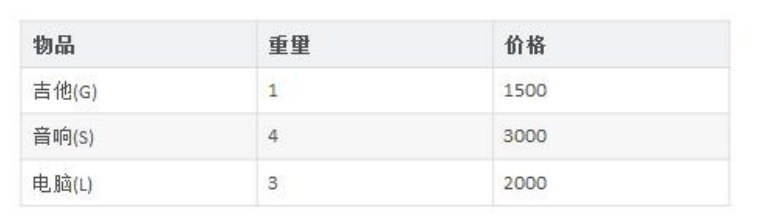
背包问题:有一个背包,容量为 4 磅 , 现有如下物品
-
要求达到的目标为装入的背包的总价值最大,并且重量不超出
-
要求装入的物品不能重复
2. 动态规划算法介绍
-
动态规划(Dynamic Programming)算法的核心思想是:将 大问题划分为小问题进行解决,从而一步步获取最优解的处理算法
-
动态规划算法与分治算法类似,其基本思想也是将待求解问题分解成若干个子问题,先求解子问题,然后从这些子问题的解得到原问题的解
-
与分治法不同的是,适合于用动态规划求解的问题,经分解得到 子问题往往不是互相独立的。 ( 即下一个子阶段的求解是建立在上一个子阶段的解的基础上,进行进一步的求解 )
-
动态规划可以通过填表的方式来逐步推进,得到最优解
3.动态规划算法最佳实践-背包问题
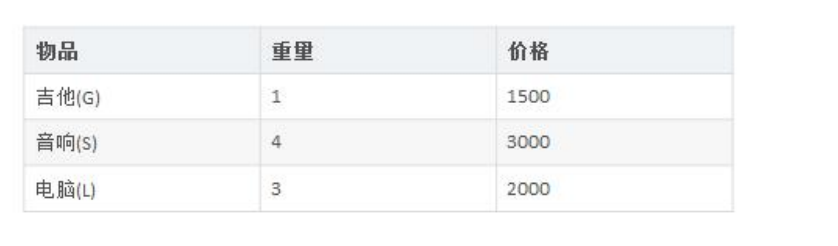
背包问题:有一个背包,容量为 4 磅 , 现有如下物品
-
要求达到的目标为装入的背包的总价值最大,并且重量不超出
-
要求装入的物品不能重复
思路分析和图解
-
背包问题主要是指一个给定容量的背包、若干具有一定价值和重量的物品,如何选择物品放入背包使物品的价值最大。其中又分 01 背包和 完全背包(完全背包指的是:每种物品都有无限件可用)
-
这里的问题属于 01 背包,即每个物品最多放一个。而无限背包可以转化为 01 背包。
-
算法的主要思想,利用动态规划来解决。每次遍历到的第 i 个物品,根据 w[i]和 v[i]来确定是否需要将该物品放入背包中。即对于给定的 n 个物品,设 v[i]、w[i]分别为第 i 个物品的价值和重量,C 为背包的容量。再令 v[i][j]表示在前 i 个物品中能够装入容量为 j 的背包中的最大价值。则我们有下面的结果:
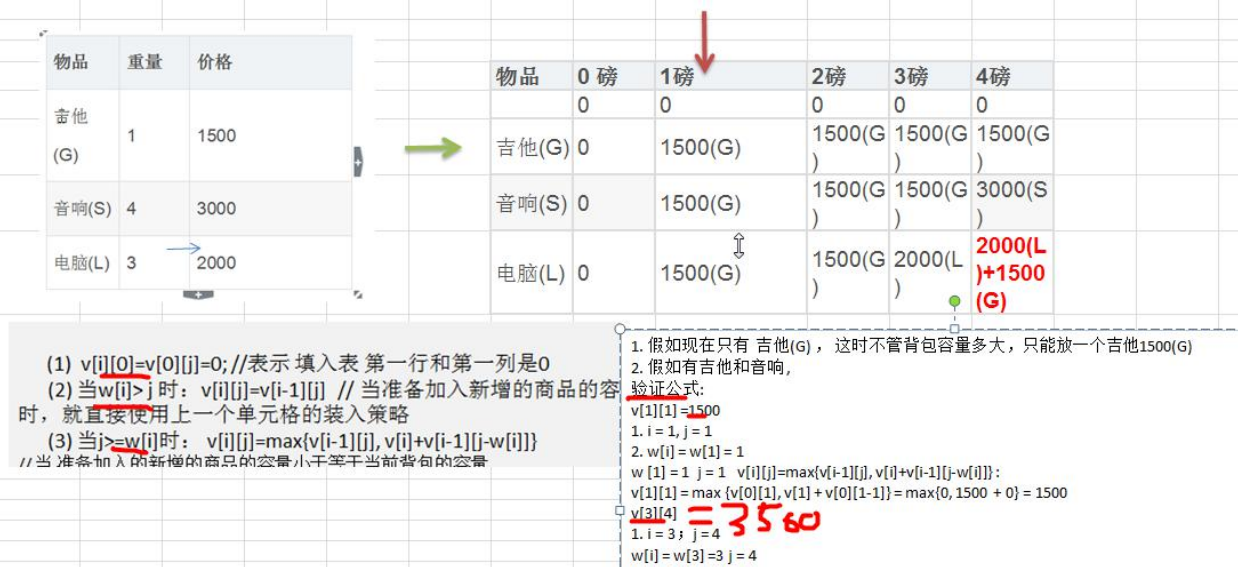
(1) v[i][0]=v[0][j]=0; //表示 填入表 第一行和第一列是 0
(2) 当 w[i]> j 时:v[i][j]=v[i-1][j] // 当准备加入新增的商品的容量大于 当前背包的容量时,就直接使用上一个单元格的装入策略
(3) 当 j>=w[i]时: v[i][j]=max{v[i-1][j], v[i]+v[i-1][j-w[i]]}
// 当 准备加入的新增的商品的容量小于等于当前背包的容量,
// 装入的方式:
v[i-1][j]: 就是上一个单元格的装入的最大值
v[i] : 表示当前商品的价值
v[i-1][j-w[i]] : 装入 i-1 商品,到剩余空间 j-w[i]的最大值
当 j>=w[i]时: v[i][j]=max{v[i-1][j], v[i]+v[i-1][j-w[i]]} :
- 图解的分析
![]()
4.动态规划-背包问题的代码实现
- 代码实现(韩老师)
public class KnapsackProblem {
public static void main(String[] args) {
// TODOAuto-generated method stub
int[] w = {1, 4, 3};//物品的重量
int[] val = {1500, 3000, 2000}; //物品的价值 这里 val[i] 就是前面讲的 v[i]
int m = 4; //背包的容量
int n = val.length; //物品的个数
//创建二维数组,
//v[i][j] 表示在前 i 个物品中能够装入容量为 j 的背包中的最大价值
int[][] v = new int[n+1][m+1];
//为了记录放入商品的情况,我们定一个二维数组
int[][] path = new int[n+1][m+1];
//初始化第一行和第一列, 这里在本程序中,可以不去处理,因为默认就是 0
for(int i = 0; i < v.length; i++) {
v[i][0] = 0; //将第一列设置为 0
}
for(int i=0; i < v[0].length; i++) {
v[0][i] = 0; //将第一行设置 0
}
//根据前面得到公式来动态规划处理
for(int i = 1; i < v.length; i++) { //不处理第一行 i 是从 1 开始的
for(int j=1; j < v[0].length; j++) {//不处理第一列, j 是从 1 开始的
//公式
if(w[i-1]> j) { // 因为我们程序 i 是从 1 开始的,因此原来公式中的 w[i] 修改成 w[i-1]
v[i][j]=v[i-1][j];
} else {
//说明:
//因为我们的 i 从 1 开始的, 因此公式需要调整成
//v[i][j]=Math.max(v[i-1][j], val[i-1]+v[i-1][j-w[i-1]]);
//v[i][j] = Math.max(v[i - 1][j], val[i - 1] + v[i - 1][j - w[i - 1]]);
//为了记录商品存放到背包的情况,我们不能直接的使用上面的公式,需要使用 if-else 来体现公式
if(v[i - 1][j] < val[i - 1] + v[i - 1][j - w[i - 1]]) {
v[i][j] = val[i - 1] + v[i - 1][j - w[i - 1]];
//把当前的情况记录到 path
path[i][j] = 1;
} else {
v[i][j] = v[i - 1][j];
}
}
}
}
//输出一下 v 看看目前的情况
for(int i =0; i < v.length;i++) {
for(int j = 0; j < v[i].length;j++) {
System.out.print(v[i][j] + " ");
}
System.out.println();
}
System.out.println("============================");
//输出最后我们是放入的哪些商品
//遍历 path, 这样输出会把所有的放入情况都得到, 其实我们只需要最后的放入
// for(int i = 0; i < path.length; i++) {
// for(int j=0; j < path[i].length; j++) {
// if(path[i][j] == 1) {
// System.out.printf("第%d 个商品放入到背包\n", i);
// }
// }
// }
//动脑筋
int i = path.length - 1; //行的最大下标
int j = path[0].length - 1; //列的最大下标
while(i > 0 && j > 0 ) { //从 path 的最后开始找
if(path[i][j] == 1) {
System.out.printf("第%d 个商品放入到背包\n", i);
j -= w[i-1]; //w[i-1]
}
i--;
}
}
}
- 代码实现(自己)
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
/**
* 动态规划-背包问题的代码实现
*/
public class KnapsackProblem {
public static void main(String[] args) {
Product[] products = new Product[3];
products[0] = new Product("G", 1, 1500);
products[1] = new Product("S", 4, 3000);
products[2] = new Product("L", 3, 2000);
//物品的重量
//int[] w = {1, 4, 3};
//物品的价值 这里 val[i] 就是前面讲的 v[i]
//int[] val = {1500, 3000, 2000};
//物品的个数
int n = products.length;
//背包的容量
int m = 4;
//创建二维数组,
//v[i][j] 表示在前 i 个物品中能够装入容量为 j 的背包中的最大价值
int[][] v = new int[n + 1][m + 1];
List<Product>[][] lists = new ArrayList[n + 1][m + 1];
//初始化第一行和第一列, 这里在本程序中,可以不去处理,因为默认就是 0
for (int i = 0; i < v.length; i++) {
v[i][0] = 0; //将第一列设置为 0
}
for (int i = 0; i < v[0].length; i++) {
v[0][i] = 0; //将第一行设置 0
}
//根据前面得到公式来动态规划处理
for (int i = 1; i < v.length; i++) { //不处理第一行 i 是从 1 开始的
for (int j = 1; j < v[i].length; j++) {//不处理第一列, j 是从 1 开始的
//公式
if (products[i - 1].weight > j) { // 因为我们程序 i 是从 1 开始的,因此原来公式中的 w[i] 修改成 w[i-1]
v[i][j] = v[i - 1][j];
lists[i][j] = lists[i - 1][j];
} else {
//说明:
//因为我们的 i 从 1 开始的, 因此公式需要调整成
int pre_v = v[i - 1][j];
int cur_v = products[i - 1].value + v[i - 1][j - products[i - 1].weight];
List<Product> productListPre = lists[i - 1][j - products[i - 1].weight];
if (cur_v > pre_v) {
v[i][j] = cur_v;
if (lists[i][j] == null) {
lists[i][j] = new ArrayList<>();
}
if (productListPre != null) {
lists[i][j].addAll(productListPre);
}
lists[i][j].add(products[i - 1]);
} else {
v[i][j] = pre_v;
lists[i][j] = productListPre;
}
}
}
}
//遍历
for (int i = 0; i < v.length; i++) {
for (int j = 0; j < v[i].length; j++) {
System.out.print(v[i][j] + "\t");
}
System.out.println();
}
System.out.println("==========");
//遍历
for (int i = 0; i < lists.length; i++) {
for (int j = 0; j < lists[i].length; j++) {
System.out.print(lists[i][j] + "\t");
}
System.out.println();
}
System.out.println("==========");
List<Sum> sumList = showResult(lists);
Collections.sort(sumList);
System.out.println(sumList);
}
public static List<Sum> showResult(List<Product>[][] lists) {
List<Sum> sumList = new ArrayList<>();
for (int i = 0; i < lists.length; i++) {
for (int j = 0; j < lists[i].length; j++) {
if (lists[i][j] != null) {
int sum = 0;
for (int k = 0; k < lists[i][j].size(); k++) {
sum += lists[i][j].get(k).value;
}
sumList.add(new Sum(sum, lists[i][j]));
}
}
}
return sumList;
}
static class Sum implements Comparable<Sum> {
public int sum;
public List<Product> products;
public Sum(int sum, List<Product> products) {
this.sum = sum;
this.products = products;
}
@Override
public int compareTo(Sum o) {
return o.sum - sum;
}
@Override
public String toString() {
return "Sum{" +
"sum=" + sum +
", products=" + products +
'}';
}
}
static class Product {
public String name;
public int weight;
public int value;
public Product(String name, int weight, int value) {
this.name = name;
this.weight = weight;
this.value = value;
}
@Override
public String toString() {
return "Product{" +
"name='" + name + '\'' +
", weight=" + weight +
", value=" + value +
'}';
}
}
}
- 输出结果
0 0 0 0 0
0 1500 1500 1500 1500
0 1500 1500 1500 3000
0 1500 1500 2000 3500
==========
null null null null null
null [Product{name='G', weight=1, value=1500}] [Product{name='G', weight=1, value=1500}] [Product{name='G', weight=1, value=1500}] [Product{name='G', weight=1, value=1500}]
null [Product{name='G', weight=1, value=1500}] [Product{name='G', weight=1, value=1500}] [Product{name='G', weight=1, value=1500}] [Product{name='S', weight=4, value=3000}]
null [Product{name='G', weight=1, value=1500}] [Product{name='G', weight=1, value=1500}] [Product{name='L', weight=3, value=2000}] [Product{name='G', weight=1, value=1500}, Product{name='L', weight=3, value=2000}]
==========
[Sum{sum=3500, products=[Product{name='G', weight=1, value=1500}, Product{name='L', weight=3, value=2000}]}, Sum{sum=3000, products=[Product{name='S', weight=4, value=3000}]}, Sum{sum=2000, products=[Product{name='L', weight=3, value=2000}]}, Sum{sum=1500, products=[Product{name='G', weight=1, value=1500}]}, Sum{sum=1500, products=[Product{name='G', weight=1, value=1500}]}, Sum{sum=1500, products=[Product{name='G', weight=1, value=1500}]}, Sum{sum=1500, products=[Product{name='G', weight=1, value=1500}]}, Sum{sum=1500, products=[Product{name='G', weight=1, value=1500}]}, Sum{sum=1500, products=[Product{name='G', weight=1, value=1500}]}, Sum{sum=1500, products=[Product{name='G', weight=1, value=1500}]}, Sum{sum=1500, products=[Product{name='G', weight=1, value=1500}]}, Sum{sum=1500, products=[Product{name='G', weight=1, value=1500}]}]



 浙公网安备 33010602011771号
浙公网安备 33010602011771号