1.为什么要有图
- 前面我们学了线性表和树
- 线性表局限于一个直接前驱和一个直接后继的关系
- 树也只能有一个直接前驱也就是父节点
- 当我们需要 表示多对多的关系时, 这里我们就用到了图
2.图的举例说明
图是一种数据结构,其中结点可以具有零个或多个相邻元素。两个结点之间的连接称为边。 结点也可以称为顶点。如图:

3. 图的常用概念
-
顶点(vertex)
-
边(edge)
-
路径
-
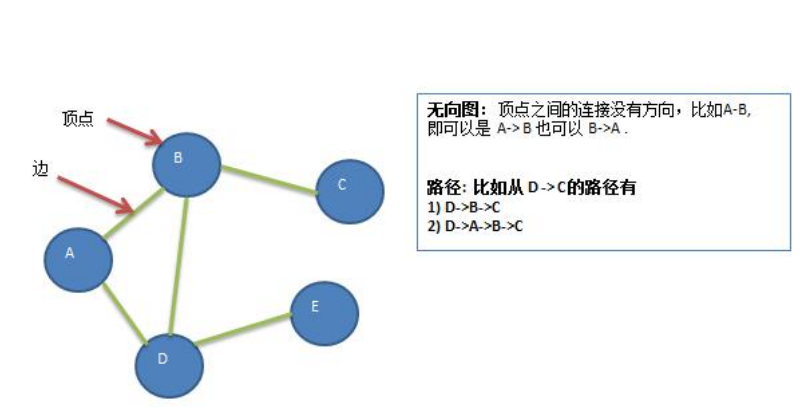
无向图(右图
![]()
-
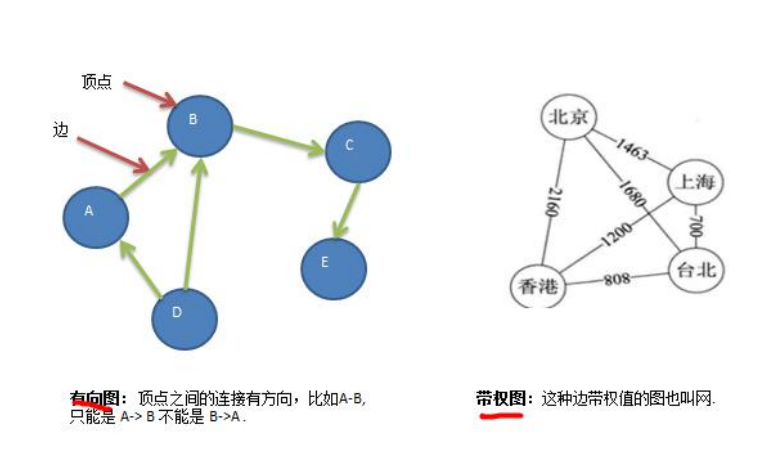
有向图
-
带权图
![]()
4.图的表示方式
图的表示方式有两种:二维数组表示(邻接矩阵);链表表示(邻接表)。
4.1.邻接矩阵
邻接矩阵是表示图形中顶点之间相邻关系的矩阵,对于 n 个顶点的图而言,矩阵是的 row 和 col 表示的是 1....n个点。
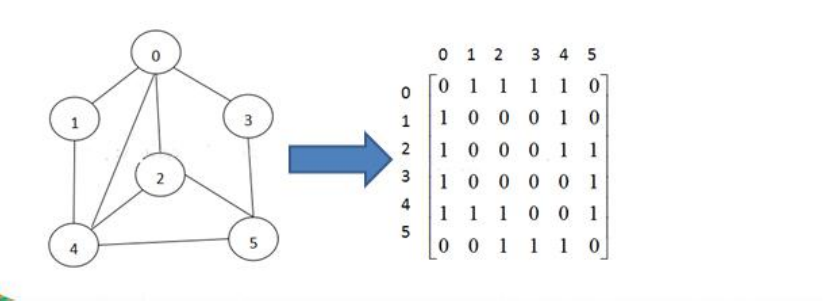
4.2.邻接表
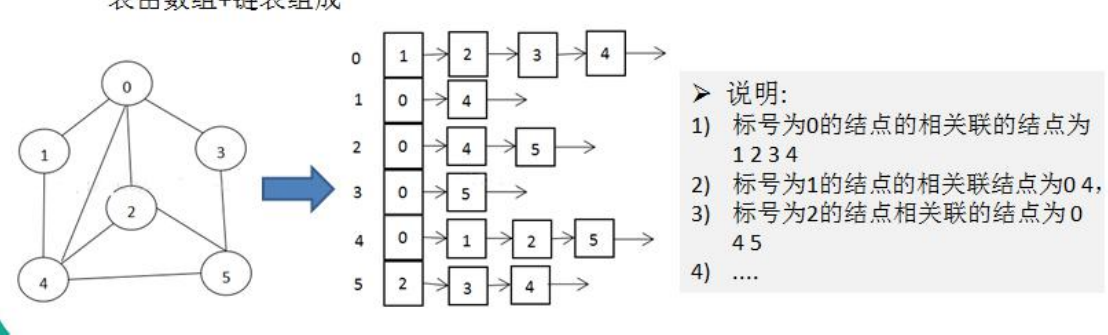
- 邻接矩阵需要为每个顶点都分配 n 个边的空间,其实有很多边都是不存在,会造成空间的一定损失.
- 邻接表的实现只关心存在的边,不关心不存在的边。因此没有空间浪费,邻接表由数组+链表组成
- 举例说明
![]()
5.图的快速入门案例
-
要求: 代码实现如下图结构
![]()
-
思路分析 (1) 存储顶点 String 使用 ArrayList (2) 保存矩阵 int[][] edges
-
代码实现
//核心代码,汇总在后面
//插入结点
public void insertVertex(String vertex) {
vertexList.add(vertex);
}
//添加边
/**
*
* @param v1 表示点的下标即使第几个顶点 "A"-"B" "A"->0 "B"->1
* @param v2 第二个顶点对应的下标
* @param weight 表示
*/
public void insertEdge(int v1, int v2, int weight) {
edges[v1][v2] = weight;
edges[v2][v1] = weight;
numOfEdges++;
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号