原码、反码、补码的产生、应用以及优缺点有哪些？

第一篇：(受益匪浅)

原码：将一个整数，转换成二进制，就是其原码。
如单字节的5的原码为：0000 0101；-5的原码为1000 0101。

　反码：正数的反码就是其原码；负数的反码是将原码中，除符号位以外，每一位取反。
如单字节的5的反码为：0000 0101；-5的反码为1111 1010。

　补码：正数的补码就是其原码；负数的反码+1就是补码。
如单字节的5的补码为：0000 0101；-5的补码为1111 1011。

　　在计算机中，正数是直接用原码表示的，如单字节5，在计算机中就表示为：0000 0101。
负数用补码表示，如单字节-5，在计算机中表示为1111 1011。

这儿就有一个问题，为什么在计算机中，负数用补码表示呢？为什么不直接用原码表示？如单字节-5：1000 0101。
　　
我想从软件上考虑，原因有两个

　1、表示范围
　　拿单字节整数来说，无符号型，其表示范围是[0,255]，总共表示了256个数据。有符号型，其表示范围是[-128,127]。
　　先看无符号，0表示为0000 0000，255表示为1111 1111，刚好满足了要求，可以表示256个数据。
　　再看有符号的，若是用原码表示，0表示为0000 000。因为咱们有符号，所以应该也有个负0（虽然它还是0）：1000 0000。

　　那我们看看这样还能够满足我们的要求，表示256个数据么？
　　正数，没问题，127是0111 1111，1是0000 0001，当然其它的应该也没有问题。
　　负数呢，-1是1000 0001，那么把负号去掉，最大的数是111 1111，也就是127，所以负数中最小能表示的数据是-127。
　　这样似乎不太对劲，该如何去表示-128？貌似直接用原码无法表示，而我们却有两个0。
　　如果我们把其中的一个0指定为-128，不行么？这也是一个想法，不过有两个问题：一是它与-127的跨度过大；二是在用硬件进行运算时不方便。
　　所以，计算机中，负数是采用补码表示。
如 单字节-1，原码为1000 0001，反码为1111 1110，补码为1111 1111，计算机中的单字节-1就表示为1111 1111。

　　单字节-127，原码是1111 1111，反码1000 0000，补码是1000 0001，计算机中单字节-127表示为1000 0001。
　　
单字节-128，原码貌似表示不出来，除了符号为，最大的数只能是127了，其在计算机中的表示为1000 0000。

　　2、大小的习惯（个人观点）
　　也可以从数据大小上来理解。还是以单字节数据为例。有符号数中，正数的范围是[1,127]，最大的是127，不考虑符号为，其表示为111 1111；最小的是1，不考虑符号为，其表示为000 0001。
　　负数中，最大的是-1，我们就用111 1111表示其数值部分。后面的数据依次减1。减到000 0001的时候，我们用它标示了-127。再减去1，就变成000 0000了。还好我们有符号位，所以有两个0。把其中带符号的0拿过来，表示-128，刚好可以满足表示范围[由此可见-128实际上就是-0]。

计算机中的1000 0000可以表示无符号的128，也可以表示有符号的-128(-0).

　 以上只是从软件的角度进行了分析，当然，从硬件的角度出发，负数使用补码表示也是有其原因的，毕竟计算机中，最终实现运算的还是硬件。
主要原因有三
　　1>、负数的补码，与其对应正数的补码之间的转换可以用同一种方法----求补运算完成，简化硬件。
　　如[注:无论正数还是负数,将其在计算机中存储的方式视为原码]

From	To	原码	反码[所有位取反]	补码
-127	127	1000 0001	0111 1110	0111 1111
127	-127	0111 1111	1000 0000	1000 0001
-128	128	1000 0000	0111 1111	1000 0000
128	-128	1000 0000	0111 1111	1000 0000

　　可以发现，负数和正数求补的方法是一样的。

　　2>、可以将减法变为加法，省去了减法器。
　　在计算机中，我们可以看到，对其求补，得到的结果是其数值对应的负数。同样，负数也是如此。
　　运算中，减去一个数，等于加上它的相反数，这个小学就学过了。既然其补码就是其相反数，我们加上其补码不就可以了。
　　如：A - 127，
　　也就相当于：A + (-127)，
　　又因为负数是以补码的形式保存的，也就是负数的真值是补码，既然这样，当我们要减一个数时，直接把其补码拿过来，加一下，就OK了，我们也可以放心地跟减法说拜拜了！
　　当然这也涉及到类型转换的问题，如单字节128，其原码是1000 0000，其补码也是1000 0000。这样我们+128，或者-128，都是拿1000 0000 过来相加，这样不混乱掉了？还好，各个编程语言的编辑器对有类型转换相关的限制。
　　如：（假设常量都是单字节）
+ 128， 真值的运算是 0000 0001 + 1000 0000 ，如果你将结果赋值给一个单字节有符号正数，编辑器会提示你超出了表示范围。因为运算的两个数据是无符号的，其结果也是无符号的129，而有符号单字节变量最大可以表示的是127。
- 128，真值的运算是 0000 0001 + 1000 0000 ，因为-128是有符号，其运算结果也是有符号，1000 0001，刚好是-127在计算机中的真值。

　　3>、无符号及带符号的加法运算可以用同一电路完成。
　　有符号和无符号的加减，其实都是把它们的真值拿过来相加。真值，也就是一个数值在计算机中的二进制表示。正数的真值就是其原码，负数的真值是其补码。所以，有符号和无符号由编译器控制，计算机要做的不过是把两个真值拿过来相加。

---

---

---

---

第二篇

作者：张天行
链接：https://www.zhihu.com/question/20159860/answer/119405396
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

二、重温运算规则

首先我想把整套关于原码反码补码的运算规则准确清晰地写一遍，方便急需应用的知友参考，也希望大家首先能记住这套规定，再开始进一步的探讨。

所谓原码就是机器数，是加了一位符号位的二进制数，正数符号位为0，负数符号位为1，计算机中存储、处理、运算的数据通常是8位、16位、32位或64位的，这里以最简单的8位为例讲解。注意符号位是包含在8位中的其中1位，故可直观读出的数只有7位（只有后7位数可以按权展开）。有心人可能注意到原码是有缺陷的，它只能表示255种状态，因为00000000（＋0）和10000000（－0）其实是一个数，因此原码的表示范围成了－127到＋127，这个问题需要神奇的补码来解决，因为在补码中10000000被用来表示－128。

【自注： +0 ，-0原码和反码都各自有一个，但是两者的补码都一样，都是 0000 0000 】

所谓反码，英语里又叫ones' complement（对1求补），这里的1，本质上是一个有限位计数系统里所能表示出的最大值，在8位二进制里就是11111111，在1位十进制里就是9，在3位十六进制里就是FFF（再大就要进位了）。求反又被称为对一求补，用最大数减去一个数就能得到它的反，很容易看出在二进制里11111111减去任何数结果都是把这个数按位取反，0变1，1变零，所以才称之为反码。用原码求反码的方法是，正数不变，负数保留符号位1不变，剩下位按位取反。

所谓补码，英语里又叫two's complement（对2求补），这个2指的是计数系统的容量（模），就是计数系统所能表示的状态数。对1位二进制数来说只有0和1两种状态，所以模是10也就是十进制的2，对7位二进制数来说就是10000000，这个模是不可能取到的，因为位数多一位。用模减去一个数（无符号部分）就能得到这个数的补，比如10000000－1010010=0101110，事实上因为10000000=1111111+1，稍加改变就成了（1111111－1010010）+1，所以又可以表述为先求反再加1。总结求补码的方法就是正数依旧不变，负数保留符号位不变，先求反码再加上1。

记住了怎么求补码，接下来讲讲运算。通过原码的符号位和数值，我们能迅速指出它代表的数，判断其正负并进行四则运算，相比而言反码和补码对于人则显得过于晦涩。如果说原码是给人看的数字语言，那么补码就是计算机的数字语言。计算机不需要知道什么是正负、大小，这些判断对它而言过于复杂。事实上它存储、处理、传输的数都只有补码一种形式，人所做的加减乘除，在计算机里只通过相加和移位就能解决，这都来自于补码系统的内在自洽和巧夺天工的神奇魔力，也是后文要阐述的重点。

对加法和减法，按上文的方法求得补码之后，直接相加就可以了，但相加的时候符号位一定要一起参与运算，有时候，两符号位相加或者接受来自低位的进位会发生溢出，就扔掉溢出的一位（稍后会解释为什么），由新的符号位决定结果的正负，如果是0表示正数，结果就是原码，如果是1表示负数，结果还要再求补数得到原码（   补码再补码就是原码，即原码和补码互为补码，两者互换的方法都有两种[对负数来讲]，①符号位不变，其他位取反再加1；②符号位不变，先减 1然后其他位取反，  ）。

至此我介绍了原码反码补码的规定，以及如何求补码并进行加减法（乘除暂不涉及，事实上懂了加减法的奥秘，乘除很容易理解），对于一个工程人才来说，上面的内容已经足够应付所有具体问题。剩下的则是一些“无用”的思考，关于为何这套法则能够化减为加，以及人为规定的符号位在运算中为何总是能精确地指示结果的符号。

三、无用之用

数字是用来记录现实世界数量属性的语言。

而任何计数系统都必须有两个参数：容量和精度。

模是衡量计数系统容量的参数。模代表了计数系统所能表示和存储的状态数。

任何有限的计数系统都有一个确定的模。如时钟的模是12（即只有一个位的十二进制系统，若再加一个大钟，使小钟转一周大钟加一刻度，就是有两个位的十二进制系统），再比如8位计算机的模是2^8=256D（每一位也可以单独看做一个模为2的计数系统）。

问题一：化减为加

对同一计数系统中的数量可以定义运算如加减，但运算结果超出预设位数时，就要发生溢出，这个溢出其实就是模，是时钟的一整圈（因此丢掉它没有影响），如果进位没有被另一个计数系统接受，结果看似“失真”，本质上是进入了“第二次循环”。
以时钟系统为例：8+7=15D=13（十二进制）>10（十二进制），进位1溢出丢失（除非用另一个时钟接收这个进位），在表盘上（即一位十二进制计数系统中）呈现为3，而8-5=8+(-5)=3也得到了相同结果。这就说明在有限容量的计数系统中，+7和-5是完全相同的，而它们正是关于模12的一对补数。

因此我们在有限的计数系统做了这种定义：正数补数即为本身，负数A【补】=模-绝对值（A）。一个数加上另一个数（可以是正数也可以是负数），结果等于加上这个数的补数，若有进位则舍弃进位。这么做的重大意义在于极大地方便了计算机进行数据处理，要知道对人而言减法并非难事，但用门电路实现就复杂得多了，减之前还要判断大小考虑次序。

问题二：符号位参与运算

在8位计算机中，一个字节可以表示256种状态，把字节看做一个钟的话，刻度可以随便标，不如取0点钟为-128，正对的6点钟为0，即存储范围是从-128到127，用二进制补码表示是10000000~01111111（10000000用来表示-128似乎是人为定义的，因为原码无法表示-128，按正常程序更无法求得其补码）。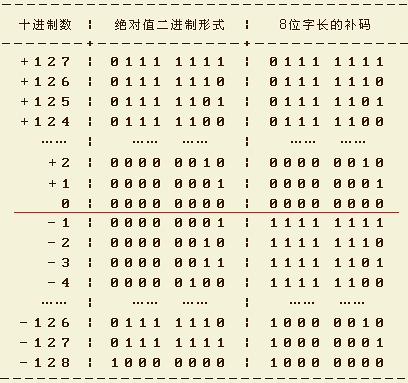

符号位是我认为理解补码的关键所在，也是关于补码最神奇的地方。人类“生硬”地添加了符号位，把256种状态剪成正负两半，还“生硬”地规定-128的补码为10000000，但用补码运算的时候，一切就像“水往低处流”般正确和谐自然：符号位参与运算，接受来自低位的进位，永远能忠实地指示结果的正负。

我举个例子，你们感受一下：

所谓的“负数加负数会变成正数，正数加正数会变成负数”，本质还是在于，计数系统是无法表示超出其取值范围的计算结果的。

120D+120D=01111000B+01111000B=11110000B，符号位的1来自低位进位，指示了结果是负数，所以需要求补得10010000B也就是-16D，放在钟面上就是从120顺时针旋转120格到240的位置，只不过系统最大只取到127，240的位置就是-16的位置，而且-16和240正是关于模256的一对补数。-120D-120D=16D也是一样的道理。在有限的计数系统内，由于位数的限制，发生溢出的情况下无法得到计算真实值，得到的是真实值关于模的补数。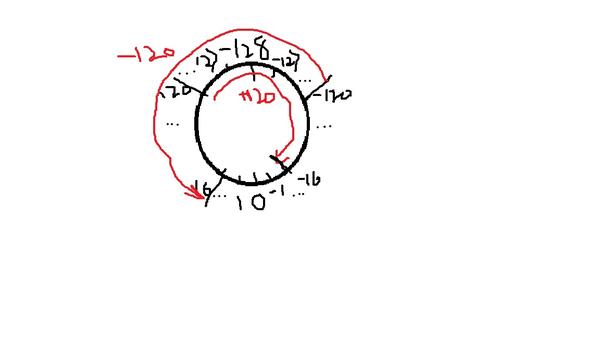

看到这里是不是有那么点味道呢，我给你们总结一下：加法都是从低位往高位做的，如果两个数（补码），后七位相加产生了进位，说明
又溢出了一次，每当溢出一次（就是越过了-128这个正负分界点），符号就要反一下，0变1，1变0。符号是1的，说明大得越界了，需要再求个补，用取值范围内的负数表示结果；符号是0的，说明小得越界了，但由于正数的补数就是本身，就不必再求补了。

四、后记

从八月底的初稿到这篇文章，中间经历了差不多四个月的时间，我对于补码问题的认识也经历了困惑到清晰到困惑到再清晰这一过程，其中修改超过十次，思考所花的时间更是不计其数。从参加考试的角度看，我熟记的运算规则早已足够我应付所有题目，但我仍然不愿意半途而废，原因有二：

大一学习线性代数时，曾经挂过科，因为对于定理和公式背后的含义一无所知，而老师也不加讲解，只一味让我们死记做题。虽然很多同学都适应这种所谓的“工科数学学习”，然而这对我而言简直如同梦魇，没有理解内化如何能称得上学习，不过是应付考试然后忘的精光罢了。我很幸运的是，在准备补考时读到了网上广为流传的孟岩老师的文章《理解矩阵》，我记得那是一个冬天的晚上，读完文章后我很兴奋，一直到半夜都睡不着，这是我第一次体会到数学体系的和谐自洽以及数学的深刻性在工程中的巨大威力，从那以后我才逐渐找到了学习数学的乐趣。

《理解矩阵》中有一段话至今我还记得，现摘抄如下：
自从1930年代法国布尔巴基学派兴起以来，数学的公理化、系统性描述已经获得巨大的成功，这使得我们接受的数学教育在严谨性上大大提高。然而数学公理化的一个备受争议的副作用，就是一般数学教育中直觉性的丧失。数学家们似乎认为直觉性与抽象性是矛盾的，因此毫不犹豫地牺牲掉前者。然而包括我本人在内的很多人都对此表示怀疑，我们不认为直觉性与抽象性一定相互矛盾，特别是在数学教育中和数学教材中，帮助学生建立直觉，有助于它们理解那些抽象的概念，进而理解数学的本质。反之，如果一味注重形式上的严格性，学生就好像被迫进行钻火圈表演的小白鼠一样，变成枯燥的规则的奴隶。

“枯燥的规则的奴隶”又何止是在数学教学中出现的呢？如果你在大学工科学习过，你会发现这些人简直遍地都是，拿我在的浙大为例，有的是学生对课程并不理解，单靠考前突击刷题就拿到90分以上的成绩。

正是在这样的情形下，我决定尽我所能重新思考学到的每一个重要知识，并将其中一部分写成文章，一来有助于对思维的梳理，二来也是便于自己将来的回顾，倘若拙作还能对他人也有所帮助，从而使我给世界留下一些微不足道的影响，那真是幸甚了。