二叉搜索树基本操作实现
二叉搜索树又称为二叉排序树,首先二叉搜索树是一棵二叉树,所谓二叉树,就是"任意节点最多允许两个子节点",这两个子节点称为左右子节点。
二叉搜索树的性质:
1、若左子树不空,则左子树上的所有节点的值均小于其根节点的值;
2、若右子树不空,则右子树上的所有节点的值均大于其根节点的值;
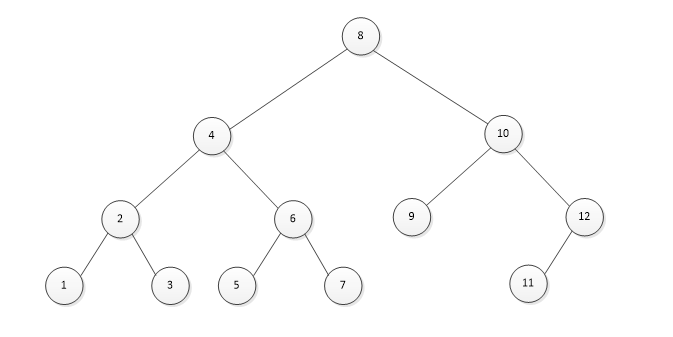
上图便是一个二叉搜索树,也就是说:任意节点的键值一定大于其左子树中的每一个节点的键值,并小于其右子树中的每一个节点的键值。
下面是自己对二叉搜索树的代码实现:
#include <iostream> using namespace std; struct TreeNode { int val; TreeNode* left; TreeNode* right; TreeNode(int x) : val(x), left(NULL), right(NULL) {}; }; TreeNode* searchBST(TreeNode* root, int key) { while (root != NULL) { if (key == root->val) return root; root = root->val > key ? root->left : root->right; } return NULL; } void insertBST(TreeNode* &root, int data) { TreeNode* node = new TreeNode(data); if (root == NULL) { root = node; return; } if (searchBST(root, data) != NULL) return; TreeNode* preNode = NULL; TreeNode* curNode = root; while (curNode) { preNode = curNode; curNode = curNode->val > data ? curNode->left : curNode->right; } if (preNode->val > data) preNode->left = node; else preNode->right = node; } void minOrderVisit(TreeNode* root) { if (root == NULL) return; minOrderVisit(root->left); cout << root->val << " "; minOrderVisit(root->right); } void deleteBST(TreeNode* &root, int data) { if (root == NULL) return; if (root->val == data) { TreeNode* p = root; if (root->left == NULL && root->right == NULL) { root = NULL; }else if (root->left == NULL) root = root->right; else if (root->right == NULL) root = root->left; else { TreeNode* temp = root->right; TreeNode* find = NULL; while (temp) { find = temp; temp = temp->left; } find->left = root->left; root = root->right; } delete p; } else if (root->val > data) deleteBST(root->left, data); else deleteBST(root->right, data); } int main() { int a[] = { 2, 1, 4, 3, 5, 6, 8, 7, 9, 10 }; int len = sizeof(a) / sizeof(a[0]); TreeNode* p = NULL; for (int i = 0; i < len; i++) { insertBST(p, a[i]); } deleteBST(p, 7); minOrderVisit(p); system("pause"); return 0; }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号