SGI STL泛型heap算法分析
heap性质
heap本质是用一个数组表示的完全二叉树,并且父节点总是大于(或者小于)子节点的值。在STL中用于实现优先队列(priority_queque)。堆排序是排序算法中是稳定效率最高的一种。STL以可以动态扩容的vector作为heap的底层数组。
push_heap分析
为满足完全二叉树的条件,新加入元素一定要放在最下一层作为叶子节点,并填补由左至右的第一个空格,也就是把新元素插入到底层vector的end()处。下图是push_heap算法的实际示意图:
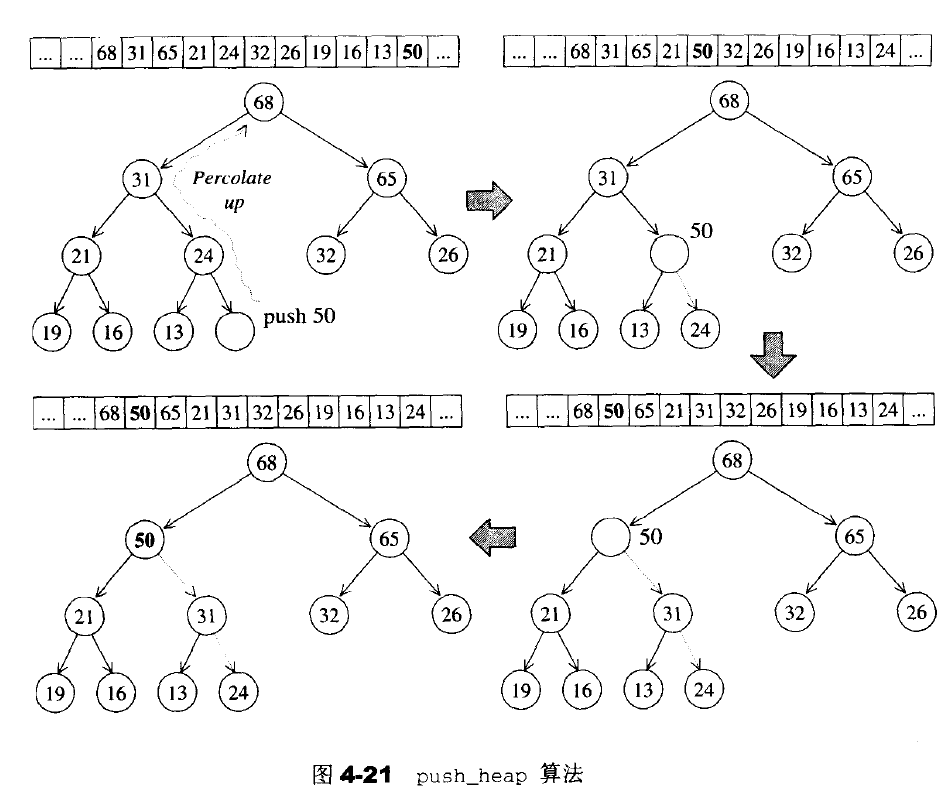
从图中可以看出push_heap算法的过程是将新加入堆的值(50),层层上挪,直到正确的位置。下面是该过程的源码:
template <class RandomAccessIterator, class Distance, class T> void __push_heap(RandomAccessIterator first, Distance holeIndex, Distance topIndex, T value) { Distance parent = (holeIndex - 1) / 2; //找出父节点 while (holeIndex > topIndex && *(first + parent) < value) { //尚未到达顶端且父节点小于洞值,使用operator<,知max-heap *(first + holeIndex) = *(first + parent); //令洞值为父值 holeIndex = parent; //新洞为父节点 parent = (holeIndex - 1) / 2; //新洞的父节点 } *(first + holeIndex) = value; //令洞值为新值 } template <class RandomAccessIterator, class Distance, class T> inline void __push_heap_aux(RandomAccessIterator first, RandomAccessIterator last, Distance*, T*) { __push_heap(first, Distance((last - first) - 1), Distance(0), T(*(last - 1))); //(last-first)–1代表新元素的索引,0是堆首的索引,*(last - 1)是新加入的值 } template <class RandomAccessIterator> inline void push_heap(RandomAccessIterator first, RandomAccessIterator last) { //注意,调用该函数时候,新元素位于最后一个位置(last-1) __push_heap_aux(first, last, distance_type(first), value_type(first)); }
push_heap的用法是输入迭代器对,并且保证[first,last-1)是最大堆,*(last-1)是新加入的元素。push_heap调用辅助函数__push_heap_aux。至于为什么需要这个辅助函数了?应该是为了提取出distance_type和value_type吧,这两个内联函数的定义,可以参考stl源码剖析迭代器的那章。下面来思考真正的实现函数__push_heap。这个函数需要新加入元素位置holeIndex和堆首位置topIndex,另外还有保存好的新加入值。算法的过程很简单,就是上溯holeIndex,找到真正满足条件的位置(无法继续上回溯),然后把value放入该位置即可。
pop_heap分析
pop_heap操作取走根节点,其实是移至底部容器vector的最后一个节点处并保存该节点。而此时需要维护vector.size()-1大小堆,需要为保存的节点在堆中找一个适当的位置。这个过程和上面的__push_heap的过程恰好相反,从根节点(此时为洞节点),层层下放,直到叶子节点位置,然后在这个位置调用push_heap加入刚刚保存的新值。下面是pop_heap算法实际示意图:
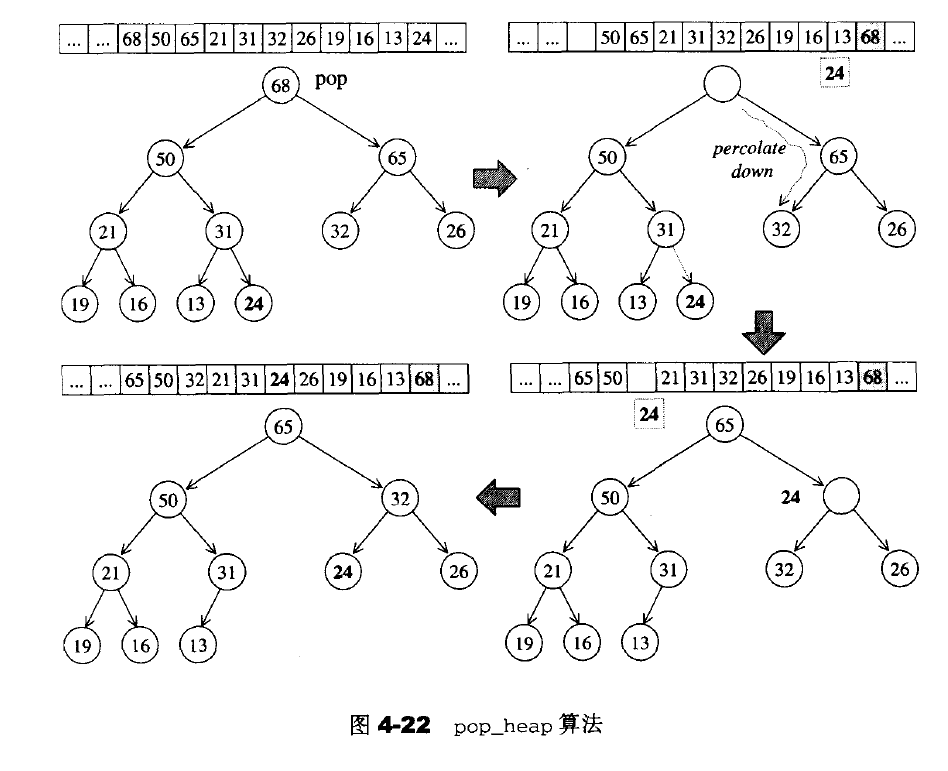
下面看pop_heap的源码:
template <class RandomAccessIterator, class Distance, class T> void __adjust_heap(RandomAccessIterator first, Distance holeIndex, Distance len, T value) { Distance topIndex = holeIndex; Distance secondChild = 2 * holeIndex + 2; //洞节点的右子节点 while (secondChild < len) { if (*(first + secondChild) < *(first + (secondChild - 1))) //左节点值大于右节点值 secondChild--; //洞节点往左下放 *(first + holeIndex) = *(first + secondChild); //洞节点下放 holeIndex = secondChild; //新洞节点 secondChild = 2 * (secondChild + 1); //新洞节点的右子节点 } if (secondChild == len) { //如果只有左子节点,洞节点下放到左子节点 *(first + holeIndex) = *(first + (secondChild - 1)); holeIndex = secondChild - 1; } __push_heap(first, holeIndex, topIndex, value); //原尾值插入到新数组中,上溯 } template <class RandomAccessIterator, class T, class Distance> inline void __pop_heap(RandomAccessIterator first, RandomAccessIterator last, RandomAccessIterator result, T value, Distance*) { *result = *first; //设定尾值为首值,于是尾值即是结果, //可由调用底层容器之 pop_back() 取出尾值 __adjust_heap(first, Distance(0), Distance(last - first), value); //以上欲重新调整 heap,洞号为 0,欲调整值为value } template <class RandomAccessIterator, class T> inline void __pop_heap_aux(RandomAccessIterator first, RandomAccessIterator last, T*) { __pop_heap(first, last - 1, last - 1, T(*(last - 1)), distance_type(first)); //pop动作的结果为底层容器的第一个元素。因此,首先设定欲调整值为尾值,然后將首值调至 //尾节点(所以以上将迭代器result设为last-1)。然后重整 [first, last-1), //使之重新成一个合格的 heap } template <class RandomAccessIterator> inline void pop_heap(RandomAccessIterator first, RandomAccessIterator last) { __pop_heap_aux(first, last, value_type(first)); }
类似于push_heap,pop_heap也是调用辅助函数__pop_heap_aux。__pop_heap_aux调用__pop_heap。__pop_heap调用__adjust_heap调整holeIndex,最终在holeIndex处调用push_heap函数插入value(原最后一个的值)。关键代码是__adjust_heap中的循环。循环的主要意思是将holeIndex不断下放,直到最底层。最后的if语句的意思是,如果最底层有左子节点,而没有右子节点,那么最终位置肯定是这个左子节点。侯捷注释说,最后一句代码的意思是加入value到holeIndex,由于已经调整完毕,所以一个赋值操作也可以达到要求。这种说法其实是错误的,如果__adjust_heap只是用在pop_heap实现完全没有问题,但在下面的make_heap也用到__adjust_heap这个函数,此时一个赋值操作是完全达不到目的的。因为make_heap调整__adjust_heap调整时value和子树中的节点的值的大小是还不确定的,需要上溯加入。后面有测试验证。
make_heap分析
这个算法用来将一段现有的数据转化为一个heap,即将一个迭代器对的内容构造成最大堆。代码如下:
template <class RandomAccessIterator, class T, class Distance> void __make_heap(RandomAccessIterator first, RandomAccessIterator last, T*, Distance*) { if (last - first < 2) return; //如果长度小于2,不必排序直接退出 Distance len = last - first; //找出第一个需要重排的子树头部,以 parent 标示出。由于任何叶节点都不需执行 //perlocate down,所以有以下計算 Distance parent = (len - 2)/2; while (true) { //调整以 parent 为首的子树。len 是为了 __adjust_heap() 判断做范围 __adjust_heap(first, parent, len, T(*(first + parent))); if (parent == 0) return; //走完根节点结束 parent--; //重排子树头部退一格 } } template <class RandomAccessIterator> inline void make_heap(RandomAccessIterator first, RandomAccessIterator last) { __make_heap(first, last, value_type(first), distance_type(first)); }
__make_heap中代码的思路也很简单。从原序列的中间位置开始不断调整(调用__adjust_heap),每次调整的目的是以当前位置为根的构建一个子堆。至于为什么从中间位置开始就可以了?原因很简单,最底层元素的数目大致就会占了一半了。
sort_heap分析
sort_heap就比较简单了,不断将极值移动到末尾,不断pop_heap。代码如下:
//每执行一次 pop_heap(),极值(在STL heap中为极大值)即被放在尾端。 //扣除尾端再执行一次 pop_heap(),次极值又被放在新尾端。一直下去,最后即得排序結果。 //每执行 pop_heap() 一次,操作范围即退缩一格 template <class RandomAccessIterator> void sort_heap(RandomAccessIterator first, RandomAccessIterator last) { while (last - first > 1) pop_heap(first, last--); }
测试验证
测试代码:
void test_heap() { int ia[9] = {0, 1, 2, 3, 4, 8, 9, 3, 5}; STD::vector<int> vec(ia, ia+9); STD::make_heap(vec.begin(), vec.end()); for (auto i : vec) { std::cout << i << " "; } std::cout << std::endl; std::cout << "sort_heap:" << std::endl; STD::sort_heap(vec.begin(), vec.end()); for (auto i : vec) { std::cout << i << " "; } std::cout << std::endl; }
结果:
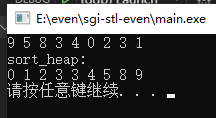
如果按照上文将的在__adjust_heap实现中用一个赋值操作代替push_heap函数,即__adjust_heap实现改为如下:
template <class RandomAccessIterator, class Distance, class T> void __adjust_heap(RandomAccessIterator first, Distance holeIndex, Distance len, T value) { Distance topIndex = holeIndex; Distance secondChild = 2 * holeIndex + 2; //洞节点的右子节点 while (secondChild < len) { if (*(first + secondChild) < *(first + (secondChild - 1))) //左节点值大于右节点值 secondChild--; //洞节点往左下放 *(first + holeIndex) = *(first + secondChild); //洞节点下放 holeIndex = secondChild; //新洞节点 secondChild = 2 * (secondChild + 1); //新洞节点的右子节点 } if (secondChild == len) { //如果只有左子节点,洞节点下放到左子节点 *(first + holeIndex) = *(first + (secondChild - 1)); holeIndex = secondChild - 1; } *(first + holeIndex) = value; // __push_heap(first, holeIndex, topIndex, value); //原尾值插入到新数组中,上溯 }
继续运行上面一开始的测试代码,结果:
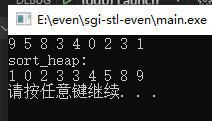
所以,侯捷的说法是错误的,遵循源码的实现才正确。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号