Pollard's Rho Algorithm 教程

[前言]

一般而言， 实现分解质因数有两种方式 :

(1). 用筛法 $O(N)$ 预处理每个数的最小质因子 ，从而在 $O(logN)$ 的时间内完成单次分解。 此算法的空间复杂度是 $O(N)$ 的。

(2). 枚举 $2$ 到 $\sqrt{N}$ 中每个数 ， 进行试除法。 此算法的时间复杂度为 $O(\sqrt{N})$ , 而空间复杂度为 $O(1)$。

可以看出这两种做法的时间复杂度开支都太大了。 而本文介绍的 Pollard's Rho Algorithm 可以在
$O(N^{\frac{1}{4}}+\frac{N^{\frac{1}{4}}*\alpha(N)}{\beta}+\beta*\alpha(N))$ ($\alpha(N)$ 表示求最大公约数的复杂度) 的时间内 ， 花费 $O(1)$ 空间完成找出给定数 $N$ 的一个非平凡因子 $p$。

[前置内容]

在理解 Pollard's Rho Algorithm 的原理之前 ， 首先我们需要了解以下知识 :

Miller-Rabin 素数测试 :

如何判断一个数是质数？ 最朴素的方法是 : 枚举 $2$ 到 $\sqrt{N}$ 中每个数 ， 判断其是否是 $N$ 的约数。 但这样的时间复杂度达到了 $O(\sqrt{N})$。 我们有更优的做法 :

首先 ， 根据费马小定理 ， 若 $p$ 是质数 ， 那么对于 $0 < a < p$ , 有 $a^{p-1}\equiv1\ (mod\ \ p)$

我们还知道若 $p$ 是质数 ， 且 $x^2\equiv1\ (mod\ \ p)$ ， 那么 $x\equiv1\ (mod\ \ p)$ 或 $x\equiv p-1\ (mod\ \ p)$ 中必有一式成立。这是因为 $x^2\equiv1\ (mod\ \ p)$ 可以推出 $(x-1)(x+1)\equiv0\ (mod\ \ p)$。

那么我们就得到了一个判定方法 : 对于要判断的数 $N$ , 选取一底数 $a$ 满足 $a < N$ , 判断引理 $1$ 或 $2$ 是否成立。 若不成立直接得到 $N$ 是合数 , 接着反复验证引理 $2$ 是否成立 (若指数 $N$ 是奇数，且 $a^{N-1}\equiv1\ (mod\ \ N)$ ， 就可以将 $N$ 变为 $\frac{N-1}{2}$)。

这样单次测试的错误率是 $\frac{1}{4}$ ，然而通过选取多个不同的底数 ， 可以将错误率降低至 $\frac{1}{4 ^ {k}}$。

具体而言 ， 对于 $N < 2^{64}$ ， 选取前十二个质数作为底数即可达到 $100\%$ 的正确率。

此算法将时间复杂度提高至最劣情况下 $O(log^2N)$ 。

生日悖论 :

我们知道， 在中国大多数高中 ， 每个班有 $40$ 到 $50$ 位同学。 你的班级是否有两个有缘人是同年同月同日生呢？ 这样的概率是很大的 ， 由下图就可以知晓。

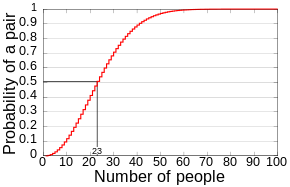
(此图来源为 Wikipedia)

事实上，我们可以用函数表示 $N$ 个人生日两两不同的概率 :

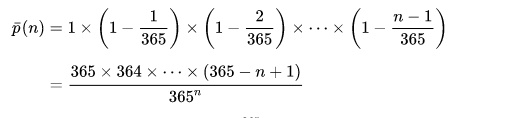
当 $N = 23$ 时 ， 存在两人生日相同的概率就达到了 $50\%$。 这也对应了上图。

弗洛伊德判环法 :

我们来解决一个这样的问题 : 有一个伪随机数列 $a$ 和随机函数 $f$ , 其递推公式为 $a_{i} = f_{a_{i - 1}}$。这个序列存在一个循环节 ， 请给出循环开始的第一个位置 $\mu$ 和环长 $\phi$。

解决这个问题最简单的方法是用平衡树 / 哈希表判断每个数是否在之前出现过了，这样的时间复杂度是 $O((\mu + \phi)log(\mu + \phi))$ 的。 并且花费了 $O(\mu + \phi)$ 的空间。而弗洛伊德的方法是 : 用两个指针，一个指针每次走一步，另一个每次走两步， 如果两个指针指向的数对应值相同 ， 那么就找到了一个或若干个循环 ， 在这个基础上可以轻松得到 $\mu$ 与 $\phi$ 的具体值。简而言之 ， 就是需要找到第一个 $i$ 满足 $a_{i} = a_{2i}$。

我们分析此做法的时间复杂度 : 对于任意 $i$ 满足 $i \geq \mu$ ，都有 $a_{i} = a_{i + k\phi}$。 由 $a_{i} = a_{2i}$ 可以推得 $i + k\phi = 2i$ , $i = k\phi$。 因此我们找到的 $i$ 事实上是第一个 $k$ 满足 $k\phi \geq \mu$。

因此此算法时间复杂度是 $O(\phi + \mu)$ 的。 并且空间复杂度只有 $O(1)$。

Richard P. Brent 教授对这个算法做了一些常数优化。 思路是 : 每次走 $2$ 的次幂步 ， 直到发现循环为止。 这个优化使我们可以直接找到 $\phi$ 的精确值。根据他本人的试验， 此做法将 Pollard's Rho Algorithm 的运行效率提高约 $24\%$。

[算法流程]

我们已经了解了上述知识 ， 下面回归问题本身 ， 如何快速分解质因数？

首先用 Miller-Rabin 素数测试判断 $N$ 是否是质数。

然后 ， 一个简单思路是 ， 若我们能找到 $N = pq$ ($p$ 和 $q$ 是 $N$ 的非平凡因子) ， 便可以将 $p$ 和 $q$ 递归地继续分解下去。

不妨构造伪随机数列 $a_{i} = f_{a_{i - 1}} \ mod\ N$ , 其中 $f(x) = x ^ {2} + c$ ($c$ 为一常数)。 而另一个数列 $\{a_{n} mod\ p\}$ 客观存在 ，由生日悖论我们可知 $\{a_{n}\}$ 的的循环节是 $O(\sqrt{N})$ 级别的 , 而 $\{a_{n} mod\ p\}$ 的循环节长度是 $O(\sqrt{p})$ 级别的。

假设存在两个位置 $i,j$ 使得 $a_{i} mod \ p = a_{j} mod \ p$ 且 $a_{i} \neq a_{j}$ , 取 $gcd(a_{i} - a_{j} , N)$ ， 就得到 $N$ 的一个非平凡因子。

因此我们要做的其实是找出 $\{a_{n} mod \ p\}$ 的循环节 ， 不妨使用弗洛伊德判环法 ，计算 $gcd(x_i-x_{2i},N)$。

若 $gcd(x_i-x_{2i},N) = 1$ , 那么将 $i$ 加一
若 $gcd(x_i-x_{2i},N) = N$ , 说明 $i$ 和 $2i$ 同时在两个数列的循环节上。 需要调整随机函数 $f$。
否则直接返回 $gcd(x_i-x_{2i},N)$。

因此我们期望用 $O(\sqrt{p})$ 个 $i$ 分解出 $N$ 的一个非平凡因子。 Pollard's Rho Algorithm 算法分解一个因子的复杂度是 $O(N^{\frac{1}{4}}*\alpha(N))$ 的。

事实上 , 可以继续优化

我们拟定一个参数 $\beta$，计算每 $\beta$ 个 $x_i−x_{2i}$ 的乘积对 $N$ 取模的结果 $prod$。

若 $gcd(prod,N) = 1$ ，则说明这 $\beta$ 个 $x_{i}−x_{2i}$ 与 $N$ 的 gcd 均为 1 。
若 $gcd(prod,N) \neq 1$ ，那么我们就找到了 $N$ 的一个非平凡因子 $gcd(prod,N)$
否则，即 $gcd(prod,N) = N$ ，我们不知道此时我们是否需要重新进行算法，需要回到 $\beta$ 次操作之前。

故算法产生一次有效的分解的期望时间复杂度被优化至了 $O(N^{\frac{1}{4}}+\frac{N^{\frac{1}{4}}*\alpha(N)}{\beta}+\beta*\alpha(N))$ 。

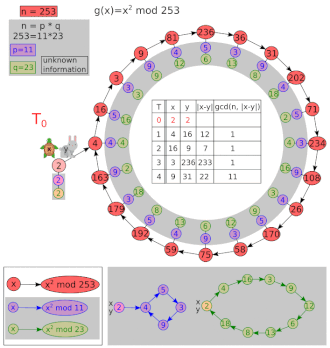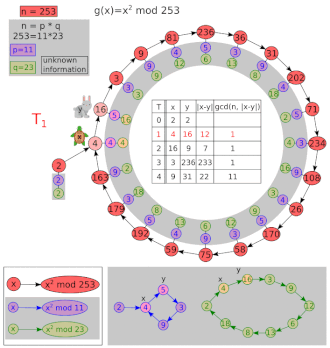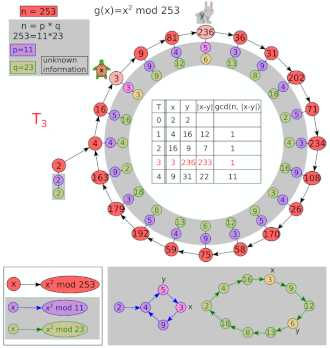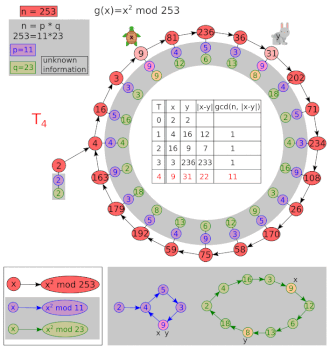
下面是 Pollard's Rho Algorithm 的一个演示图 ， 相信会有助于您更好地理解。 来源为 Wikipedia