Codeforces Round 633 题解
[题目链接]
http://codeforces.com/contest/1338
[题解]
\(A\)
不妨令 \(b_{i}\) 表示第 \(i\) 个数被加上了多少.
显然有 \(a_{i} + b_{i} \geq a_{i - 1} + b_{i - 1}\)
令 \(b_{1} = 0\) , 可以得到最优的 \(b\).
时间复杂度 \(O(N)\)
\(B\)
首先考虑最小值.
若叶子间两两距离为偶数 , 那么显然只要用一种权值.
否则 , 注意到 \(1 \oplus 2 \oplus 3 = 0\) , 将深度奇数的叶子权值赋 \(1\) , 偶数赋 \(2\) , 其余赋 \(3\) , 就构造出了一组解. 不难发现没有比这更优的方案.

然后考虑最大值.
显然对于有相同父亲的叶子节点 , 权值必然相同.
否则 , 由于值域无限大 , 必然可以找到一种方案使得其余点权两两不同.
树形 \(DP\) 即可.
时间复杂度 \(O(N)\)
\(C\)
打表 , 发现三元组 \((a , b , c)\) 分别是 :
1 2 3
4 8 12
5 10 15
6 11 13
7 9 14
16 32 48
17 34 51
18 35 49
19 33 50
20 40 60
21 42 63
22 43 61
23 41 62
24 44 52
25 46 55
26 47 53
27 45 54
28 36 56
29 38 59
30 39 57
31 37 58
64 128 192
....
我们将每三个数称作一组, 依照换行的位置分成数块. 三个数分别称作 \(a , b , c\) 那么首先可以发现
每一块内第一组中的 \(a\) 是 \(2\) 的偶数次幂, \(b\) 是 \(c\) 的两倍.
每一块中元素个数是 \(2\) 的偶数次幂…
每一块内, 除去第一组以外, \(a\) 的值较上一组增加 \(1\).
此时可以快速确定 \(a\) 的值 , 只需判定 \(N\) 在哪一块内, 然后计算即可.
考虑到 \(a \oplus b = c\) , 只需得到 \(b\) 的值即可计算 \(c\).
因此现在的问题在于计算 \(b\) 的值. 将 \(b\) 的值单独以二进制的形式列出 ,
发现从低位到高位, 每两位进行考虑. 对于小数据, 后两位形同并以此循环. 观察更高位, 也是依照这样的顺序, 只是重复的次数增加, 且重复的次数也是 \(2\) 的幂.
于是可以从低位到高位计算 \(b\).
时间复杂度 \(O(logN)\)
\(D\)
首先贡献必然是这样的形式 :
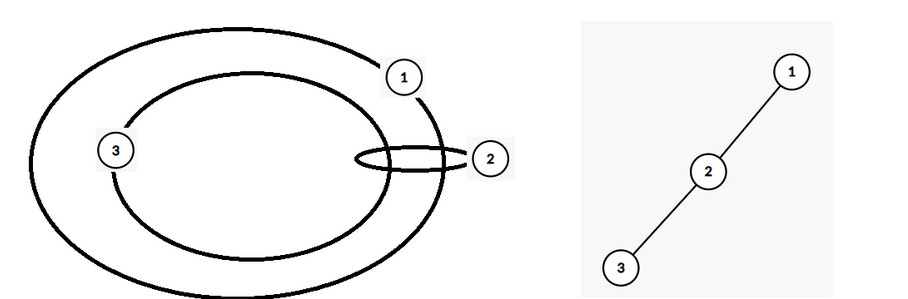
考虑题目中有哪些限制?
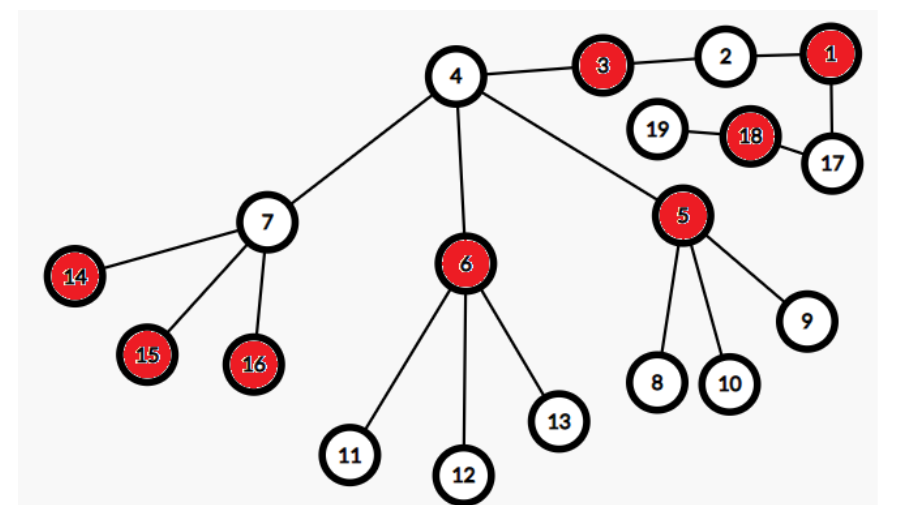
三个三叉子树 , 显然只有一棵可以被完全选入.
不难发现答案必然是某条路径和与这条路径距离为一的点构成联通块的最大独立集大小.
记 \(dp_{u , 0 / 1}\) 表示以 \(u\) 为根的子树 , \(u\) 是否在独立集中 , 最大能选多少点.
时间复杂度 \(O(N)\)
\(E\)
首先 , 竞赛图缩点后会形成一个链状 \(DAG\).
同时 , 若干个点的导出子图中有环 , 其中也必然存在三元环.
记 \(\mathrm{in}(x) = \{ u \mid u \to x \} , \deg(x) = |\mathrm{in}(x)|\)
引理 \(1\) : \(in(x)\) 无环
证明 \(1\) : 若有环 , 必然存在一个三元环向 \(x\) 连边.
将链状 \(DAG\) 依次编号为 \(S_1, S_2, \ldots , S_k\)
显然 , 除了 \(S_{1}\) , 其他联通分量只包含 \(1\) 个点.
这样 , 可以很方便地计算 \(S_2\) 至 \(S_k\) 中的点对答案的贡献.
现在只需考虑 \(S_{1}\) 了 , 也就是说原图是一张强连通图.
令 \(x\) 为 \(deg\) 最大的点 , 若有多个 , 任选一个.
令 \(P = \{x\} \cup \mathrm{in}(x)\) , 以及 \(Q = V \setminus P\)
显然 \(\deg(x) = |P| - 1\) , \(P , Q\) 非空.
引理 \(2\) : 存在 \(u , v\) , 其中 \(v \in P, u \in Q\) , 满足 \(v \leftarrow u\)
证明 \(2\) : 反证法,假设不存在这样的边,也就是说 \(P\) 中所有点均向 \(Q\) 中所有点连边 , 与 \(\deg(x) = |P| - 1\) 矛盾。
不妨选择满足引理 \(2\) 的一点 \(v\) , \(R = [\mathrm{in}(v) \cap Q] , Q = S = Q \setminus R\)
可以画出图形 :
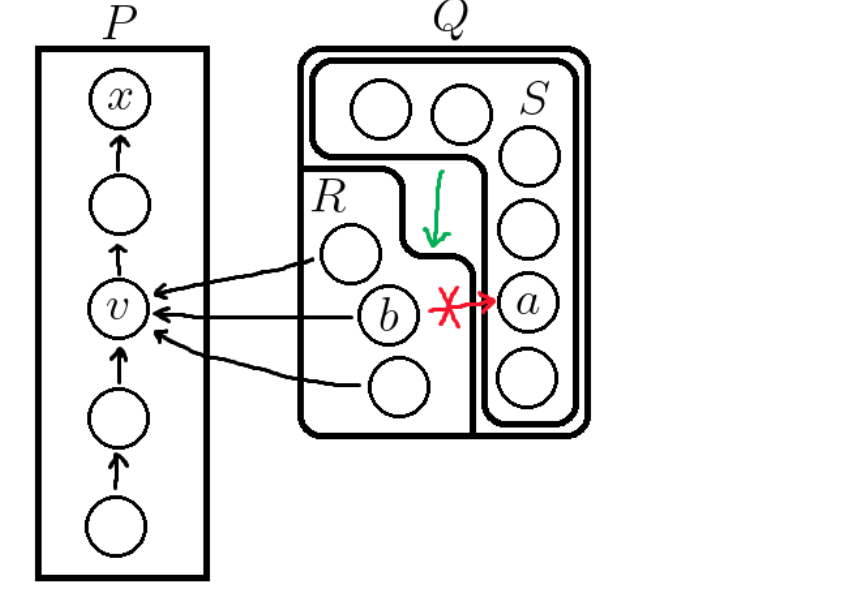
引理 \(3\) : \(S\) 中所有点向 \(R\) 中所有点连边.
证明 \(3\) : 假设一对 \(b , a\) 不满足 , 则 \((x , v , b , a)\) 不满足.
引理 \(4\) : \(R\) 无环, \(S\) 无环
证明 \(4\) : 由于 \(R \subseteq \mathrm{in}(v)\) , 所以无环 , 由于 \(S \subseteq \mathrm{in}(b)\) , 所以无环.
引理 \(5\) : \(P , Q\) 无环.
证明 \(5\) : 因为 \(P = \{x\} \cup \mathrm{in}(x)\) 所以无环 , \(R , S\) 之间无环且两部分无环 , 所以 \(Q\) 无环.
那么将 \(P , Q\) 重新编号 , 两边都是一条满的链.
令 \(inP(u)=in(u)\cap P,inQ(u)=in(u)\cap Q\)
引理 \(6\) : \(inQ(P_i)\) 为 \(Q\) 的一段后缀 , \(inP(Q_i)\) 为 \(P\) 一段后缀
可以总结出如下结论 :
\(dis(P_i,P_j)=1\Leftrightarrow i\lt j\)
\(dis(P_i,P_j)=2\Leftrightarrow j\lt i\land |inQ(P_i)|\ne |inQ(P_j)|\)
\(dis(P_i,P_j)=3\Leftrightarrow j\lt i\land |inQ(P_i)|=|inQ(P_j)|\)
\(dis(Q_i,Q_j)=1\Leftrightarrow i\lt j\)
\(dis(Q_i,Q_j)=2\Leftrightarrow j\lt i\land |inP(Q_i)|\ne |inP(Q_j)|\)
\(dis(Q_i,Q_j)=3\Leftrightarrow j\lt i\land |inP(Q_i)|=|inP(Q_j)|\)
\(dis(P_i,Q_j)+dis(Q_j,P_i)=3\)
时间复杂度 \(O(N ^ 2)\)
[代码]
\(A\)
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int MN = 2e5 + 5;
int N;
LL A[MN] , B[MN];
inline int qry(LL x) {
int ret = 0;
while ((1LL << ret) <= x) ++ret;
return ret;
}
int main() {
int T; scanf("%d" , &T);
while (T--) {
scanf("%d" , &N);
for (int i = 1; i <= N; ++i) scanf("%lld" , &A[i]);
int ans = 0;
B[1] = 0;
for (int i = 2; i <= N; ++i) {
B[i] = max(0LL , B[i - 1] + A[i - 1] - A[i]);
ans = max(ans , qry(B[i]));
}
printf("%d\n" , ans);
}
return 0;
}
\(B\)
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int MN = 2e5 + 5;
struct Edge {
int to , nxt;
} E[MN << 1];
int N , tot , head[MN] , f[MN][2] , ans = 1 , deg[MN];
inline void AddEdge(int u , int v) {
E[++tot] = (Edge) {v , head[u]};
head[u] = tot;
}
inline void DFS1(int u , int fa) {
if (!E[head[u]].nxt) f[u][0] = true;
for (int i = head[u]; i; i = E[i].nxt) {
int v = E[i].to; if (v == fa) continue; DFS1(v , u);
if (f[v][0] && f[u][0]) ans = 3;
if (f[v][1] && f[u][1]) ans = 3;
f[u][0] |= f[v][1]; f[u][1] |= f[v][0];
}
}
inline void DFS2(int u , int fa) {
if (!E[head[u]].nxt) {
if (u == 1) ++deg[E[head[u]].to];
else ++deg[fa];
}
for (int i = head[u]; i; i = E[i].nxt) {
int v = E[i].to; if (v == fa) continue;
DFS2(v , u);
}
}
int main() {
scanf("%d" , &N);
for (int i = 1 , u , v; i < N; ++i) {
scanf("%d%d" , &u , &v);
AddEdge(u , v) , AddEdge(v , u);
}
DFS1(1 , 0);
printf("%d " , ans);
ans = N - 1; DFS2(1 , 0);
for (int i = 1; i <= N; ++i)
if (deg[i]) ans -= deg[i] - 1;
printf("%d\n" , ans);
return 0;
}
\(C\)
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
LL N , f[] = {0 , 1 , 2 , 3 , 4 , 8 , 12 , 5 , 10 , 15 , 6 , 11 , 13 , 7 , 9 , 14} ,
foo[] ={0 , 2 , 3 , 1};
int main() {
int T; scanf("%d" , &T);
while (T--) {
scanf("%lld" , &N);
LL val = N;
if (N <= 15) {
printf("%lld\n" , f[N]);
continue;
}
LL now = 0;
while (val) val /= 4LL , ++now;
LL tmp = (N + 2) / 3;
LL frm = (1LL << (2 * (now - 1))) + (N - (1LL << (2 * (now - 1)))) / 3;
if (N % 3 == 1) printf("%lld\n" , frm);
else {
LL sx = (N - (1LL << (2 * (now - 1)))) / 3;
LL tmp = (1LL << (2 * now - 1));
LL cur = 1;
while (sx) tmp += cur * foo[sx % 4] , sx /= 4 , cur *= 4LL;
if (N % 3 == 2LL) printf("%lld\n" , tmp);
else printf("%lld\n" , frm ^ tmp);
}
}
return 0;
}
\(D\)
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int MN = 1e6 + 5;
int N , f[MN][2] , ans;
vector < int > g[MN];
inline void solve(int u , int fa) {
int ch = (int) g[u].size() - (fa != 0);
f[u][1] = 1; f[u][0] = ch;
for (int v : g[u]) {
if (v == fa) continue; solve(v , u);
ans = max(ans , f[u][0] - 1 + (fa != 0) + max(f[v][0] , f[v][1]));
ans = max(ans , f[u][1] + f[v][0]);
f[u][0] = max(f[u][0] , max(f[v][0] , f[v][1]) + ch - 1);
f[u][1] = max(f[u][1] , f[v][0] + 1);
}
ans = max(ans , max(f[u][0] , f[u][1]));
}
int main() {
scanf("%d" , &N);
for (int i = 1; i < N; ++i) {
int u , v;
scanf("%d%d" , &u , &v);
g[u].emplace_back(v) , g[v].emplace_back(u);
}
solve(1 , 0);
printf("%d\n" , ans);
return 0;
}
\(E\)
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
#define rep(i , l , r) for (int i = (l); i < (r); ++i)
const int MN = 8005;
char s[MN];
int N , deg[MN] , bel[MN] , num[MN];
vector < bool > A[MN];
int que[MN] , lb , rb;
LL ans;
int main() {
scanf("%d" , &N);
for (int i = 1; i <= N; ++i) {
scanf("%s" , s + 1);
A[i].resize(N + 1);
for (int j = 1; j <= N / 4; ++j) {
int x = isdigit(s[j]) ? s[j] - '0' : s[j] - 'A' + 10;
for (int k = 3; k >= 0; --k)
A[i][4 * j - k] = x >> k & 1;
}
}
for (int i = 1; i <= N; ++i)
for (int j = 1; j <= N; ++j)
if (A[i][j]) ++deg[j];
int C = N;
lb = 1 , rb = 0;
for (int i = 1; i <= N; ++i) if (!deg[i]) que[++rb] = i;
while (lb <= rb) {
int u = que[lb++];
bel[u] = 3;
ans += (614LL * N + 1) * --C;
for (int i = 1; i <= N; ++i) if (A[u][i])
if (!--deg[i]) que[++rb] = i;
}
if (!C) {
printf("%lld\n" , ans);
return 0;
}
int x = max_element(deg + 1 , deg + 1 + N) - deg;
for (int i = 1; i <= N; ++i) if (bel[i] != 3)
bel[i] = i == x || A[i][x] ? 1 : 2;
for (int i = 1; i <= N; ++i) if (bel[i] != 3)
for (int j = 1; j <= N; ++j) if (i != j && bel[j] != 3)
if (bel[i] != bel[j] && A[i][j]) ++num[j];
for (int i = 1; i < N; ++i) if (bel[i] != 3)
for (int j = i + 1; j <= N; ++j) if (bel[j] != 3)
ans += 3 + (bel[i] == bel[j] && num[i] == num[j]);
printf("%lld\n" , ans);
return 0;
}



