[WC2021] 括号路径

[题目链接]

https://loj.ac/p/3462

[题解]

首先有一个显然的观察 : 若 \((u , v)\) 合法 ， 那么 \((v , u)\) 同样合法。

考虑一种简单情况 :

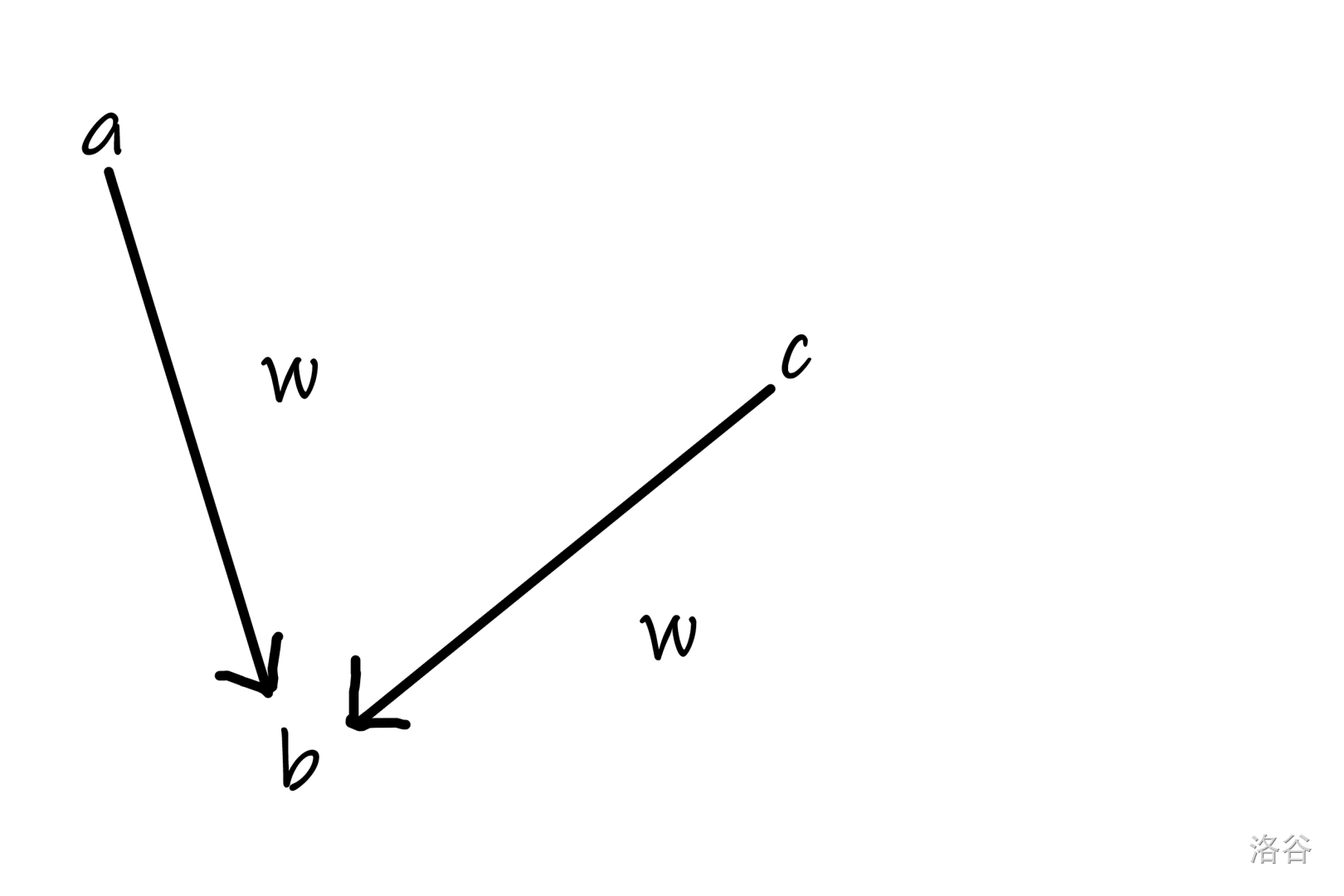
如图 ， \(a , c\) 是一条合法路径。 那么不妨将 \(a , c\) 合并 ， 用并查集维护 ， 再放入一个队列中与其它点合并即可。

时间复杂度 : \(O(NlogN)\)

[代码]

#include <bits/stdc++.h>

using namespace std;

typedef long long LL;

#define rep(i , l , r) for (int i = (l); i < (r); ++i)

const int MN = 3e5 + 5;

typedef pair < int, int > pii;
#define mp make_pair
#define F first
#define S second

int N, M, K, fa[MN], cnt[MN];
queue < pii > q;
unordered_map < int, int > e[MN];

inline int find(int x) {
    return fa[x] == x ? x : fa[x] = find(fa[x]);
}
inline void merge(int x, int y) {
    x = find(x), y = find(y);

    if (x == y)
        return;

    if (e[x].size() < e[y].size())
        swap(x, y);

    for (auto it : e[y])
        if (e[x].count(it.F))
            q.push(mp(e[x][it.F], it.S));
        else
            e[x][it.F] = it.S;

    fa[y] = x;
    e[y].clear();
}

int main() {

    scanf("%d%d%d", &N, &M, &K);

    for (int i = 1; i <= N; ++i)
        fa[i] = i;

    for (int i = 1, u, v, w; i <= M; ++i) {
        scanf("%d%d%d", &u, &v, &w);
        swap(u, v);

        if (e[u].count(w))
            q.push(mp(e[u][w], v));
        else
            e[u][w] = v;
    }

    while (q.size()) {
        pii x = q.front();
        q.pop();
        merge(x.F, x.S);
    }

    for (int i = 1; i <= N; ++i)
        ++cnt[find(i)];

    LL ans = 0;

    for (int i = 1; i <= N; ++i)
        ans += 1ll * cnt[i] * (cnt[i] - 1) / 2;

    printf("%lld\n", ans);
    return 0;
}