[CF506E] Mr. Kitayuta's Gift
[题目链接]
https://codeforces.com/contest/506/problem/E
[题解]
首先假设 \(|s| + n\) 为偶数。
考虑朴素动态规划 ， 令 \(dp_{i , l , r}\) 表示用了 \(i\) 个字符 ， 字符串 \(S\) 还剩 \([l , r]\) 这段区间的方案数 ， \(g_{i}\) 表示用了 \(i\) 个字符匹配了 \(S\) 的方案数。 转移不赘述了。
用矩阵乘法优化 ， 可以得到一个 \(O(|S| ^ 6log|S|)\) 的做法。
注意到这个 \(DP\) 实质上实在一个有限状态自动机 (\(DFA\)) 上匹配的过程。 如图 ：
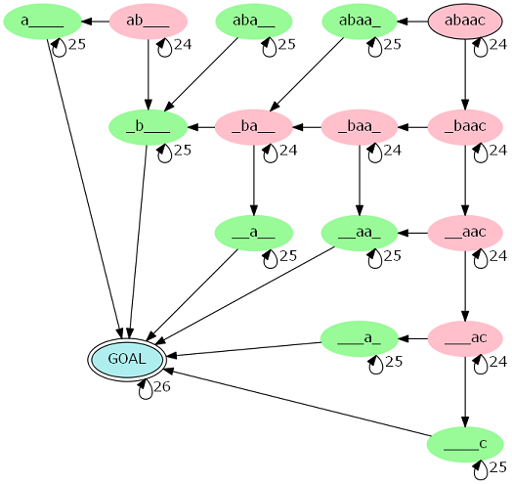
考虑压缩自动机 ， 注意到一条有 \(k\) 个红点的路径必然对应着 \(\rfloor \frac{|s| - k}{2} \rfloor\) 个绿点 ， 同时最终连接终点的点一定是绿点。
对于两条红点个数相同的链 ， 它们对答案的贡献与红点的具体位置无关 ， 因为其自环数及点数都相同。 因此只有 \(O(|S|)\) 条本质不同的链。
令 \(h_{i , l , r}\) 表示从起点走到 \((l , r)\) 对应的节点的路径中 ，有多少条经过了 \(i\) 个红点 ， 可以用记忆化搜索的方式求得 ， 时间复杂度 \(O(|S| ^ 3)\)。
现在我们只有了 \(O(|S|)\) 条本质不同的链 ， 同时知道了每种链的条数 ， 可以对每条链进行矩阵乘法 ， 时间复杂度降为 \(O(|S| ^ 4log|S|)\)。
但这样仍然是不行的 ， 考虑建出一个 \(O(|S|)\) 个节点的自动机 (如图) ：
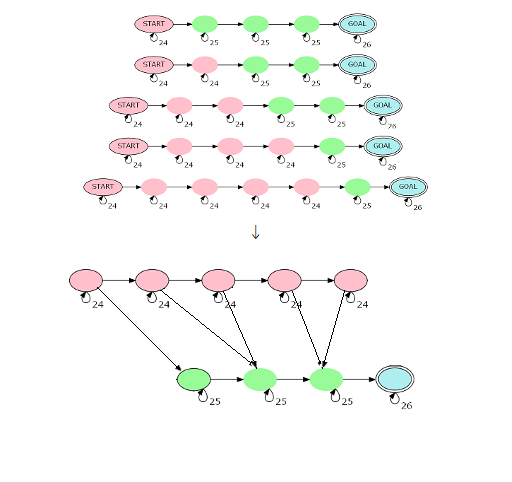
这样就可以做到 \(O(|S| ^ 3log|S|)\) 了！
最后考虑奇数的情况 ， 相比起偶数的情况 ， 奇数的情况相当于限制了最后一步不能从一个 \(2\) 个字符的绿色节点转移而来 ， 那么去除自动机终点的自环 ， 求出这样的方案数减去即可。
但我们仍然不能通过此题。 考虑将节点编号 ， 每条边都从编号小的节点连向编号大的。 那么这样转移矩阵就是一个上三角矩阵。 不用全部清零 ， 复杂度被乘了一个 \(\frac{1}{6}\) 的常数。
问题得到了完美的解决。
[代码]
#include<bits/stdc++.h>
using namespace std;
#define rep(i , l , r) for (int i = (l); i < (r); ++i)
typedef long long LL;
const int MN = 207 , MM = 307 , mod = 10007;
int n , m , k;
char s[MN];
bool vis[MN][MN][MN];
int h[MN][MN][MN] , f[MM] , g[MM][MM] , F[MM] , G[MM][MM];
inline void inc(int &x , int y) {
x = x + y < mod ? x + y : x + y - mod;
}
inline void dec(int &x , int y) {
x = x - y >= 0 ? x - y : x - y + mod;
}
inline int ceil(int n) {
return (n >> 1) + (n & 1);
}
inline int H(int i , int l , int r) {
if (i < 0) return 0;
if (vis[i][l][r]) return h[i][l][r];
vis[i][l][r] = 1;
if (l == 1 && r == m) return h[i][l][r] = !i;
if (l != 1 && s[l - 1] != s[r]) inc(h[i][l][r] , H(i - 1 , l - 1 , r));
if (r != m && s[l] != s[r + 1]) inc(h[i][l][r] , H(i - 1 , l , r + 1));
if (l != 1 && r != m && s[l - 1] == s[r + 1]) inc(h[i][l][r] , H(i , l - 1 , r + 1));
return h[i][l][r];
}
inline void mul(int f[MM] , int g[MM][MM]) {
int a[MM];
memset(a , 0 , sizeof(a));
for (int j = 1; j <= k; ++j)
for (int i = 1; i <= k; ++i)
inc(a[i] , 1ll * f[j] * g[j][i] % mod);
for (int i = 1; i <= k; ++i) f[i] = a[i];
}
inline void mul(int g[MM][MM]) {
int a[MM][MM];
memset(a , 0 , sizeof(a));
for (int i = 1; i <= k; ++i)
for (int o = i; o <= k; ++o)
for (int j = o; j <= k; ++j)
inc(a[i][j] , 1ll * g[i][o] * g[o][j] % mod);
for (int i = 1; i <= k; ++i)
for (int j = 1; j <= k; ++j)
g[i][j] = a[i][j];
}
inline void Exp(int o) {
while (o) {
if (o & 1) mul(f , g);
mul(g); o >>= 1;
}
}
int main() {
scanf("%s%d" , s + 1 , &n); m = strlen(s + 1); k = m + ceil(m);
for (int i = 0; i < m; ++i) {
int c = 0;
for (int j = 1; j <= m; ++j) {
inc(c , H(i , j , j));
if (j != m && s[j] == s[j + 1]) inc(c , H(i , j , j + 1));
}
if (i) {
g[i][k - ceil(m - i)] = c , g[i][i] = 24;
if (i != 1) g[i - 1][i] = 1;
else f[i] = 1;
} else {
f[m] = c , g[k][k] = 26;
for (int j = m; j < k; ++j) g[j][j + 1] = 1 , g[j][j] = 25;
}
}
if ((n + m) & 1) {
for (int i = 1; i <= k; ++i) F[i] = f[i];
for (int i = 1; i <= k; ++i)
for (int j = 1; j <= k; ++j)
G[i][j] = g[i][j];
}
Exp(ceil(n + m));
if (!((n + m) & 1)) { printf("%d\n" , f[k]); return 0; }
int ans = f[k];
for (int i = 1; i <= k; ++i) f[i] = F[i];
for (int i = 1; i <= k; ++i)
for (int j = 1; j <= k; ++j)
g[i][j] = G[i][j];
for (int i = 0; i < m; ++i) {
int c = 0;
for (int j = 1; j <= m; ++j)
if (j != m && s[j] == s[j + 1]) inc(c , H(i , j , j + 1));
if (i) g[i][k - ceil(m - i)] = c;
else f[m] = c , g[k][k] = 0;
}
Exp(ceil(n + m));
printf("%d\n" , (ans - f[k] + mod) % mod);
return 0;
}
