博弈论 学习笔记

基础概念

     \(P-Position\) : 必胜的位置

     \(N-Position\) : 必败的位置

性质 ： 对于一个 \(N-Position\) , 其转移边指向的都是 \(P-Position\) , 而对于一个 \(P-Position\) , 其转移边至少可以到达一个 \(N-Position\)。

模型 ：

巴什博弈

     有一堆石子 ，总个数是 \(N\)，两名玩家轮流在石子堆中拿石子，每次至少取 \(1\) 个，至多取 \(M\) 个。取走最后一个石子的玩家为胜者。判定先手和后手谁胜。

     结论 ： 若 \((M + 1) | N\) , 先手必败 ， 否则必胜

     简要证明 ： 若 \((M + 1) | N\) ， 无论先手拿了多少个 （假设为 \(X\)) , 后手必然可以拿 (\(M + 1 - X\)) 个。 这样就能把空决策集合留给先手。 否则 ， 先拿走余数个即可。

威佐夫博弈

     结论 ： 先手必败的状态一定形如 \(([i * \phi] , [i * ϕ ^ 2])\)。其中 \(\phi = \frac{ \sqrt{5} + 1}{2}\)。

     证明略。

尼姆博弈

     有 \(N\) 堆石子 \(x_{1} , x_{2} , x_{3} , ... , x_{n}\)，两人轮流取 ，每次可以从任意一堆石子中取走至少一个石子 ，问先后手谁胜。

     结论 ： 若 \(x_{1} \oplus x_{2} \oplus x_{3} ..... \oplus x_{n} = 0\) , 先手必败 ， 否则必胜。

     证明 ： 首先当没有石子的时候，先手必败，此时所有石子的异或和为 \(0\) ，这个是P状态。接下来证明任意一个 \(N\) 状态至少能够达到一个 \(P\) 状态。

     假设当前所有石子个数的异或和为 \(K\) ，那么 ，必定存在一个 \(x_{i}\) 满足 \(x_{i}\) 二进制位上存在k的最高位，并且不难证明 \(x_{i} \oplus K < x_{i}\) ，那么，将 \(x_{i}\) 异或上 \(K\) 之后，剩下所有的数的异;

     或和恰好为 \(0\) ，又回到了一个 \(P\)状态。 而一个 \(P\) 状态的异或和为 \(0\)，任何一个数减小之后异或和一定不为 \(0\)，所以可以证明任何一个 \(P\) 状态的后继状态都是 \(N\) 状态。

     综上 ，异或和为 \(0\) 的状态先手必败，其他情况先手必胜。

     变形 ：

     石子上限为 \(M\)。

     解法 ： 这个问题相当于 \(Bash\) 博弈和 \(Nim\) 博弈的综合。 直接对每堆石子取模按照 \(Nim\) 做就可以解决了。

阶梯博弈 ：

     博弈在阶梯上进行 ，每次可以将一堆的若干石子移动到上一阶去 ，决策集合为空者输。

     结论 ： 忽略偶数编号的阶梯 ， 对奇数编号阶梯做 \(Nim\) 博弈即可。

     证明 ： 首先终止态是 \(0\) 号阶梯 ， 是一个偶数阶梯 ， 因此若对方移动了偶数阶梯的石子 ， 那么直接移动等量的到上一层去 ， 并不会造成影响。 如果移动了奇数级阶梯 ， 那么相当于普通尼姆博弈。

树的删边游戏 ：

     给定一个 \(N\) 个节点的有根树，两人轮流删边，删去边之后，不和根节点联通的部分都会被移除。不能操作者输，判断胜负。

     结论 ： 定义叶子节点的 \(SG\) 值为 \(0\) ，其他所有节点的 \(SG\) 值为它所有儿子的 \(SG\) 值加 \(1\) 后的异或和。

     证明 ： https://wenku.baidu.com/view/379e8baaa58da0116d174924.html

\(SG\) 函数 ：

     \(SG\) 定理 ： 对于当前游戏 \(X\) ，它可以拆分成若干个子游戏 \(x_{1} , x_{2} , x_{3} , ... , x_{n}\) 。那么 \(SG(X) = SG(x_{1}) \oplus SG(x_{2}) .... \oplus \ SG(x_{n})\)。

     对于一个子游戏的某个状态而言 ， 若其无转移边 ， 其 \(SG\) 值为 \(0\) , 否则为 \(mex \{SG(y) | (x , y) \in E\}\)。 \(mex\) 运算表示一个集合最小未出现的整数。

     \(SG\) 函数非 \(0\) 的位置为必胜点。

例题 ：

\(P3185\)

     来自湖南 \(2007\) 省选。

     题解 ：

     不难发现每件物品其实是独立的 ， 因此暴力求解每颗石子的 \(SG\) 值 ， 异或起来即可。

     时间复杂度 : \(O(N ^ 3)\)。

\(CF1149E\)

题解 ：

     注意到原图是一张 \(DAG\) , 那么不妨直接将没有出度的点的 \(SG\) 值设为 \(0\) , 求解每个节点的 \(SG\) 函数值。

     定义数组 \(s\) , 其中 \(s_{i}\) 表示 \(SG\) 值为 \(i\) 的点的权值异或和。

     结论 ： 当 \(s_{1} \oplus s_{2} \oplus s_{3} .... \oplus s_{m} = 0\) 时必败 ， 否则必胜。

     证明 ：

     首先最后的 \(N - Position\) 满足该条件。

     不妨按照定义证明 ： 对于一个 \(N - Position\) , 其必然会走到一个 \(P - Position\) ， 或者直接宣告失败。 而对于一个 \(P - Position\) , 必然满足一个 \(s_{i}\) 使得 \(s_{i} \neq 0\) , 找到满足该条件最大的 \(i\) ， 在该点对应的集合中必然能找

     到一个 \(a_{j} \oplus s_{i} < a_{j}\)。 将其修改 ， 接着枚举其转移边 （因为是最大的 ， 所以每种权值都能被枚举到） ， 修改每个转移边的 \(a\) 值 ， 这样就到达了一个 \(N - Position\) 。

     时间复杂度 : \(O(N + M)\)

\(CF1037G\)

题解 :

     预处理每个后缀 ， 前缀 ， 每种字母相邻间隔的 \(SG\) 值。

     这样就可以方便地算出任意一段区间的 \(SG\) 函数值。

     附一段代码 ：

     时间复杂度 : \(O(N * ALPHA)\)

\(CF1091H\)

题解 ：

     首先这不是 \(ICG\)。因为双方的决策不一样 ， 因此无法直接用 \(SG\) 函数做。

     不妨考虑转化 ， 由于关心的仅仅是相邻两数之差 ， 因此可以用二元组 \((a , b)\) 表示状态。

     这样对于一个 \((a , b)\) , 只会转移到 \((a - k , b)\) 或 \((a , b - k)\)。

     那么这就是一个近似于 \(Nim\) 的游戏了。 只是取的数有限制而已。

     用筛法预处理所有的 "好" 数。 这会花费 \(O(N)\) 的时间。

     观察到 \(2 * 10 ^ 5\) 以内的 \(SG\) 值不超过 \(100\) , 因此不妨对于每种 \(SG\) 值维护一个 \(bitset\) , 表示能否转移到某个位置。

     这样做的时间复杂度是 \(O(\frac{N ^ 2}{w})\) 的。

\(LOJ3114\)

题解 ：

     来自山东 \(2019\) 省选。

     不妨将空位看成石子 ， 将 “金币” 看成隔板 ， 那么移动一件物品相当于将移动了某堆中的若干石子到前面一堆石子中。

     不难发现这实质上是一个阶梯博弈问题。 阶梯博弈的一般解法是忽略偶数堆的石子 ，计算奇数堆石子的 \(Nim\) 和。

     对于这题而言 ，我们并不关心 “隔板” 的具体位置。只关心每堆石子的数量。

     所以要求的就是一个形如 \(N\) 枚石子分为 \(M\) 堆 ， 且奇数堆异或起来是 \(0\) 的方案数的问题。

     不妨按位枚举 ， 并记 \(dp_{i , j}\) 表示前 \(i\) 为 ， 用了 \(j\) 枚石子 ，异或起来是 \(0\) 的方案数。 这样直接转移即可。

     具体实现时需要用到一些组合数学的知识 ， 不赘述了。

     时间复杂度 : \(O(NMlogN)\)

\(AGC016F\)

题解 ：

     首先补集转化 ， 计算两个点的 \(SG\) 值不同的方案数。

     枚举边集不太可做 ， 考虑枚举点集。

     记 \(f_{S}\) 表示只考虑集合 \(S\) 内的点 ， \(1\) 和 \(2\) 号点的 \(SG\) 值相同的方案数。

     考虑枚举子集 \(T\) , 使得 \(T\) 集合中的 \(SG\) 值都不为 \(0\) ， 并令 \(U\) 为 \(T\) 补集。

     转移可以分 \(4\) 类讨论。不赘述了。

     时间复杂度 : \(O(3 ^ N * N ^ 2)\)

\(AGC043C\)

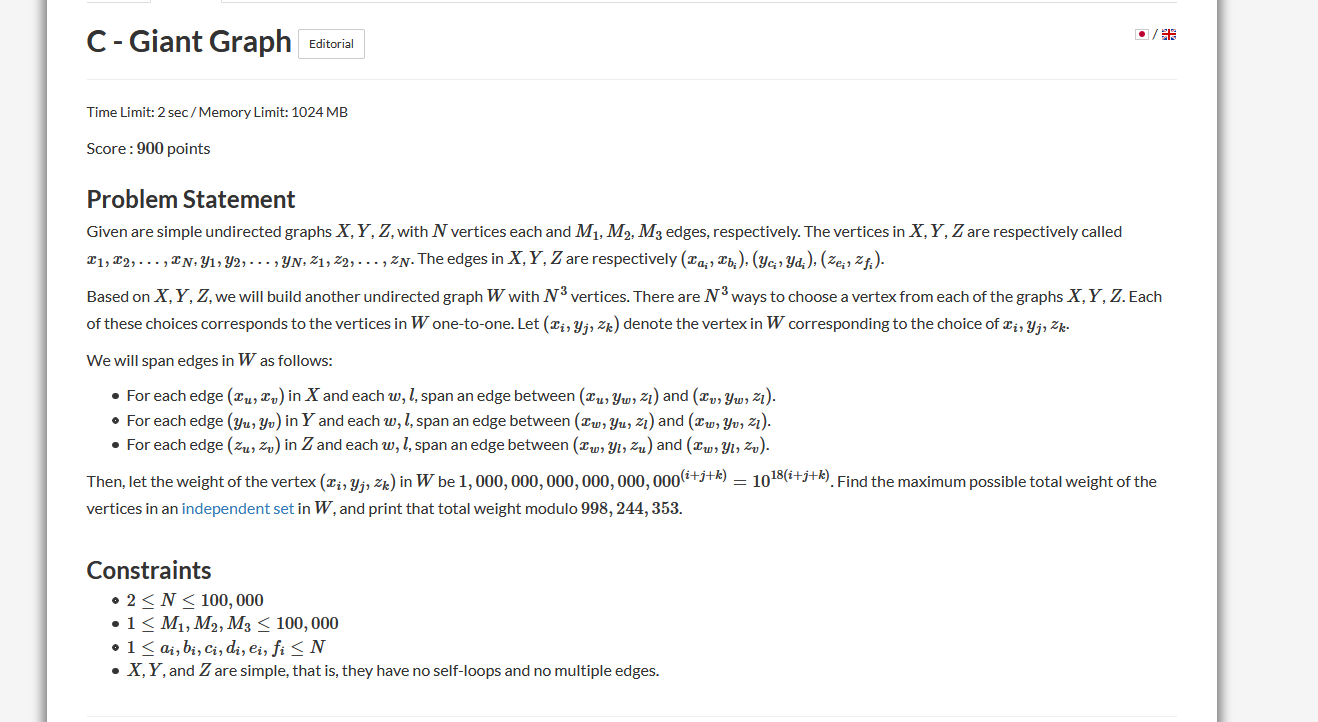
题解 ：

     一个节点的价值的底数 \(10 ^ {18}\) 可以看做 \(+\infty\)。 也就是说 ， 贪心策略就是优先选取权值较大的点。

     那么就有一个 \(O(N ^ 3)\) 的做法了 ， 从大到小枚举 \(S\) , 依次选点。

     调整边的顺序 ， 将权值小的点连向大的 ， 这样就构成了一张有向无环图 (\(DAG\))。

     我们重新梳理算法流程 ：

     按权值倒着选点 ， 如果这个点的所有出边都未选 ， 将这个点标记为已选 ， 否则将这个点标记为 "不可选中"。

     不难发现这个过程就是博弈的过程 ， 前者代表着 \(N-Position\) , 而后者代表着 \(P-Position\)。

     进一步地 ， 发现每个点的坐标每次只有一维会变动 ， 因此这是一个 \(ICG\) , 可以拆分为三个游戏的游戏和。

     因此要求的就是 \(\sum_{i}\sum_{j}\sum_{k}{[i \oplus j \oplus k = 0]10 ^ {18(i + j + k)}}\)。

     可以用 \(FWT\) 进行异或卷积 ， 也可以通过观察得到 \(SG\) 函数值不超过 \(500\) , 暴力枚举计算答案。

     时间复杂度 : \(O(N + M)\)

题解 ：

     首先不妨将棋盘黑白染色。

     一个结论是 : 后手必胜当且仅当存在最大匹配不包括当前节点。

     为什么是这样呢？ 当存在一组最大匹配不包含起点 \(u\) 时 ，先手从 \(u\) 出发 ，先随便走一条非匹配边 ，此时后手一定往下走一条匹配边 ，先手再走一条非匹配边 ，如此往复直到最后先手无边可走 。此时后手必胜 。为什

么后手总能找到下一条匹配边 ？因为否则它们走出的路径就由非匹配边开头 ，非匹配边结束——这是一条增广路！显然不符合 "最大匹配" 这一条件。

     把 \(u\) 去掉 ， 看原图是否能增广 ， 若能 ， 说明找到了新的最大匹配。 否则不能。

     时间复杂度 ： \(O(N ^ 4)\)

\(CF1451F\)

题解 ：

     如图 ，

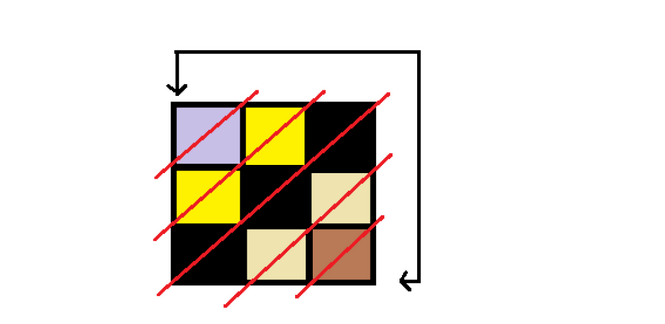
     若干条对角线将棋盘分割为若干个类似于 \(Nim\) 的游戏和。 具体做法类似于 \(CF1149E\)。 时间复杂度 : \(O(NM)\)