同调代数笔记1
范畴论,尤其是阿贝尔范畴,是同调代数的基石。基础的范畴论包含了以下概念:
范畴
一个范畴\(\mathcal{C}\)包含对象\(\text{obj}(\mathcal{C})\),和态射\(\text{Hom}(A, B)\),其中\(A,B\in \text{obj}(\mathcal{C})\),态射必须满足
- 每个对象\(A\in\text{obj}(\mathcal{C})\)存在\(1_A \in \text{Hom}(A, A)\),使得\(f1_A = f\)且 \(1_Af = f\)
- 复合运算是结合的,即\(f\in\text{Hom}(A, B), g\in\text{Hom}(B, C), h\in\text{Hom}(C, D)\),则
我们发现,态射的概念和幺半群十分相似,但幺半群中每个元素皆可相乘,而态射的复合必须匹配定义域和值域。有了态射之后,我们还可以定义一些特殊的态射。注意这些概念并不考虑对象中的元素,而是通过态射的交换性构造:
- 如果态射\(f\in\text{Hom}(A, B)\)满足对任意\(g_1, g_2\in \text{Hom}(B, C)\)都有\(g_1 \circ f = g_2 \circ f\),以及对任意\(h_1, h_2\in \text{Hom}(D, A)\)都有\(f\circ h_1 = f\circ h_2\),就称\(f\)为零态射。
- 对于\(f\in\text{Hom}(A, B)\),如果任意\(g_1, g_2\in\text{Hom}(C, A)\)都满足\(f\circ g_1 = f\circ g_1 \Rightarrow g_1 = g_2\),则称\(f\)是单态射,记为\(↪\),其概念和单射类似。
- 对于\(f\in\text{Hom}(A, B)\),如果任意\(g_1, g_2\in\text{Hom}(B, C)\)都满足\(g_1 \circ f = g_2 \circ f \Rightarrow g_1 = g_2\),则称\(f\)是满态射,记为\(↠\),注意满态射不一定是满射,例如嵌入映射。
- 如果\(f\in\text{Hom}(A, B)\)既是单态射又是满态射,那么就称其为双态射。
- 如果\(f\in\text{Hom}(A, B), g\in\text{Hom}(B, A)\),并且\(gf = 1_A, fg = 1_B\),则称\(f, g\)是同构,记为\(\xrightarrow{\sim}\),并且\(g\)称为\(f\)的逆态射。
注意同构是双态射,但双态射不一定是同构,例如环范畴中\(\mathbb{Z}↪\mathbb{Q}\)是双态射但不是同构。如果一个范畴中的双态射都是同构,那么就称其为平衡范畴。
除此之外,我们还可以定义一些特殊的对象:对于\(A\in \text{obj}(\mathcal{C})\)
- 如果对任意\(B\in \text{obj}(\mathcal{C})\),在\(\text{Hom}(A, B)\)中有且仅有一个元素,那么就称\(A\)为起始对象。
- 如果对任意\(B\in \text{obj}(\mathcal{C})\),在\(\text{Hom}(B, A)\)中有且仅有一个元素,那么就称\(A\)为终止对象。
- 如果\(A\)既是起始对象又是终止对象,那么就称其为零对象。
- 如果对任意满态射\(X ↠ Y\)和态射\(P \to Y\),如果有唯一的态射\(P \to X\),就称\(P\)为投射对象。
![image]()
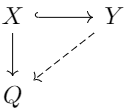
- 如果对任意单态射\(X ↪ Y\)和态射\(X \to Q\),如果有唯一的态射\(Y \to Q\),就称\(P\)为内射对象。
![image]()
投射对象和内射对象在同调代数中有重要用途。
注记:
- 范畴中对象的全体不一定是ZFC集合,也可能是真类,如果是前者我们称为小范畴,如果是后者则称为大范畴。
- 一个范畴\(\mathcal{C}\)中的部分对象和部分态射如果满足范畴的条件,可以称为\(\mathcal{C}\)的子范畴;如果子范畴\(\mathcal{S}\)的任意对象\(A, B\in \text{obj}(\mathcal{S})\)都满足\(\text{Hom}_\mathcal{S}(A, B) \cong \text{Hom}_\mathcal{C}(A, B)\),那么就称\(\mathcal{S}\)为满子范畴。
- 一个范畴\(\mathcal{C}\)的反范畴\(\mathcal{C}^{op}\),满足:
- 对于拓扑空间\(X\),开集范畴\(\text{Op}(X)\)的对象为\(X\)中的开集,态射为包含映射。
函子
函子是范畴之间的映射,分为共变函子和反变函子。共变函子\(T: \mathcal{C}\to \mathcal{D}\)的构造如下:对任意\(A \in \mathcal{C}\)都有\(T(A) \in \mathcal{D}\);对任意\(f \in \text{Hom}_\mathcal{C}(A, B)\)都有\(T(f) \in \text{Hom}_\mathcal{D}(T(A), T(B))\),并且满足
而反变函子\(T: \mathcal{C}\to \mathcal{D}\)则是:对任意\(A \in \mathcal{C}\)都有\(T(A) \in \mathcal{D}\);对任意\(f \in \text{Hom}_\mathcal{C}(A, B)\)都有\(T(f) \in \text{Hom}_\mathcal{D}(T(B), T(A))\),并且满足
我们有以下例子:
- 如果\(f\to T(f)\)是单态射,那么就称\(T\)是一个忠实函子,如果是满态射,就称\(T\)是一个满函子。如果存在忠实函子\(F: \mathcal{C}\to \mathbf{Set}\),那么就称\(\mathcal{C}\)为具体范畴。当我们用交换图证明时,我们其实是把范畴看作具体范畴。
- 令\(X \in \text{obj}(\mathcal{C})\),\(\text{Hom}(A, -)\)将对象\(X\)映射成\(\text{Hom}(A, X)\),将态射\(f\in \text{Hom}(X, Y)\)映射成态射的函数\(g \to g \circ f\),其中\(g\in \text{Hom}(A, X)\),这个取值为\(\mathbf{Set}\)的函子称为Hom函子。\(\text{Hom}(A, -)\)是一个共变函子,也可以定义反变函子\(\text{Hom}(-, B)\)。
- 如果一个共变函子\(F: \mathcal{C}\to \mathbf{Set}\)满足存在\(A\in \text{obj}(\mathcal{C})\)使得\(F\cong \text{Hom}(A, -)\),那么称\(F\)是可表函子,写成\(h_A\)。我们也可以对反变函子定义可表函子。
- 反变函子\(G: \text{Op}(X) \to \mathbf{Set}\)称为拓扑空间\(X\)上的预层。
- 设\(F: \mathcal{C} \to \mathcal{D}, G: \mathcal{D} \to \mathcal{C}\)是两个函子,如果对任意对象\(X\in \mathcal{C}, Y\in \mathcal{D}\)有\(\text{Hom}(FX, Y)\cong \text{Hom}(X, GY)\),那么称\(F, G\)是一对伴随函子,\(F\)称为\(G\)的左伴随,\(G\)称为\(F\)的右伴随。
自然变换
自然变换是函子之间的映射。假如\(S, T: \mathcal{C} \to \mathcal{D}\)是两个共变函子,那么自然变换\(\tau\)定义为:对任意\(A\in \text{obj}(\mathcal{C})\),\(\tau_A: S(A) \to T(A)\);对任意\(f\in\text{Hom}(A, B)\),\(\tau_A \circ S(f) = T(f) \circ \tau_B\)。类似也可以定义反变函子的自然变换。如果每个\(\tau_A\)都是同构,则称\(\tau\)为自然同构。
注意:由于后一个条件的存在,自然变换不一定存在,也不一定唯一。例如:令\(\mathcal{I} = 0 \to 1\)是2个对象和1个态射构成的范畴,令\(S: \mathcal{I} \to \mathcal{I}\)把两个都映射到0,\(T: \mathcal{I} \to \mathcal{I}\)把两个都映射到1。我们发现\(S,T\)不存在自然变换。
对于自然变换,我们有以下著名的米田引理
设\(A\in \mathcal{C}\),\(h_A\)是范畴\(\mathcal{C}\)上的可表函子,\(G: \mathcal{C}\to \mathbf{Set}\)是\(\mathcal{C}\)上的另一个函子,则有
\[\text{Nat}(h_A, G) \cong G(A) \]

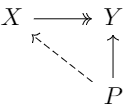

 浙公网安备 33010602011771号
浙公网安备 33010602011771号