深度学习中的常见激活函数

1 sigmoid

1.1 sigmoid函数的公式

\[f(x)= \frac{1}{1+e^{-x}} \]

1.2 sigmoid函数的导数公式

\[f'(x)= f(x)\cdot [1-f(x)] \]

1.3 sigmoid函数代码实现

class SigmoidActivator(object):
    
    def sigmoid(self,x):
        return 1.0/(1.0+np.exp(-x))

    def sigmoid_derivative(self,x):
        return self.sigmoid(x)*(1-self.sigmoid(x))

    def sigmoid_graph(self):
        x = np.arange(-8,8,1)
        y = self.sigmoid(x)
        y_derivative = self.sigmoid_derivative(x)
        plt.plot(x,y,'g:')
        plt.plot(x,y_derivative,'r-')
        plt.legend(['sigmoid', 'sigmoid_derivative'])
        plt.show()

效果图：

if __name__ == '__main__':
    x = 3
    
    # Sigmoid
    sig = SigmoidActivator()
    sig.sigmoid(x)
    sig.sigmoid_derivative(x)
    sig.sigmoid_graph()

2 tanh

2.1 tanh函数的公式

\[f(x)=\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}} \]

2.2 tanh函数的导数公式

\[f(x)=1-[f(x)]^{2} \]

2.3 tanh函数代码实现

class TanhActivator(object):

    def tanh(self,x):
        return 2.0/(1+np.exp(-2*x))-1.0

    def tanh_derivative(self,x):
        return 1-self.tanh(x)*self.tanh(x)

    def tanh_graph(self):
        x = np.arange(-8,8,1)
        y = self.tanh(x)
        y_derivative = self.tanh_derivative(x)
        plt.plot(x,y,'g:')
        plt.plot(x,y_derivative,'r-')
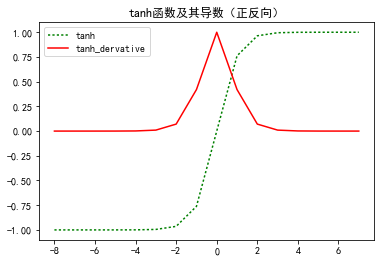
        plt.title("tanh函数及其导数（正反向）")
        plt.legend(['tanh','tanh_dervative'])
        plt.show()

效果图：

if __name__ == '__main__':
    x = 3
    
    #tanh
    tanh = TanhActivator()
    tanh.tanh(x)
    tanh.tanh_derivative(x)
    tanh.tanh_graph()

3 Relu

3.1 Relu函数的公式

\[f(x)=\left\{\begin{matrix} x, & x\geq 0\\ 0,& x< 0 \end{matrix}\right. \]

3.2 Relu函数的导数公式

\[f^{'}(x)=\left\{\begin{matrix} 1, & x\geq 0\\ 0, & x< 0 \end{matrix}\right. \]

3.3 Relu函数代码实现

class ReluActivator(object):

    def Relu(self,x):
        return np.maximum(x,0.0)

    def Relu_derivative(self,x):
        return np.where(x>0,1,0)

    def Relu_gragh(self):
        x = np.arange(-8,8,0.1)
        y = self.Relu(x)
        y_derivative = self.Relu_derivative(x)
        plt.plot(x,y,'g:')
        plt.plot(x,y_derivative,'r-')
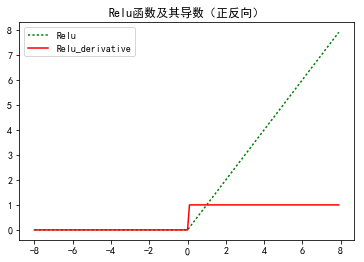
        plt.title("Relu函数及其导数（正反向）")
        plt.legend(['Relu','Relu_derivative'])
        plt.show()

效果图：

if __name__ == '__main__':
    x = 3
    
    #ReLU
    relu = ReluActivator()
    relu.Relu(x)
    relu.Relu_derivative(x)
    relu.Relu_gragh()