PCA原理及代码实现
PCA(Principle Component Analysis)主成分分析是广泛使用的降维算法,由PCA的名字就可以知道,PCA的主要目标是把数据维度降下来,使得减少数据冗余,降低数据处理带来的计算资源消耗。
1 PCA原理
PCA的基本思想是将数据的最主要成分提取出来代替原始数据,也就是将\(n\)维特征映射到,由\(k\)维正交特征组成的特征空间就是主成分,这里使用的降维方法就是投影。问题是怎样抽取数据的主要成分,如何衡量投影后保存的信息呢?PCA算法使用方差来度量信息量,为了确保降维后的低维度数据尽可能多的保留原始数据的有效信息,需要使降维后的数据尽可能的分散,从方差角度理解就是保留最大的方差。那么如何得到包含最大差异性的主成分呢?实际上,计算数据矩阵的协方差矩阵,得到协方差矩阵的特征值和特征向量,然后选择特征值最大的\(k\)个特征对应的特征向量组成的矩阵,就将原始数据矩阵投影到了新的\(k\)维特征空间,实现了数据特征的降维。下面介绍方差和协方差的计算过程,关于特征值和特征向量的计算查看SVD原理。
样本均值:$$\bar{x}=\frac{1}{n}\sum_{i=1}^{n}x_{i}$$
样本方差:$$S{2}=\frac{1}{n-1}\sum_{i=1}\left ( x_{i}-\bar{x} \right )^{2}$$
样本协方差:$$Cov\left ( X,Y \right )=E\left [ \left ( X-E(X) \right ) \left ( Y-E(Y) \right )\right ]=\frac{1}{n-1}\sum_{i=1}^{n}\left ( x_{i} -\bar{x}\right )\left ( y_{i}-\bar{y} \right )$$
2 PCA算法
输入: \(n\)维数据集\(D=\left \{ x^{(1)},x^{(2)},\cdots ,x^{(m)} \right \}\),降维到\(k\)维
输出: 降维后的数据集\({D}'\)
1)对所有的样本数据去中心化:\(x^{(i)}=x^{(i)}-\frac{1}{m}\sum_{j=1}^{m}x^{(j)}\)
2)计算数据集的协方差矩阵\(XX^{T}\)
3)分解协方差矩阵\(XX^{T}\)得到特征值和特征向量
4)取出最大的\(k\)个特征值对象的特征向量\(\left ( w_{1},w_{2},\cdots ,w_{k} \right )\),将所有特征向量标准化得到特征向量矩阵\(W\)
5)对数据集中的每一个样本\(x^{(i)}\),转换为新的样本\(z^{(i)}=W^{T}x^{(i)}\)
6)得到输出样本集\({D}'=\left ( z^{(1)},z^{(2)},\cdots ,z^{(m)} \right )\)
3 PCA代码实现
PCA降维
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.io import loadmat
#2D-->1D
mat = loadmat('D:/Python/Andrew-NG-Meachine-Learning/machine-learning-ex7/ex7/ex7data1.mat')
X = mat['X']
print(X.shape) #(50, 2)
plt.scatter(X[:,0], X[:,1], facecolors='none', edgecolors='b')
#X 均值归一化
def featureNormal(X):
means = X.mean(axis=0)
stds = X.std(axis=0, ddof=1)
X_norm = (X - means)/stds
return X_norm, means, stds
#PCA
def pca(X):
sigma = (X.T@X)/len(X)
U, S, V = np.linalg.svd(sigma)
return U, S, V
X_norm, means, stds = featureNormal(X)
U, S, V = pca(X_norm)
print(U[:,0])
plt.figure(figsize=(7, 5))
plt.scatter(X[:,0], X[:,1], facecolors='none', edgecolors='b')
plt.plot([means[0], means[0]+1.5*S[0]*U[0,0]],
[means[1], means[1]+1.5*S[0]*U[0,1]],
c='r', linewidth=3, label='First Principal Component')
plt.plot([means[0], means[0]+1.5*S[1]*U[1,0]],
[means[1], means[1]+1.5*S[1]*U[1,1]],
c='g', linewidth=3, label='Second Principal Component')
plt.grid()
plt.axis("equal")
plt.legend()
#Dimensionality Reduction with PCA
def projectData(X, U, K):
Z = X @ U[:,:K]
return Z
Z = projectData(X_norm, U, 1)
Z[0]
#print(Z[0]) #[ 1.48127391]
#Reconstructing an approximation of the data 重建数据
def recoverData(Z, U, K):
X_rec = Z @ U[:,:K].T
return X_rec
X_rec = recoverData(Z, U, 1)
X_rec[0]
#print(X_rec[0]) #[-1.04741883 -1.04741883]
#Visualizing the projections
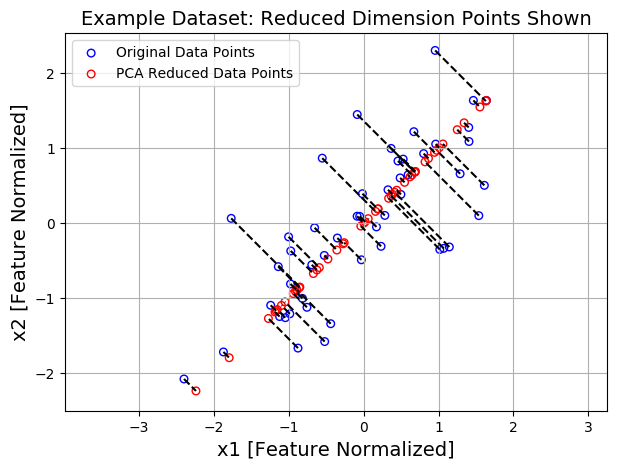
plt.figure(figsize=(7,5))
plt.axis("equal")
plot = plt.scatter(X_norm[:,0], X_norm[:,1], s=30, facecolors='none',
edgecolors='b',label='Original Data Points')
plot = plt.scatter(X_rec[:,0], X_rec[:,1], s=30, facecolors='none',
edgecolors='r',label='PCA Reduced Data Points')
plt.title("Example Dataset: Reduced Dimension Points Shown", fontsize=14)
plt.xlabel('x1 [Feature Normalized]',fontsize=14)
plt.ylabel('x2 [Feature Normalized]', fontsize=14)
plt.grid(True)
for x in range(X_norm.shape[0]):
plt.plot([X_norm[x,0], X_rec[x,0]],[X_norm[x,1], X_rec[x,1]], 'k--')
#输入第一项全是X坐标 第二项全是y坐标
plt.legend()
可视化 PCA将数据从2D减少到1D:


PCA应用 Face Image Dataset 人脸识别图像上运行PCA 实践中使用PCA减少维度
大数据集实现PCA
import numpy as np
import pandas as pd
from scipy.io import loadmat
import matplotlib.pyplot as plt
mat = loadmat('D:/Python/ex7faces.mat')
X = mat['X']
print(X.shape) #(5000, 1024)
def displayData(X, row, col):
fig, axs = plt.subplots(row, col, figsize=(8,8))
for r in range(row):
for c in range(col):
axs[r][c].imshow(X[r*col + c].reshape(32,32).T, cmap = 'Greys_r')
axs[r][c].set_xticks([])
axs[r][c].set_yticks([])
displayData(X, 10, 10)
def featureNormalize(X):
means = X.mean(axis=0)
stds = X.std(axis=0, ddof=1)
X_norm = (X - means) / stds
return X_norm, means, stds
def pca(X):
sigma = (X.T @ X) / len(X)
U, S, V = np.linalg.svd(sigma)
return U, S, V
X_norm, means, stds = featureNormalize(X)
U, S, V = pca(X_norm)
#print(U.shape, S.shape) #(1024, 1024) (1024,)
displayData(U[:,:36].T, 6, 6)
#Dimensionality Reduction
def projectData(X, U, K):
Z = X @ U[:,:K]
return Z
z = projectData(X_norm, U, K=36)
def recoverData(Z, U, K):
X_rec = Z @ U[:,:K].T
return X_rec
X_rec = recoverData(z, U, K=36)
displayData(X_rec, 10, 10)



参考: 吴恩达机器学习



 浙公网安备 33010602011771号
浙公网安备 33010602011771号