RTR-01 Shadow
Shadow Map
- shadow map思路很简洁,就是比较fragment在光照空间中的深度与shadow map记录的最浅深度,来判断是否被遮挡。这是一个比较基础的部分,在这里就不提实现了,感兴趣可以看一下我的OpenGL系列的文章,或者是LearnOpenGL的原文。我实现了三种基本光源的硬阴影(在这里已经用到了PCF),即Dir light、Point light、Spot light。

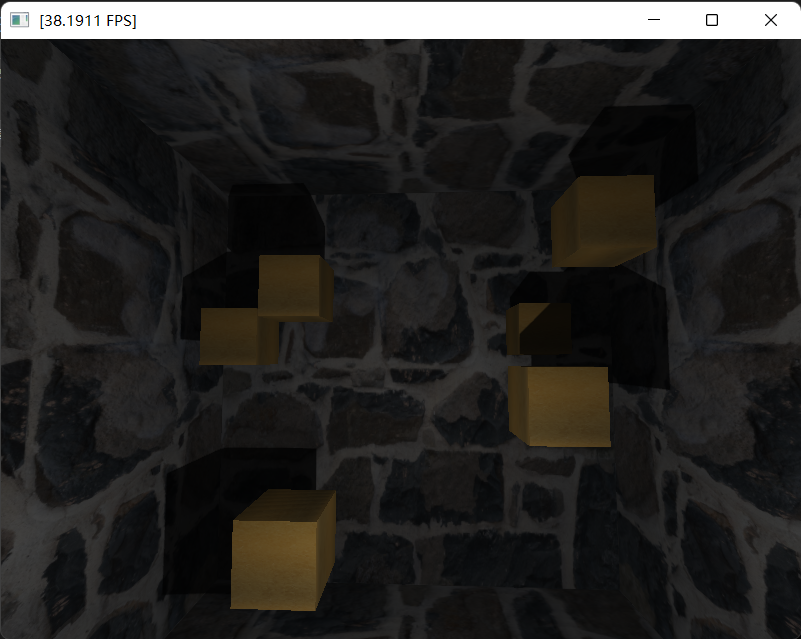
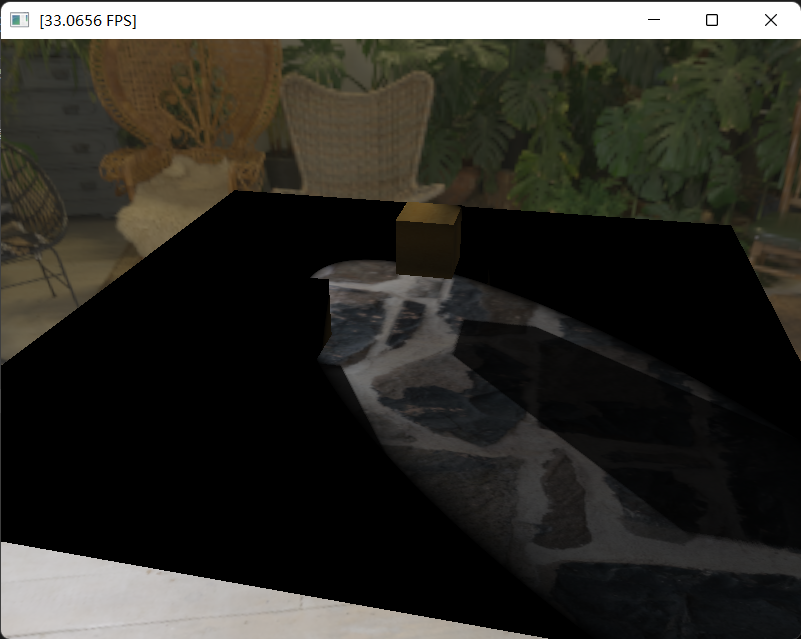
- 比起shadow map的实现,我们在这里更关心它的缺陷。正是由于shadow map的缺陷,发展出了实时阴影的一系列有趣的方法:
- 第一个问题是,阴影失真。这也是大家耳熟能详的一个问题了。阴影失真就是因为,shadow map是一个离散采样得到的纹理,不可避免地就会造成着色点fragment与该点映射到shadow map中对应像素记录的点位置不一致。针对shadow acne,常规的简单方法是设置bias,但是这样会造成Peter Pan,因此,正面剔除来记录背面深度是一个有意思的方法。但是,你也许注意到了,这些方法虽然有效,但是并非一种优雅的解决问题的思路,我们更希望方法本身是优秀的,而非为方法找补。
- 第二个问题是,软阴影。软阴影在光追中是一个不成问题的问题,其问题主要在于采样太少会造成软阴影存在造成,但是实现一个软阴影是光追本身就具备的能力。然而,实时渲染中,shadow map是针对硬阴影的。这个你很容易就可以看出来,因为我们的深度判断是逐片段的。另外,在之前我们也只是实现了点光源、平行光、聚光的shadow map,他们的实现思路也很直观,因为我们很容易地就可以拿到一个光源的观察空间,至于面光源(软阴影的债主),看起来我们似乎找不到一个又能够准确描述面光源阴影深度、又能够保证计算和存储空间优化的shadow map。
- 针对阴影失真的问题,有两个发展路线:其一是直接解决着色点位置不匹配的问题,这个路线有三类主要方法,即不规则z缓冲、光线追踪和体阴影,然而这并不是我们这篇文章的重点,偶们主要关注第二条路线,即滤波。
- 同时,滤波也是软阴影的实现基础。
- 好了,一个简陋而不失雅致的综述就到这里了,下面我们进入正戏,来实现这些方法。
PCF
- PCF是对遮挡进行滤波的一个方法,是一个很直观的简单方法。我们在上面的三个实现就是使用PCF。PCF是一种硬阴影滤波效果很好、滤波原理很直观,并且健壮性很好的一种方法。他既然这么好,我们就不去继续夸夸了,而是找出它的主要问题,这个问题也就是其他的滤波方法的发展基础。即,PCF的滤波是逐fragment的滤波,并不能在shadow map进行滤波,这就使得我们不能使用纹理滤波的方法,比如快速滤波,此外虽然实现了滤波,但却是对离散状态(遮挡)的滤波,所以还是会有比较明显锯齿:

- 因此,其他滤波方法的思路就是,如何在shadow map上实现滤波呢?
VSM
- 你可以把VSM看作PCF的加速方法,也可以看作在shadow map上实现滤波的PCF方法。但是,实际上VSM是一种独立(而且有趣)的阴影滤波方法([10]William Donnelly)。
- VSM的基础是Chebychev’s inequality,对于一个分布\((\mu,\sigma)\),我们可以依此确定CDF的下界,也就是shadow遮挡结果的下界。那么,我们就可以使用切不雪夫不等式来计算遮挡结果的下界值。
- 我们只需要拿到,fragment局部范围内的阴影分布的均值和方差就可以了,其中,方差可以使用均值计算得到:
- 因此,我们维护shadowmap以及shadow^2 map两张图就可以了,但是这样又会造成对采样的需求。所以,实现思路有:Mipmap、Gauss Filter以及SAT。我们这篇文章选择使用SAT。
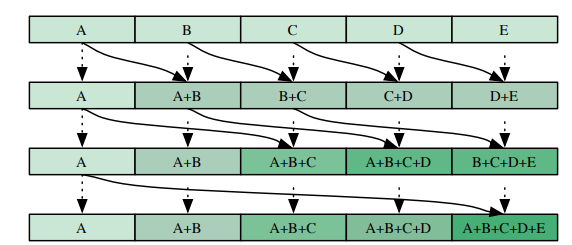
- 但是,SAT的维护也是一件计算量不少的工作,如果逐行遍历,我们就需要\(m\times n\)次计算,幸运的是已经有工作为我们提供了SAT的加速计算方法([2]Justin Hensley),我们只需要\(logm+logn\)次计算就可以实现SAT。这个方法的思路很简单,我们只需要首先逐行计算出SAT,然后逐列计算就可以了,此外每次计算我们的步长都会以r的幂次增长,这样一来就获得了一个适合使用GPU来计算SAT的算法。进一步的,为了减少PASS,可以选取r值不等于2,并且在每次计算中多计算一些和值,注意r值只能选取shadowmap的宽高的整数幂次因子。

这个是行计算的shader。
#version 330 core
in vec2 texCoord;
out vec4 fragColor;
uniform int r;
uniform int index;
uniform sampler2D satMap;
//uniform bool first;
void main()
{
vec2 color = vec2(0.0f);
vec2 texelSize = 1.0 / textureSize(satMap, 0);
for (int i = 0; i != r; i++)
{
vec2 tex = vec2(texCoord.x + i * pow(r, index) * texelSize.x, texCoord.y);
color += texture(satMap, tex).rg;
//color += first ? 1.0 - texture(satMap, tex).rg : texture(satMap, tex).rg;
}
fragColor = vec4(color, 0.0f, 1.0f);
}
这个是对shadow map的SAT,其中分别使用了2、4、32三种r值。
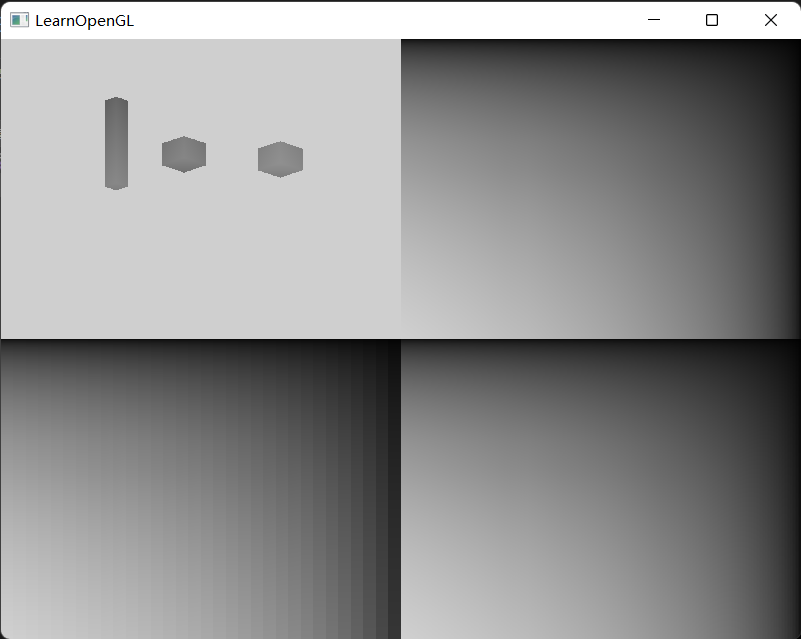
当然,我们需要实现深度以及深度平方两个SAT。
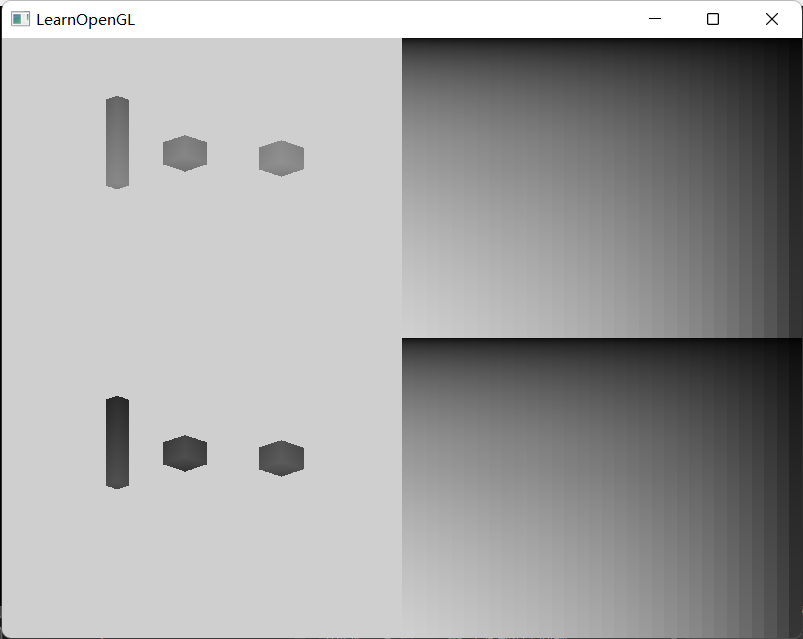
我们对两个SAT做一下差值就可以看出我们确实拿到了一个具有SAT特征的纹理。

- 现在我们已经拿到SAT了,那么计算shadow就是一个自然而然的事情了。

float ShadowCalculation(vec4 fragPosLightSpace, vec3 normal, vec3 lightDir)
{
vec3 projCoord = fragPosLightSpace.xyz / fragPosLightSpace.w;
projCoord = projCoord * 0.5 + 0.5;
float currentDepth = projCoord.z * (1.0 - 0.00003) + 0.5 * 0.00003;
vec2 texelSize = 1.0 / textureSize(satMap, 0);
vec2 left_down = vec2(projCoord.x - kernelSize * texelSize.x, projCoord.y - kernelSize * texelSize.y);
vec2 right_down = vec2(projCoord.x + kernelSize * texelSize.x, projCoord.y - kernelSize * texelSize.y);
vec2 left_up = vec2(projCoord.x - kernelSize * texelSize.x, projCoord.y + kernelSize * texelSize.y);
vec2 right_up = vec2(projCoord.x + kernelSize * texelSize.x, projCoord.y + kernelSize * texelSize.y);
vec2 depthSum = texture(satMap, left_down).rg - texture(satMap, left_up).rg - texture(satMap, right_down).rg + texture(satMap, right_up).rg;
float num = float(4 * kernelSize * kernelSize);
float EX = depthSum.x / num;
float EX2 = depthSum.y / num;
float Var = max(EX2 - EX * EX, 0.001);
float t_EX = currentDepth - EX;
float Pt = (Var + 0.001) / (Var + t_EX * t_EX + 0.001);
//Pt = clamp(Pt, 0.0, 1.0);
Pt = 1.0 - Pt;
//远处
if (projCoord.z > 1.0f || projCoord.x > 1.0f || projCoord.y > 1.0f || projCoord.x < 0.0f || projCoord.y < 0.0f)
Pt = 0.0f;
if (projCoord.z < 0.0f)
Pt = 1.0f;
return Pt;
}
- 有一个问题你也许注意到了,VSM的阴影有点淡,并且在根部阴影都快要消失了。这是因为VSM得到的是遮蔽结果的下界值,并且在诸多的阴影滤波方法中,VSM的shadow遮蔽判断尤其地平缓,因此一来阴影会比较浅,二来在离遮挡物比较近地地方阴影会更浅。
ESM
- ESM是另一种非常巧妙的方法([6]Thomas Annen),他发展自CSM。
- ESM的思路是,PCF是一个二值判断的方法,那么就不能去对其中一个参数做滤波,如果我们将这个过程转换做一个可以将两个参数解耦的计算,那么我们就可以对其中一个参数滤波了。ESM实现这个思路是通过指数函数来解释深度判断。
其中,c是一个比较大的正数,一般取80.0f。
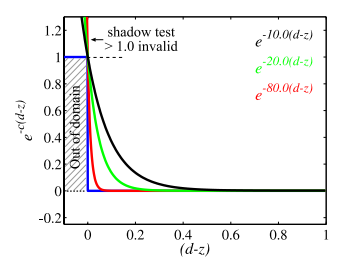
- 那么,我们对遮蔽结果的滤波,可以转换为对深度的指数的滤波,相应的这个深度值的指数被我们保存在ESM中。
- 现在,我们的思路就很清晰了,我们只需要实现一个指数阴影贴图就可以了。

- 接着,我们对ESM做滤波:

- 最后,很自然地就可以计算出来shadow了。可以看出,我们的阴影边缘少了明显的锯齿。

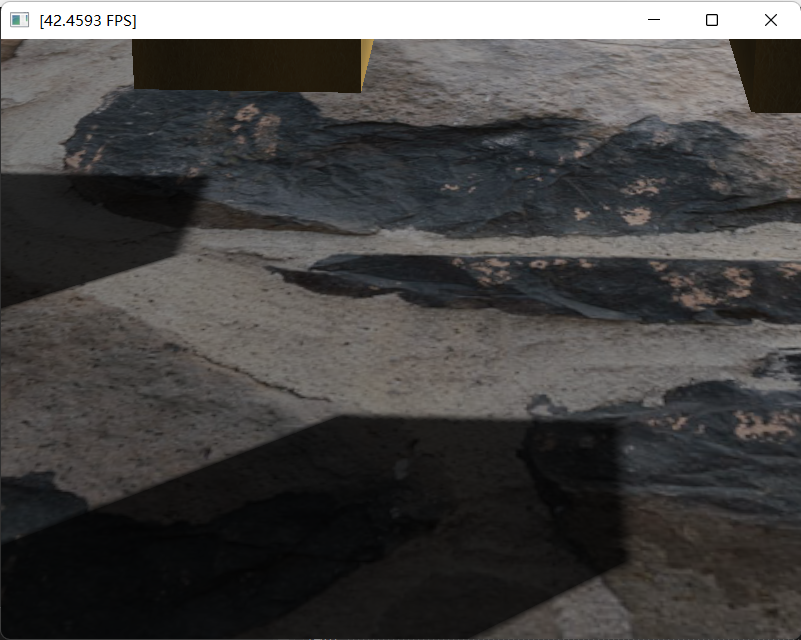
- 同样的,我们可以看出根部的阴影也有些淡,造成这个的原因与VSM是一样的。
float ShadowCalculation(vec4 fragPosLightSpace, vec3 normal, vec3 lightDir)
{
vec3 projCoord = fragPosLightSpace.xyz / fragPosLightSpace.w;
projCoord = projCoord * 0.5 + 0.5;
float closestExpDepth = texture(expMap, projCoord.xy).r;
float currentExpDepth = exp(-c * projCoord.z);
float shadow = 1.0 - currentExpDepth * closestExpDepth;
shadow = clamp(shadow, 0.0, 1.0);
//远处
if (projCoord.z >= 1.0f || projCoord.x >= 1.0f || projCoord.y >= 1.0f || projCoord.x <= 0.0f || projCoord.y <= 0.0f)
shadow = 0.0f;
return shadow;
}
MSM
- 上面的PCF、ESM、VSM都使用了各自的方式来实现滤波的硬阴影。MSM的作者[7]给出了这些方法的一种通用解释,并按照他的这种解释论述了自身的滤波方法,即Moment Shadow Mapping,使用的是矩方法。
- shadow map:
我们使用shadow map来记录深度信息,一般来说我们记录的是z值,这是一个一维的值\(z \in R\)。从之前的VSM中,我们可以看出shadow map不只是可以记录z值,还可以记录其他的信息,比如VSM的\(z^2\),亦即说VSM的shadow map记录了\([z,z^2]\in R^2\)。但是,无论怎样shadow map都是来自z值,因此,我么可以这样描述shadow map,\(b:[0,1]\rightarrow R^m\),在PCF中便是\(b(z):z\)。显然的是,z值本身就包含了关于深度的全部信息,对其进行扩充显然是一种冗余。 - filterable shadow map
对于PCF,它是对深度判断的结果做滤波,这样可以减轻锯齿,也可以缓解acne。不同于PCF,VSM、CSM和ESM都是在shadow map上面做滤波,这样就可以充分利用texture滤波的加速方法。我们期望一种硬阴影方法尽量采取在shadow map上的滤波。 - 启发式方法
我们将根据shadow map的信息\(b(z)\)来判断遮挡的过程看作一次函数计算,\(F_{z_f}(z_f)\)。直接使用shadow map的深度比较,相当于\(F_{z_f}(z_f)=Z(z<z_f)\)。这种方法的一个最致命的问题是,这是一个阶跃函数,非常陡峭,因此就会出现明显的acne问题。对于这个问题,显然我们可以将该函数变得更加平滑就可以了。PCF在深度判断之后做滤波的思路是直观的,也就是对前面的函数结果做滤波。但是,如果我们将shadow map做滤波,然后去做深度判断,显然是一种不明智的做法。因为这只是偏移了阶跃函数的位置,相当于最简单的offset方法。因此,我们遇到的问题是,我们可以实现对shadow map的滤波,但是缺少一个函数来描述深度判断的过程。对于VSM,是使用Chebychev’s inequality来实现估计的;而ESM,则是使用指数近似函数来估计的。一个明显的现象是,这些方法,包括PCF,的深度判断函数都是平滑的,进一步的都是阶跃函数的下界,这个原因正如之前所说的是为了减少acne。但是,就像我们在之前提到的,这些启发式方法都有一个问题,那就是光泄露。这是因为如果函数过于平缓,那么处于相邻位置的shading point如果对应的shadow map处于不同的层深,就会可能有比较大差异的shadow值,这样就会使得阴影本应该比较连续的地方出现了明暗的变化,即light leak。因此,对于一个硬阴影方法,我们不仅期待他是平缓的下界,而且最好是下确界。
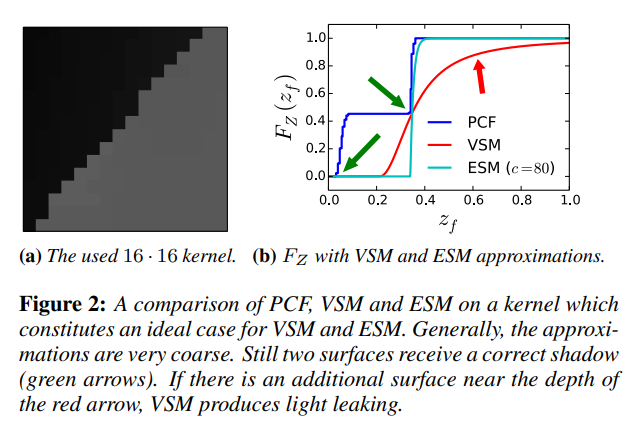
- Moment problem
使用矩(是一种统计中的概念,描述期望及其拓展信息,也即是我们模糊了的深度信息)来获得对值的函数的估计,便是矩问题。在这里,我们期待的是下界的估计。但是,显然的一个问题是,我们不可能期待任意采样的深度z值就看可以获得有效的矩计算过程。

作者给出了一般矩问题计算的算法流程:使用记录的矩信息\(b\)以及采样计算出来的各阶矩信息对应的值\(A\),来最优计算出矩计算的线性参数\(w\),然后我们就可以利用\(w\)来计算深度判断结果\(\delta\)的矩,作为结果。

作者通过尝试,给出了下面的几种矩,一般的使用第一种,称作Hamburger four moment shadow mapping (Hamburger 4MSM),一般简称为MSM。
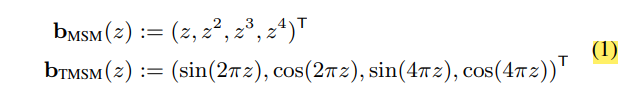
针对深度采样的问题,作者给出了对于Hamburger MSM的评估方法,首先使用记录的矩信息以及shading point的深度值及其各阶矩对应的值,来评估出采样深度,然后利用计算出来的深度值来评估出线性参数\(w\)。

一般的,我们采取四阶Hamburger矩,因此流程可以具体地写作:

- differential entropy
此外,因为这个MSM显然需要记录四张shadow map,并且这些shadow map还需要保证精度,因此其空间问题是该方法一个明显的问题。对于此,作者给出了自己的补救方法,也就是微分熵differential entropy。微分熵可以衡量非均匀分布的值相对于均匀分布的值在存储时丢失的熵值。

我们期待对原来的shadow map做线性变换,使其微分熵尽可能小,可就是差值尽可能大:
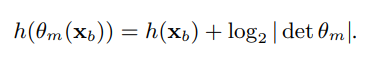
按照这种思路,得到的线性变换是:

- 实现
首先,我们需要获得各阶的矩信息,并对其作模糊,需要注意的是我们在保存矩信息时要使用一次编码来修改微分熵。
#version 330 core
in vec2 texCoord;
out vec4 fragColor;
uniform sampler2D depthMap;
uniform bool horizontal;
uniform int kernelSize;
const float weight[5] = float[](0.227027, 0.1945946, 0.1216216, 0.054054, 0.016216);
uniform bool last;
vec4 Entropy(vec4 moment)
{
vec4 ent = moment;
mat4 Mat = mat4(
-2.07224649, 13.7948857, 0.105877704, 9.79240621,
32.2370378, -59.4683976, -1.90774663, -33.76521106,
-68.5710746, 82.035975, 9.34965551, 47.9456097,
39.3703274, -35.3649032, -6.65434907, -23.9728048);
ent = Mat * ent;
ent.x += 0.0359558848;
return ent;
}
void main()
{
vec2 texOffset = 1.0 / textureSize(depthMap, 0);
float depth = texture(depthMap, texCoord).r;
float depth2 = depth * depth;
vec4 depthVec = vec4(depth, depth2, depth * depth2, depth2 * depth2);
vec4 result = depthVec * weight[0];
float weightTotal = weight[0];
if (horizontal)
{
for (int i = 1; i != kernelSize; i++)
{
depth = texture(depthMap, texCoord + vec2(texOffset.x * i, 0.0)).r;
depth2 = depth * depth;
depthVec = vec4(depth, depth2, depth * depth2, depth2 * depth2);
result += depthVec * weight[i];
depth = texture(depthMap, texCoord - vec2(texOffset.x * i, 0.0)).r;
depth2 = depth * depth;
depthVec = vec4(depth, depth2, depth * depth2, depth2 * depth2);
result += depthVec * weight[i];
weightTotal += 2.0 * weight[i];
}
}
else
{
for (int i = 1; i != kernelSize; i++)
{
depth = texture(depthMap, texCoord + vec2(0.0, texOffset.y * i)).r;
depth2 = depth * depth;
depthVec = vec4(depth, depth2, depth * depth2, depth2 * depth2);
result += depthVec * weight[i];
depth = texture(depthMap, texCoord - vec2(0.0, texOffset.y * i)).r;
depth2 = depth * depth;
depthVec = vec4(depth, depth2, depth * depth2, depth2 * depth2);
result += depthVec * weight[i];
weightTotal += 2.0 * weight[i];
}
}
result /= weightTotal;
fragColor = last ? Entropy(result) : result;
}
然后,我们拿到矩信息之后,首先对其解码,然后利用 Cholesky decomposition求解出c值,接着利用二次方程求解出两个深度采样值,最后利用这两个采样值以及shaing point的深度信息来获得shadow值。
#version 330 core
out vec4 fragColor;
uniform sampler2D momentMap;
const float alpha = 0.00003;
in VS_OUT{
vec3 fragPos;
vec3 normal;
vec2 texCoord;
vec4 fragPosLightSpace;
} fs_in;
uniform vec3 viewPos;
struct Material {
//vec3 ambient;
sampler2D diffuse;
sampler2D specular;
float shininess;
};
uniform Material material;
struct PointLight {
vec3 position;
vec3 ambient;
vec3 diffuse;
vec3 specular;
float constant;
float linear;
float quadratic;
};
uniform PointLight pointlight;
vec3 calcPointLight(PointLight light, vec3 normal, vec3 viewPos, vec3 fragPos);
float ShadowCalculation(vec4 fragPosLightSpace, vec3 normal, vec3 lightDir);
vec4 InvEntropy(vec4 moment);
void main()
{
vec3 result = calcPointLight(pointlight, fs_in.normal, viewPos, fs_in.fragPos);
fragColor = vec4(vec3(result), 1.0f);
}
vec3 calcPointLight(PointLight light, vec3 normal, vec3 viewPos, vec3 fragPos)
{
float distance = length(light.position - fragPos);
float attenuation = 1.0f / (light.constant + light.linear * distance + light.quadratic * distance * distance);
//ambient
vec3 ambient = light.ambient * vec3(texture(material.diffuse, fs_in.texCoord));
//diffuse
vec3 lightDir = normalize(light.position - fragPos);
float diff = max(dot(normal, lightDir), 0.0);
vec3 diffuse = light.diffuse * diff * vec3(texture(material.diffuse, fs_in.texCoord));
//specular
vec3 viewDir = normalize(viewPos - fragPos);
vec3 halfwayDir = normalize(viewDir + lightDir);
float spec = pow(max(dot(halfwayDir, normal), 0.0), material.shininess);
vec3 specular = light.specular * spec * vec3(texture(material.specular, fs_in.texCoord));
float shadow = ShadowCalculation(fs_in.fragPosLightSpace, normal, lightDir);
return (ambient + (1.0 - shadow) * (diffuse + specular))* attenuation;
}
float ShadowCalculation(vec4 fragPosLightSpace, vec3 normal, vec3 lightDir)
{
vec3 projCoord = fragPosLightSpace.xyz / fragPosLightSpace.w;
projCoord = projCoord * 0.5 + 0.5;
float zf = projCoord.z;
float bias = 0.0;
zf -= bias;
//b
vec4 b = InvEntropy(texture(momentMap, projCoord.xy));
b = mix(b, vec4(0.5, 0.5, 0.5, 0.5), alpha);
//L
float L11 = 1.0;
float L21 = b.x;
float L22 = sqrt(b.y - L21 * L21);
float L31 = b.y;
float L32 = (b.z - L21 * L31) / L22;
float L33 = sqrt(b.w - L31 * L31 - L32 * L32);
//c
vec3 c;
c.x = 1.0;
c.y = (zf - L21 * c.x) / L22;
c.z = (zf * zf - L31 * c.x - L32 * c.y) / L33;
c.z = c.z / L33;
c.y = (c.y - L32 * c.z) / L22;
c.x = (c.x - L21 * c.y - L31 * c.z) / L11;
//z2 z3
float delta = sqrt(c.y * c.y - 4 * c.x * c.z);
float z2 = clamp((-c.y - delta) / (2.0 * c.z), 0.0, 1.0);
float z3 = clamp((-c.y + delta) / (2.0 * c.z), 0.0, 1.0);
if (z3 < z2)
{
float zint = z3;
z3 = z2;
z2 = zint;
}
//G
vec4 pars;
if (zf <= z2)
pars = vec4(0.0, 0.0, 0.0, 0.0);
else if (zf <= z3)
pars = vec4(zf, z2, 0.0, 1.0);
else
pars = vec4(z2, zf, 1.0, 1.0);
float G = pars.z + pars.w * (pars.x * z3 - b.x * (pars.x + z3) + b.y) / ((zf - z2) * (z3 - pars.y));
G = clamp(G, 0.0, 1.0);
float shadow = G;
//if (projCoord.z >= 1.0f || projCoord.x >= 1.0f || projCoord.y >= 1.0f || projCoord.x <= 0.0f || projCoord.y <= 0.0f)
// shadow = 0.0f;
return shadow;
}
vec4 InvEntropy(vec4 moment)
{
vec4 inv = moment;
inv.x -= 0.0359558848;
mat4 invMat = mat4(
0.222774414, 0.154967927, 0.145198897, 0.163127446,
0.0771972849, 0.139462944, 0.212020218, 0.259143230,
0.792698661, 0.796341590, 0.725869459, 0.653909266,
0.0319417572, -0.172282318, -0.275801483, -0.337613176);
inv = invMat * inv;
return inv;
}
这是前两阶矩的滤波前后结果。

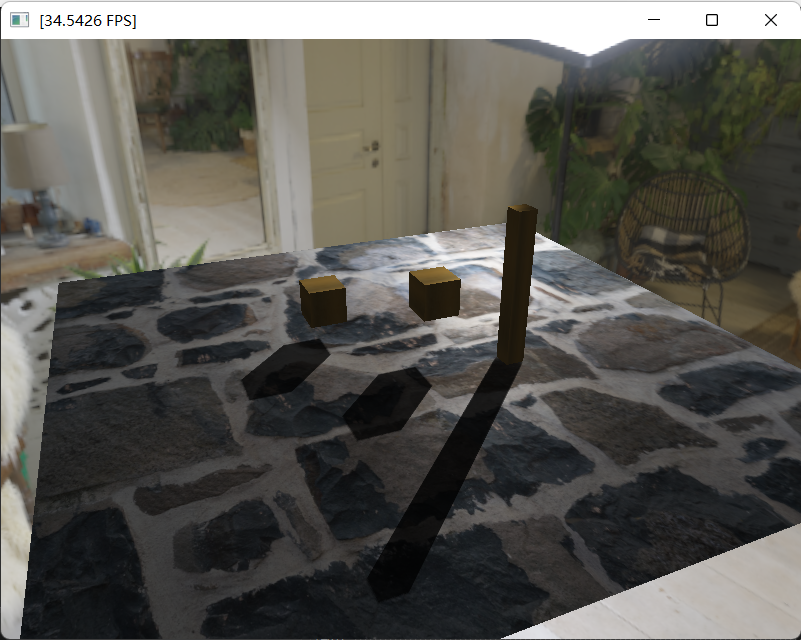
这是最终效果,可见这个硬阴影非常好!
PCSS
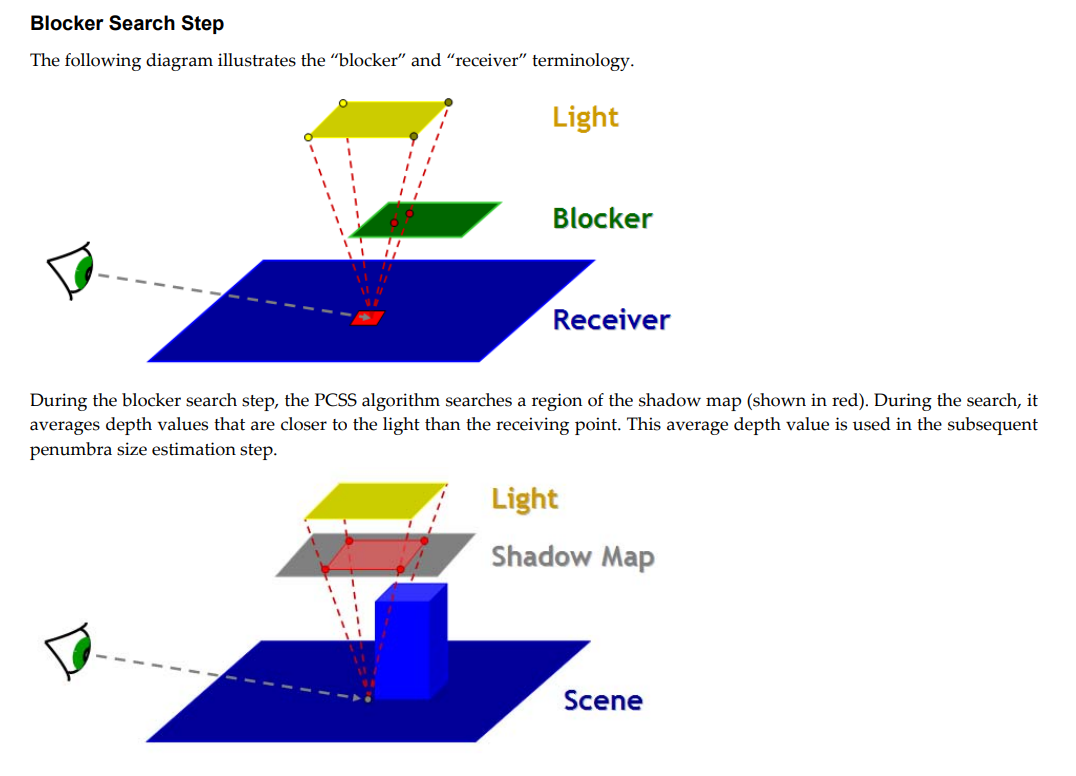
- 好了,经典的硬阴影方法已经在上面了,下面我们谈一下软阴影。首先,说一下PCSS[1]。
- 从PCF中可以看出,如果我们取滤波的范围越大,那么阴影边缘就会越软。那么,PCSS就利用了这个规律,通过调整滤波的核的尺寸来调整软硬。
- PCSS是一个two pass方法。首要的是,我们需要计算出滤波核的尺寸,这需要拿到遮挡物深度\(d_{Blocker}\)、着色点深度\(d_{Receiver}\)以及面光源的尺寸\(w_{light}\)。
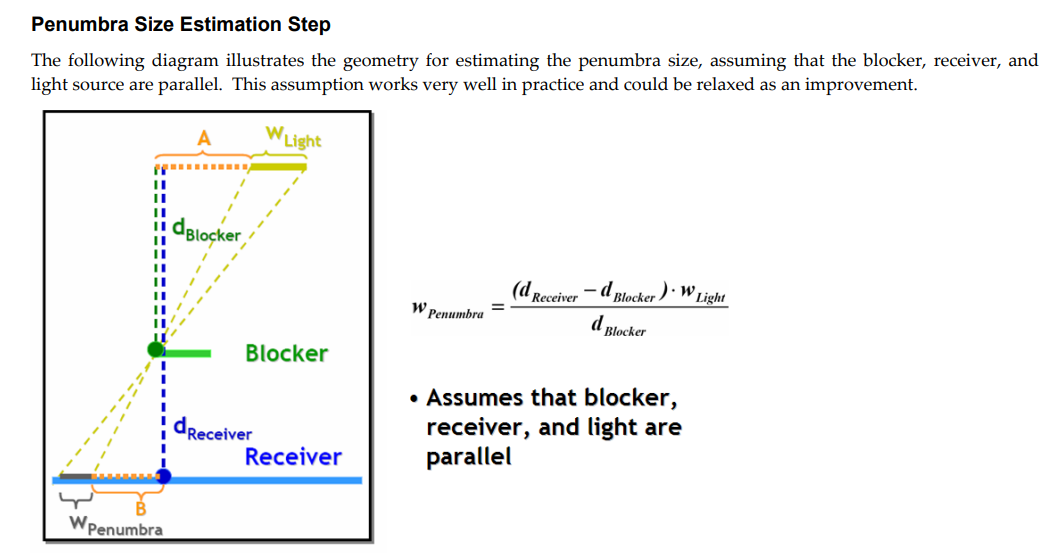
- 进一步的,我们要计算滤波核尺寸,就要首先拿到遮挡物深度\(d_{Blocker}\),这个值是所有遮挡物的平均深度。如果要计算精确的值,就需要对shadow map做采样,那么计算量就会很大。因此,这里才取得是估计的方法,首先确定采样的范围,然后对范围内的进行采样,这个采样范围是通过面光源尺寸和shadow map的尺寸来获得的对shadow map的采样范围的,这是一种简化的方法。
float ShadowCalculation(vec4 fragPosLightSpace, vec3 normal, vec3 lightDir)
{
vec3 projCoord = fragPosLightSpace.xyz / fragPosLightSpace.w;
projCoord = projCoord * 0.5 + 0.5;
float closestDepth = texture(shadowMap, projCoord.xy).r;
float currentDepth = projCoord.z;
float shadow = 0.0f;
float bias = 0.0;// max(0.05 * (1.0 - dot(normal, lightDir)), 0.005);
//PCSS
float dBlocker = BlockDepth(projCoord.xy, currentDepth);
float dReceiver = currentDepth;
float searchWidth = SearchWidth(dReceiver, dBlocker);
vec2 texelSize = 1.0 / textureSize(shadowMap, 0);
int searchStep = max(int(searchWidth / texelSize.x), 2);
int count = 0;
//PCF
for (int i = -searchStep/2; i != searchStep/2; i++)
{
for (int j = 0; j != searchStep; j++)
{
float pcfDepth = texture(shadowMap, projCoord.xy + vec2(i, j) * texelSize).r;
shadow += currentDepth - bias > pcfDepth ? 1.0 : 0.0;
count++;
}
}
shadow /= float(count);
//远处
if (projCoord.z > 1.0f)
shadow = 0.0f;
if (projCoord.z < 0.0f)
shadow = 1.0f;
return shadow;
}
float BlockDepth(vec2 projCoord, float currentDepth)
{
float ratio = lightWidth / (2.0 * orthoWidth);
float blockDepth = 0.0;
int num = 0;
for (int i = -3; i != 4; i++)
{
for (int j = -3; j != 4; j++)
{
vec2 offset = vec2(i / 6.0 * ratio, j / 6.0 * ratio);
float depth = texture(shadowMap, projCoord + offset).r;
if (depth < currentDepth)
{
blockDepth += depth;
num++;
}
}
}
return num == 0 ? currentDepth : blockDepth / float(num);
}
float SearchWidth(float dReceiver,float dBlocker)
{
dReceiver = dReceiver * (far_plane - near_plane) + near_plane;
dBlocker = dBlocker * (far_plane - near_plane) + near_plane;
float width = (dReceiver - dBlocker) * lightWidth / dBlocker;
width /= orthoWidth;
return width;
}
效果如下:
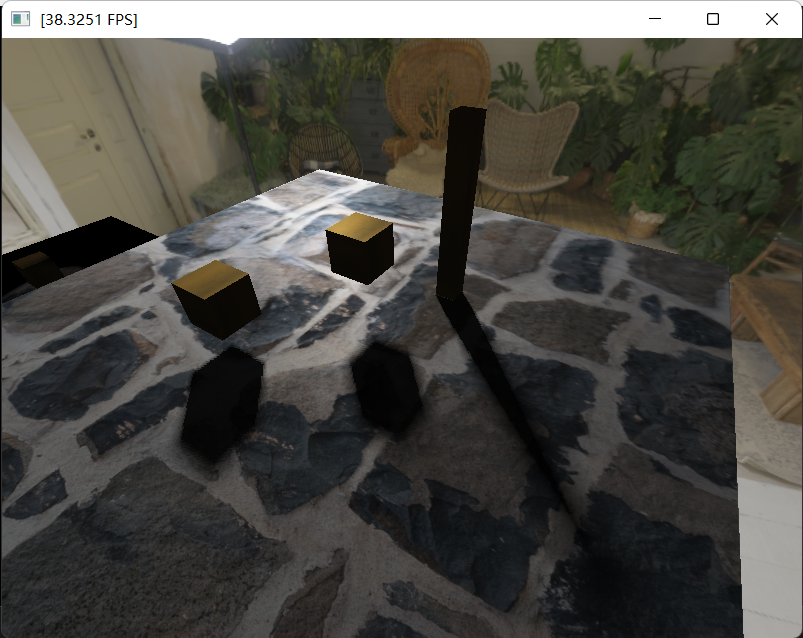
对比一张真实场景中的软阴影,可以看出效果不错:

VSSM
- VSSM的思路与VSM相似。只不过是将PCSS中的PCF过程换做VSM方法。第一个需要换的是,在拿到核宽度之后,直接使用VSM方法获得对深度判断的结果,作为软阴影的shadow值;另一个就是,在拿到blocker depth估计的采样宽度之后,同样的使用VSM方法来评估平均深度。
float ShadowCalculation(vec4 fragPosLightSpace, vec3 normal, vec3 lightDir)
{
vec3 projCoord = fragPosLightSpace.xyz / fragPosLightSpace.w;
projCoord = projCoord * 0.5 + 0.5;
float currentDepth = projCoord.z;
float dBlocker = BlockDepth(projCoord.xy, currentDepth);
float dReceiver = currentDepth;
float searchWidth = SearchWidth(dReceiver, dBlocker);
searchWidth /= 2.0;
vec2 texelSize = 1.0 / textureSize(satMap, 0);
searchWidth = max(searchWidth, 3.0*texelSize.x);
vec2 left_down = vec2(projCoord.x - searchWidth, projCoord.y - searchWidth);
vec2 right_down = vec2(projCoord.x + searchWidth, projCoord.y - searchWidth);
vec2 left_up = vec2(projCoord.x - searchWidth, projCoord.y + searchWidth);
vec2 right_up = vec2(projCoord.x + searchWidth, projCoord.y + searchWidth);
vec2 depthSum = texture(satMap, left_down).rg - texture(satMap, left_up).rg - texture(satMap, right_down).rg + texture(satMap, right_up).rg;
float singleNum = (searchWidth / texelSize.x) * (searchWidth / texelSize.y);
float num = singleNum < 1.0 ? 1.0 : 4.0 * singleNum;
float EX = depthSum.x / num;
float EX2 = depthSum.y / num;
float Var = EX2 - EX * EX;
float bias = 0.005;
float t_EX = currentDepth - EX;
float Pt = (Var+0.001) / (Var + t_EX * t_EX+0.001);
Pt = 1.0 - Pt;
//远处
if (projCoord.z > 1.0f || projCoord.x > 1.0f || projCoord.y > 1.0f || projCoord.x < 0.0f || projCoord.y < 0.0f)
Pt = 0.0f;
if (projCoord.z < 0.0f)
Pt = 1.0f;
return Pt;
}
float BlockDepth(vec2 projCoord, float currentDepth)
{
float winWidth = 0.5 * lightWidth / orthoWidth;
vec2 left_down = vec2(projCoord.x - winWidth, projCoord.y - winWidth);
vec2 right_down = vec2(projCoord.x + winWidth, projCoord.y - winWidth);
vec2 left_up = vec2(projCoord.x - winWidth, projCoord.y + winWidth);
vec2 right_up = vec2(projCoord.x + winWidth, projCoord.y + winWidth);
vec2 depthSum = texture(satMap, left_down).rg - texture(satMap, left_up).rg - texture(satMap, right_down).rg + texture(satMap, right_up).rg;
vec2 texelSize = 1.0 / textureSize(satMap, 0);
float singleNum = (winWidth / texelSize.x) * (winWidth / texelSize.y);
float num = singleNum < 1.0 ? 1.0 : 4.0 * singleNum;
float EX = depthSum.x / num;
float EX2 = depthSum.y / num;
float Var = max(EX2 - EX * EX, 0.001);
float t_EX = currentDepth - EX;
float Pt = (Var+0.001) / (Var + t_EX * t_EX+0.001);
float blockDepth = (EX - Pt * currentDepth) / (1.0 - Pt+0.001);
//平面
if (Pt > 0.95)
blockDepth = currentDepth*0.99;
return blockDepth;
}
float SearchWidth(float dReceiver, float dBlocker)
{
dReceiver = dReceiver * (far_plane - near_plane) + near_plane;
dBlocker = dBlocker * (far_plane - near_plane) + near_plane;
float width = (dReceiver - dBlocker) * lightWidth / (dBlocker);
width /= orthoWidth;
return width;
}
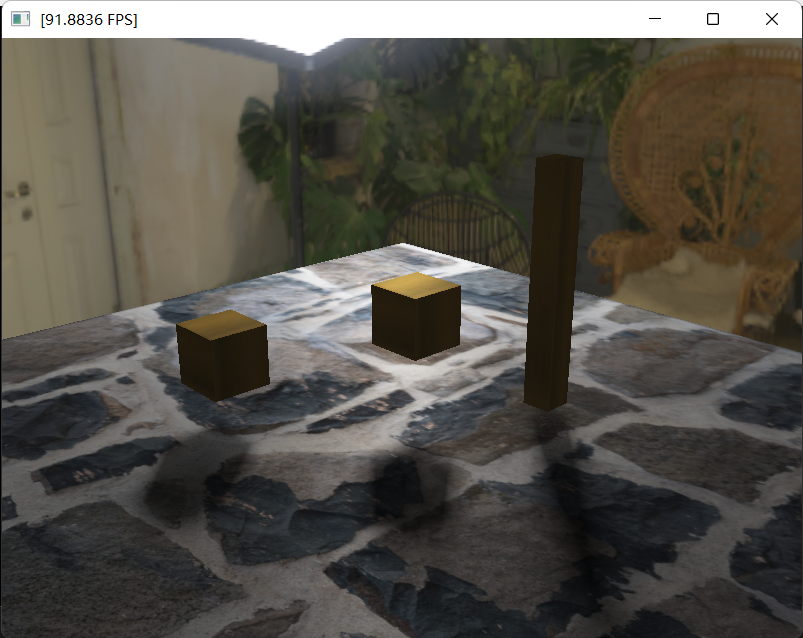
效果如下,很明显的是,与VSM相同,阴影也会很淡。
参考
[1]Randima, Fernando. Percentage-Closer Soft Shadows
[2]Justin Hensley. Fast Summed-Area Table Generation and its Applications
[3]Jon Story, Chris Wyman. HFTS: Hybrid Frustum-Traced Shadows in “The Division”
[4]Johnson. The Irregular Z-Buffer: Hardware Acceleration for Irregular Data Structures
[5]Chris Wyman. Frustum-Traced Raster Shadows: Revisiting Irregular Z-Buffers
[6]Thomas Annen. Exponential Shadow Maps
[7]Christoph Peters. Moment Shadow Mapping
[8]Á Tari. Moments based bounds in stochastic models
[9]COVER, T. M., AND THOMAS, J. A. Elements of Information Theory
[10]William Donnelly. Variance Shadow Maps
本文来自博客园,作者:ETHERovo,转载请注明原文链接:https://www.cnblogs.com/etherovo/p/17446390.html


 浙公网安备 33010602011771号
浙公网安备 33010602011771号