13 Ray Tracing(Whitted-Style Ray Tracing)

关键点

• Shading Mapping
• Recursive Ray Tracing(Whitted-style)
• Ray-Surface Intersection(Implicit Surface)
• Ray-Surface Intersection(Triangle Mesh -- Moller Trumbore Algorithm)
• Accelerating Ray-Surface Intersection(Bounding Volumes：Uniform box -> KD Tree -> BVH)

1. Shadow Mapping

1.1 步骤

• Render from Light
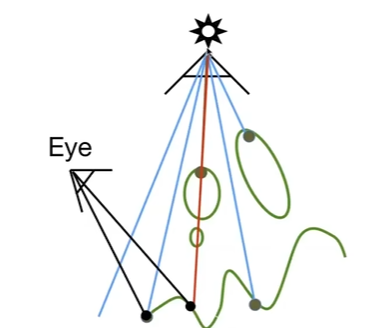
  从光源看向场景，做光栅化，记录能看到的点的深度，得到从光源出发的深度图。
• Project to Light
  从摄像机看向场景，做光栅化，将其中的点投影会光源深度图上，得到光源深度图上的对应像素的深度，此外计算出实际深度，如果深度一致，则该点可以同时被光源和摄像机看到；否则，如果深度不一致，则该点被其他点挡住，不能被摄像机看到。
  

1.2 问题

• 因为深度记录是浮点数，难以判断相等。因此，判断大小，即实际距离大于深度图距离被判定为阴影。但是仍然存在很接近的深度，所以在深度图深度上增加一个bias来比较大小。当然，这些都不能本质上解决问题。
  
• 此外，shadow map具有分辨率，如果其分辨率很低，那么阴影信息是走样的，会形成锯齿阴影。
• 需要渲染两遍，开销很大。
• 只能处理点光源的硬阴影(因为点光源没有大小，所以点要么在阴影中，要么不在，如果是有大小的光源，那么不同光源位置的阴影不同，其综合效果即软阴影)。
  

2. 光线追踪

2.1 光栅化与光线追踪

2.1.1光栅化

缺点

• 光栅化只能处理点光源的硬阴影。
  
• 光栅化不能解决Glossy Reflection，即光线经过两次反射入眼。
  
• 光栅化不能解决Indirection illumination间接光照，即光线多次弹射。
  

优点

• 生成速度快

2.1.2 光线追踪

缺点

• 速度慢，应用于离线处理。

优点

• 高质量

2.2 Light Rays

2.2.1 定义

• 沿直线传播
• 不会碰撞
• 从光源发出，经过若干次反射，进入眼睛；因此光线具有可逆性Reciprocity。
  

2.3 Ray Casting

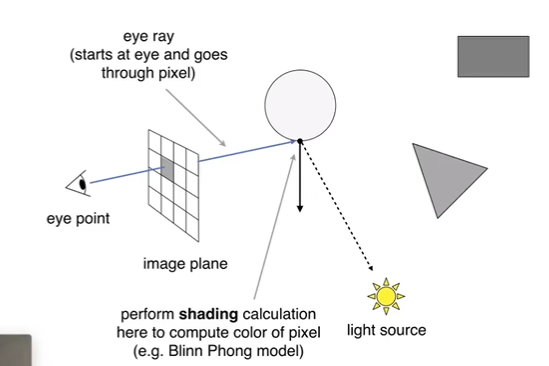
假设光源是点光源，眼睛是一个点，光线会完整反射。从眼镜透过像素发出光线eye ray打到场景中最近的一个物体，记录最近的交点。从该点向光源发出一条光线，如果中间没有物体阻挡，那么光源可知照亮该点，否则在阴影里。在得到两个光线后，结合法线，那么可以进行着色。

2.4 Recursive Ray Tracing(Whitted-style)

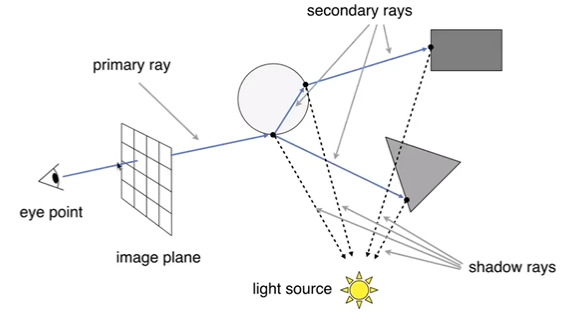
所有从眼睛发出的光线primary ray在打到点上后，进行折射与反射得到secondary ray，再次打到其他点上，最后所有点都与光源做连线shadow ray判断是否被照亮。将所有可被照亮的点的光路的着色结果都加起来。

3. Ray-Surface Intersection

3.1 Ray Equation

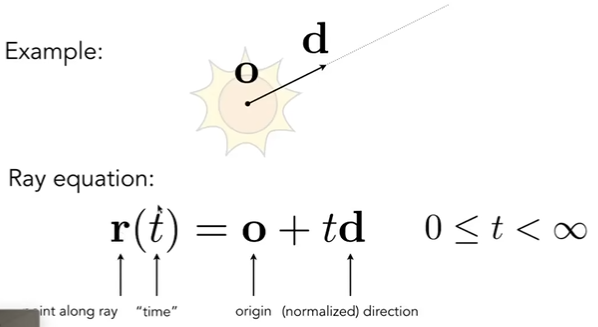
光线由起点与方向定义，光线上的任意一点可以使用起点与方向表示。

3.2 Ray Intersection With Sphere

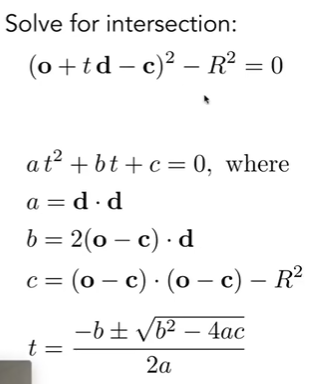
3.2 Ray Intersection With Implicit Surface

3.3 Ray Intersection With Triangle Mesh

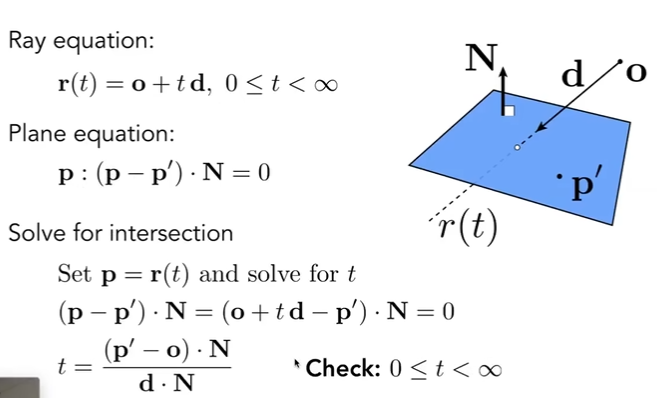
3.3.1 直接思路

将光线与三角形求交点。将光线与平面求交点，然后判断交点是否在三角形内部。其中后者可用叉积得到。通过给定平面上的一个点以及该平面的法线来定义该平面，即平面内的任意一点与给定点的连线与法线垂直(内积为零)，相应的可以写作平面方程。然后利用光线与隐式网格的相交检测方法得到结果。

3.3.2 Moller Trumbore Algorithm

使用重心坐标表示三角形平面内的点，形成线性方程组。可以一步得出光线与平面交点。然后判断结论是否合理：b1、b2、t非负（前两者判断在三角形内部，后者是因为光线是射线）。

4. Accelerating Ray-Surface Intersection --Bounding Volumes 包围盒

在三角形表面显式几何中，需要对每一个三角形求解是否相交，需要加速。用某种简单的几何将物体给包围起来，先检测包围盒与光线是否相交，再判断内部物体。

4.1 Ray-Intersection With Axis-Aligned Box

4.1.1 Axis-Aligned Box

长方体是由三个不同的对面slabs形成的交集。通常使用Axis-Aligned Bounding Box(AABB)轴对齐包围盒，即每一对对面都是平行于一个坐标轴面的。

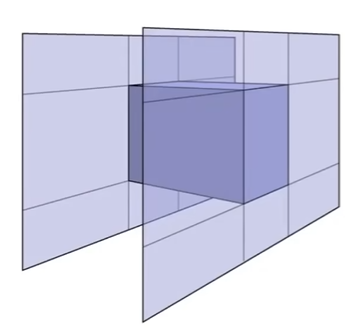
4.1.2 判断条件

以二维为例，分别对两对对面求其进入与出去的时间tmin与tmax，对所有tmin求出最大值即为进入时间，tmax最小值即为出去时间。如果进入时间小于出去时间，那么意味着有一个时间段光线同时处于两对对面的内部，即在盒子内部。

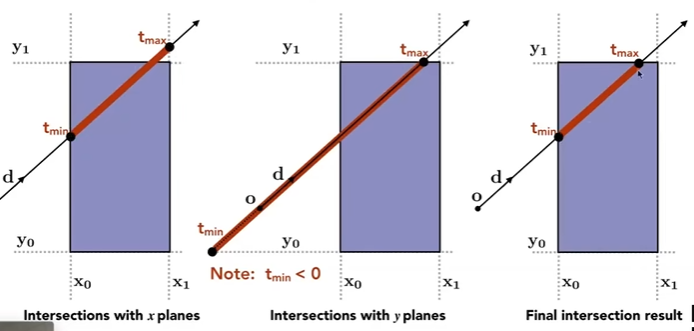
同理，对于3D情况：

• 求三个对面的tmin、tmax；
• 对tmin取最大值为进入时间，对tmax取最小值为出去时间
• 如果tenter<texit则光线进入盒子(直线)
  
• 如果texit<0，则光源在盒子背面，即反向入射盒子，所以没有与盒子相交
• 如果texit>=0 and tenter<0，则光源在盒子内部
  总之，光线进入盒子的条件为：
  tenter<texit && texit>0

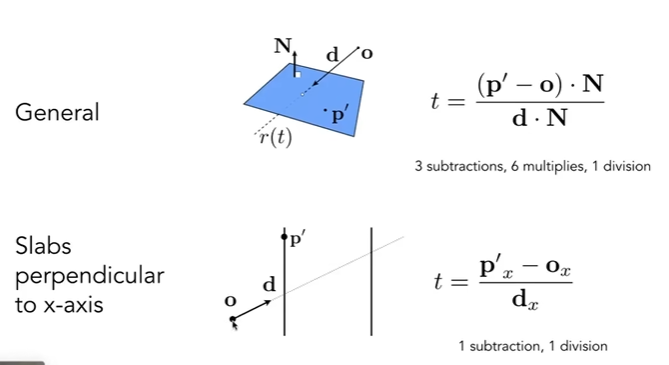
4.1.3 计算

使用轴向盒子，可以简化计算过程：

4.2 Uniform Grid

4.2.1 Preprocess 预处理

• 找到包围盒
• 对包围盒划分格子Grid
• 找到与物体表面相交的格子
  

4.2.2Ray-Scene Intersection

• 光线与格子求交，当找到内部有物体的格子时，进行光线与格子内部的物体的相交判断，如果相交则找到一个交点。
• 判断光线与格子的相交，通过光栅化一条线实现。
  
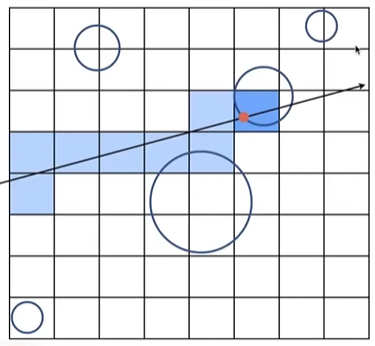
• 在实际中格子的数量是27乘以场景中物体的数量，这是一种尝试的结果来trade off。

4.2.3 缺点

uniform grid方法需要太多的格子，比如在一个大场景中判断一个小的物体。

4.3 Spatial Partitions 空间划分

4.3.1 三种方法

按照空间中物体分布的集中程度来划分格子。

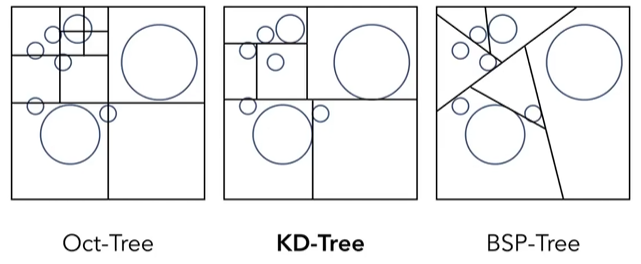
• Oct-tree 八叉树
  将一个AABB划分成八分(3D)，然后对每份继续八分，直到某个格子内部有足够少的物理就停止它的划分。但是其划分格子数与维度成指数关系。
• KD-tree(三种选择中最优)
  每次沿着一个维度切分格子，每次划分的维度交替进行(比如x->y->z)来保证基本是一个近似的方形格子，保障二叉树性质。
• BSP-Tree
  每次选择一个方向切分格子，但是不再轴向，而且每次切分都需要一个超平面，没有轴向超平面计算简单。
  

4.3.2 KD-Tree

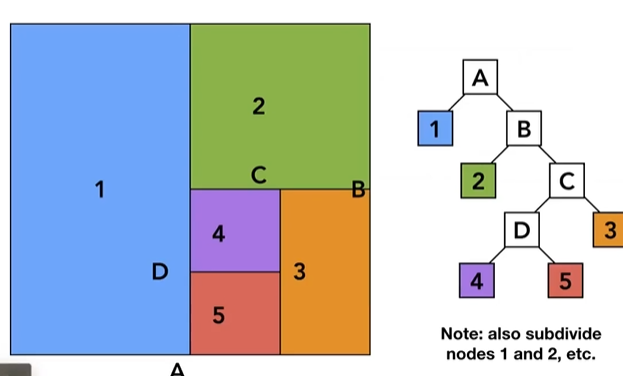
(1) KD-tree的数据结构

• 每个节点保存切分方向和切分位置，以及子节点
• 在叶子节点中保存物体
  

(2) Traversing a KD tree

先判断光线与包围的是否有交点，如果有则判断其与所有子节点是否相交，对于相交的子节点，不断判断相应子节点，直到找到所有的相交的叶子节点，对于找出的叶子节点判断其内部所有物体的交点。

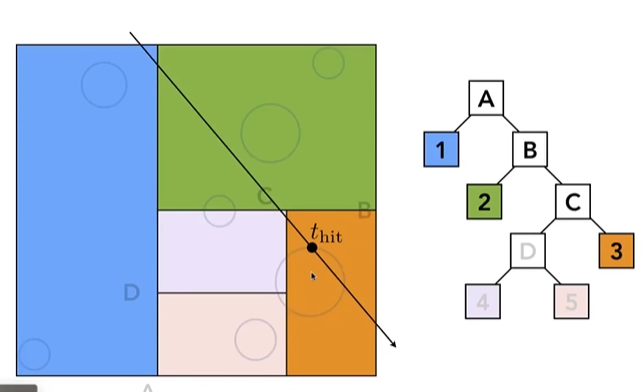
(3) 问题

• 需要判断三角形与AABB的相交关系。
• 此外一个物体可能会被存在不同的格子里面。

4.4 Object Partitions 物体划分 -- Bounding Volume Hierarchy(BVH)

4.4.1 步骤

按照物体划分网格。将空间中的物体分成两个部分，然后重新计算每个包围盒，如此递归直到包围盒中有足够少的三角形。此外，可以按照KD Tree的思想，按照不同方向交替划分物体来保证格子形状。如此避免了KD Tree的两个问题，但是其boundging box存在相交，比较好的划分方法应当尽可能减少box重叠部分。当场景中的物体改变位置后，需要重新计算。

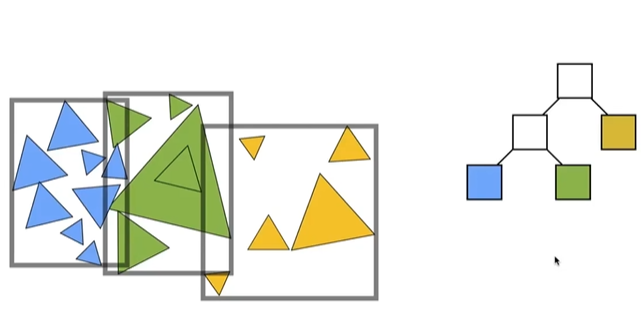
4.4.2 技巧

• 为了让三角形在空间中均匀分布，每次划分box的最长的轴是一个挺好的选择，比如box是一个长条形。
• 可以按照位于中间位置的三角形的位置来划分位置，可以保证两边box的三角形数量，可以保证tree比较平衡，即减少最大深度。可以按照三角形重心在某个轴方向上排序，但是事实上不需要排序，使用快速选择算法O(N)。

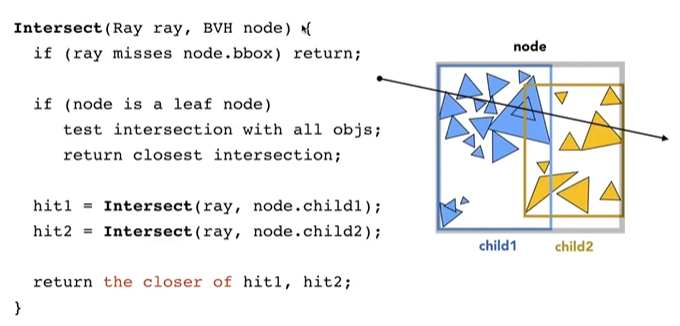
4.4.3 BVH Traversal

类似于KD-Tree，先判断AABB，如果相交且是中间节点，则递归求解子节点，直到找到相交的叶子节点，再判断内部三角形。

来源

[1]Games101. 闫令琪