04 Viewing Transformation
关键点
- ModelView Transformation Matrix (1-3)
- Orthographic Projection Matrix (4)
- Perspective Projection Matrix (5-6)
1. View/Camera/ModelView Transformation
- MVP(model transformation -> view transformation -> projection transformation)
- Camera define (Position e, look at/gaze direction g, up direction t)
- 考虑到相机拍摄结果是相机与物体的相对结果,所以固定相机与固定物品效果一样,固定标准如下:
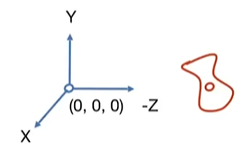

- 将相机运行(e,g,t)变换到相机固定(0,-z,y)
首先进行平移,(xe,ye,ze)到原点(0,0,0):
\[T_{view}=
\left[
\begin{matrix}
1 & 0 & 0 & -x_e \\
0 & 1 & 0 & -y_e \\
0 & 0 & 1 & -z_e\\
0 & 0 & 0 & 1 \\
\end{matrix} \right]\tag{1}
\]
然后进行旋转,g->-Z, t->Y, gxt->X,直接求解旋转矩阵比较复杂,所以求其逆矩阵(-g<-Z, t<-Y, gxt<-X),可以直接由g与t的向量表示得到,同时考虑到旋转矩阵的逆矩阵是其转置,得到旋转矩阵:

\[R_{view}=
\left[
\begin{matrix}
x_{\vec{g}\times\vec{t}} & y_{\vec{g}\times\vec{t}} & z_{\vec{g}\times\vec{t}} & 0 \\
x_t & y_t & z_t & 0 \\
x_{-g} & y_{-g} & z_{-g} & 0\\
0 & 0 & 0 & 1 \\
\end{matrix} \right]\tag{2}
\]
得到视图变换矩阵:
\[M_{view}=R_{view}T_{view}\tag{3}
\]
视图变换矩阵是世界固定坐标系(物理意义直观)向相机固定坐标系(便于投影)转换的变换矩阵,在相机运动坐标系下可以通过相机位置得到视图变换矩阵,通过该矩阵可以得到所有物体在相机固定坐标系下的位置。
2. Projection Transformation
- Orthographic projection 正交投影 and Perspective projection 透视投影
比起正交投影,透视投影可以造成近大远小的效果。
对于透视投影,入射光线是锥形;对于正交投影,入射光线是平行的,即相机无限远。
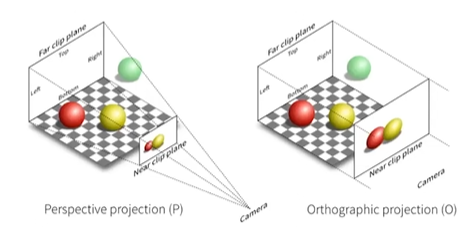
2.1 Orthographic projection
对空间中某一个立方体空间作正交投影:
- 定义一个空间立方体,即定义左右下上远近的六个位置[l,r]x[b,t]x[f,n](分别为xyz坐标,其中left<right,bottom<top,far<near(因为-z),符合右手);然后映射到标准立方体[-1,1]^3(先平移中心到原点,再缩放)。

- 变换矩阵如下:
\[M_{ortho}=
\left[
\begin{matrix}
\frac{2}{r-l} & 0 & 0 & 0 \\
0 & \frac{2}{t-b} & 0 & 0 \\
0 & 0 & \frac{2}{n-f} & 0\\
0 & 0 & 0 & 1 \\
\end{matrix}\right]
\left[\begin{matrix}
1 & 0 & 0 & -\frac{l+r}{2} \\
0 & 1 & 0 & -\frac{b+t}{2} \\
0 & 0 & 1 & -\frac{f+n}{2}\\
0 & 0 & 0 & 1 \\
\end{matrix} \right]\tag{4}
\]
2.2 Perspective projection
2.2.1 投影
规定近平面不变、远平原z轴位置不变、远平面中心位置不变,压缩远平面,然后进行正交投影。
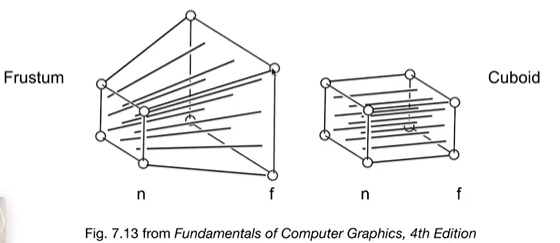
首先进行压缩:


由齐次坐标中点的一致形式,将压缩结果中的各个已知维度表达为原坐标的乘积形式:

那么,就可以使用矩阵变换来表示:
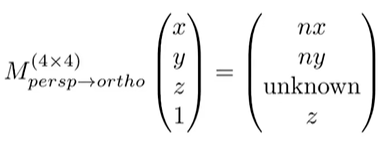
相应的变换矩阵为:
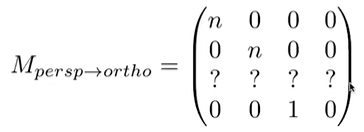
同时,考虑到z坐标的映射等于自身(不是坐标一样,而是表示齐次坐标下的同一z轴位置),可以得到近平面的关系:
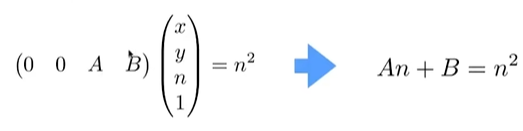
此外,由于中心点映射自身,得到远平面:

可得:

最终得到:
\[M_{persp->ortho}=
\left[
\begin{matrix}
n & 0 & 0 & 0 \\
0 & n & 0 & 0 \\
0 & 0 & n+f & -nf\\
0 & 0 & 1 & 0 \\
\end{matrix} \right]\tag{5}
\]
\[M_{persp}=M_{ortho}M_{persp->ortho}\tag{6}
\]
2.2.2 视锥
- Aspect Ratio 宽高比
- Vertical Field of view (fovY) 垂直可视角度
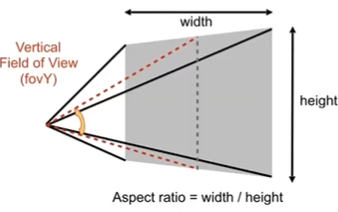
在视锥的定义中,宽高比+垂直可视角度与lrbtfn等价,可以互相转换:
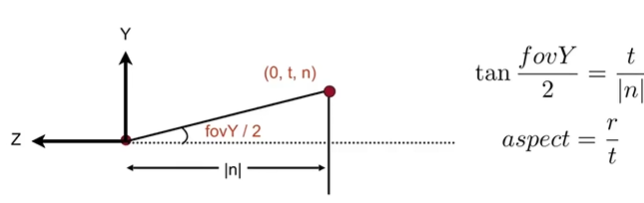
来源
[1]Games101
本文来自博客园,作者:ETHERovo,转载请注明原文链接:https://www.cnblogs.com/etherovo/p/17316010.html


 浙公网安备 33010602011771号
浙公网安备 33010602011771号