03 Transformation

关键点

• Affine Transformation (Linear Transformation, Transmation)
• Homogeneous coordinates
• Composite Transform
• 2D and 3D

1. Linear Transformation (2D for instacnce)

1.1 Scale

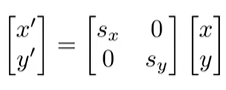
Reflection

1.2 Shear

1.3 Rotate

默认以原点为中心逆时针。

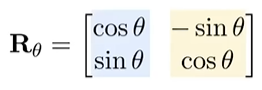
1.4 总结：Linear Transformation

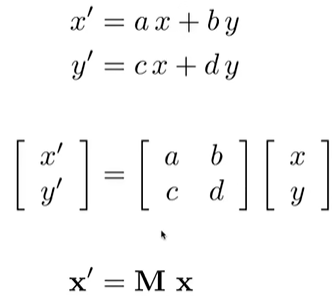
2. Homogeneous coordinates 齐次坐标 (2D for instacnce)

2.1 Translation

可见Translation不是线性变换，由此引入齐次坐标来获得统一的transformation表示方法。但是，齐次坐标带来了新问题。

2.2 Homogeneous coordinates

增加一个维度，来表示点或者向量，点的新维度值为1，而向量为0：

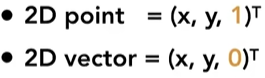
那么，点的平移变换也可以写作线性变换形式;同时，保证了向量的平移不变性：

进一步的，可以保证空间中的点或向量运算的法则：

其中，对于新坐标w不为0或1，需要变换成1获得点的标准形式。因此，对于点的加法，或者说w=2，可以看作2个点的中点。

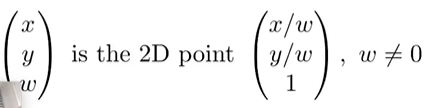
2.3 Affine Transformation 仿射变换

2.3.1 使用齐次坐标来表示仿射变换：

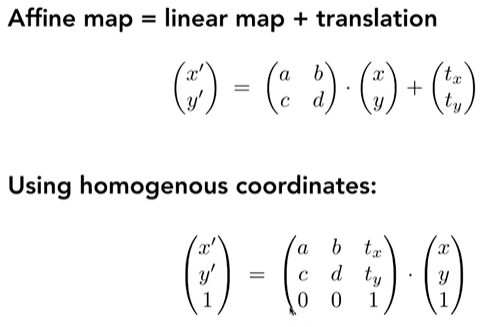
在二位情况下的规律为，左上角2x2矩阵为线性变换矩阵，右上角2x1矩阵为平移，最下面一行是[0,0,1]：

2.3.2 代价

• 点或者向量表示多了一个维度，且变换矩阵增加三个值，但是对于二维仿射变换，最下面一行是确定的，所以不需要保存。

3. Inverse Transform (2D for instacnce)

3.1 Rotate的线性变换矩阵：

• 旋转矩阵的逆矩阵被定义为：反向旋转相同大小的角度，或者说旋转相反角度。
  
• 从旋转矩阵的定义式中有，旋转相反角度的变换矩阵，是原矩阵的转置，则旋转矩阵的逆矩阵是转置矩阵。
  

4. Composite Transform (2D for instacnce)

4.1 Composite Transform

• 复杂变换可以由一系列简单变换得到。
• 矩阵乘法不满足交换律（对顺序敏感）：对于列向量表示的点，放在变换矩阵的右侧，相应的先进行的变换对应的变换矩阵在右侧。
  
• 矩阵乘法满足结合律：所有复杂变换都可以用一个3x3变换矩阵表示。
• 任意一个变换矩阵可以视作两部分操作：先进行复杂或者简单的线性变换，最后进行平移。这个可以从仿射变换的定义的到。

4.2 Decomposing Complex Transform

• 可以实现绕任意轴或点的旋转变换：
  

5. 3D Transforms

5.1 2D to 3D

5.1.1 Homogeneous Coordinates

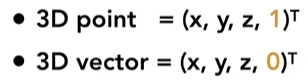
5.1.2 Transformations

对于3D仿射变换，与2D情况一致：最后一行为[0,0,0,1]，左上角为线性变换，右上角为平移。

Scale

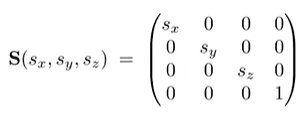
Translation

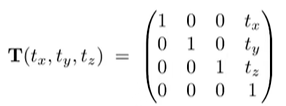
Rotate

绕坐标轴旋转：
可见，规律为：被旋转轴的对角线位置保持为1且其在线性变换矩阵中的对应行列值为零，其他位置填充二维旋转矩阵；特殊之处在于，绕y轴旋转的填充内容是二位旋转矩阵的转置，这是因为严格遵守右手坐标系（x->y->z->x）的情况下来定义旋转角度的正方向。

绕任意轴旋转：

• Euler angles （欧拉角）
  即绕x、y、z轴的旋转角度。绕任意轴旋转可以分解为绕坐标轴旋转。
• Rodriguea' Rotation Formula
  类比2D，绕任意轴旋转可以平移到原点，再旋转，最后平移得到。
  
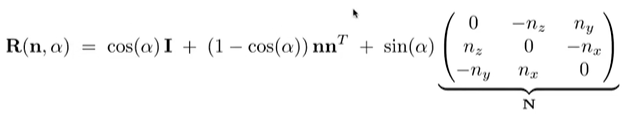
• 四元数
  旋转矩阵不适合作差值。

来源

[1]Games101