7-3 树的同构（25 分） JAVA

给定两棵树T1和T2。如果T1可以通过若干次左右孩子互换就变成T2，则我们称两棵树是“同构”的。

例如图1给出的两棵树就是同构的，因为我们把其中一棵树的结点A、B、G的左右孩子互换后，就得到另外一棵树。

而图2就不是同构的。

 

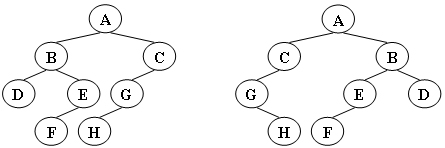
　　　　　　　　　　　　图1

 

 

 

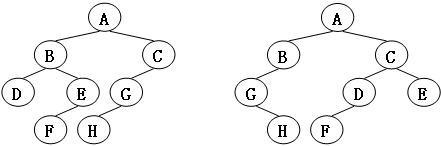
　　　　　　　　　　　　图2

现给定两棵树，请你判断它们是否是同构的。

 

输入格式:

输入给出2棵二叉树树的信息。对于每棵树，首先在一行中给出一个非负整数N (≤10)，即该树的结点数（此时假设

结点从0到 N -1 编号）；随后N行，第i行对应编号第i个结点，给出该结点中存储的1个英文大写字母、其左孩子结点的

编号、右孩子结点的编号。如果孩子结点为空，则在相应位置上给出“-”。给出的数据间用一个空格分隔。

注意：题目保证每个结点中存储的字母是不同的。

 

输出格式:

如果两棵树是同构的，输出“Yes”，否则输出“No”。

输入样例1（对应图1）：

8
A 1 2
B 3 4
C 5 -
D - -
E 6 -
G 7 -
F - -
H - -
8
G - 4
B 7 6
F - -
A 5 1
H - -
C 0 -
D - -
E 2 -

输出样例1:

Yes

输入样例2（对应图2）：

8
B 5 7
F - -
A 0 3
C 6 -
H - -
D - -
G 4 -
E 1 -
8
D 6 -
B 5 -
E - -
H - -
C 0 2
G - 3
F - -
A 1 4

输出样例2:

No

思路：

1.使用数组来表示二叉树，数组元素是二叉树的每个节点Node。节点类由三个属性：节点值element，左孩子位置left，右孩子位置right

2.需要设计两个函数：1.建二叉树；2.同构判别

3.使用StreamTokenizer类获取屏幕输入，处理输入比Scanner类效率高

建树函数：

建立二叉树的同时，我们要找出根节点的位置。

从样例可知，除了根节点，其他每个节点的编号都会出现在左右孩子编号中。标记出现的编号，未被标记的则为根节点

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.StreamTokenizer;


/**
 * @author Ethan
 * @date 2020/6/8
 * 树的重构
 */
public class Main {
　　//记录根节点位置
    static int root = -1;

    public static void main(String[] args) throws Exception {
        StreamTokenizer in = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));

        Node1[] nodes1 = buildTree(in);
        int root1 = root;
        Node1[] nodes2 = buildTree(in);
        int root2 = root;

        if (isTg(root1, nodes1, root2, nodes2)) {
            System.out.println("Yes");
        } else {
            System.out.println("No");
        }
    }

    //判断同构方法
    static boolean isTg(int root1, Node1[] a, int root2, Node1[] b) {
　　　　 //两个树均为空
        if (root1 == -1 && root2 == -1) {
            return true;

        //树a为空或树a为空
        } else if ((root1 == -1 && root2 != -1) || (root1 != -1 && root2 == -1)) {
            return false;

        //两个数的根节点是否相同
        } else if (!a[root1].element.equals(b[root2].element)) {
            return false;

        //分别判断两个树的左儿子和右儿子是否相同
        //如果相同，则将孩子节点作为根节点进行递归，一直到叶节点为止
        } else if (isTg(a[root1].left, a, b[root2].left, b) &&
                isTg(a[root1].right, a, b[root2].right, b)) {
            return true;

        //判断树a左儿子和树b右儿子是否相同   树a右儿子和树b左儿子是否相同
        //如果相同，则将孩子节点作为根节点进行递归，一直到叶节点为止
        } else {
            return isTg(a[root1].left, a, b[root2].right, b) &&
                    isTg(a[root1].right, a, b[root2].left, b);
        }

    }

    //建树方法
    static Node1[] buildTree(StreamTokenizer in) throws Exception {

        in.nextToken();
        int n = (int) in.nval;
        Node1[] tree = new Node1[n];

        int[] check = new int[n];
        for (int i = 0; i < n; i++) {
            //设置标记，先将每个节点标记为 -1
            //当节点编号出现在孩子节点编号时，将标记设为1
            check[i]=-1;
        }
        for (int i = 0; i < n; i++) {
            tree[i] = new Node1();
            in.nextToken();
            //读取元素值
            tree[i].element = in.sval;

            in.nextToken();
            //读取左孩子编号
            //ttype = -2时，说明为数字
            if (in.ttype == -2) {
                tree[i].left = (int) in.nval;
                //当节点编号出现在孩子节点编号时，将标记设为1
                check[tree[i].left] = 1;
            } else {
                //当孩子节点编号为空时，标记为 -1
                tree[i].left = -1;
            }

            in.nextToken();
            //读取右孩子编号
            if (in.ttype == -2) {
                tree[i].right = (int) in.nval;
                check[tree[i].right] = tree[i].right;
            } else {
                tree[i].right = -1;
            }
        }

        //找出根节点：未在孩子编号中出现的节点编号为根节点
        for (int i = 0; i < n; i++) {
            if (check[i] == -1) {
                root = i;
                break;
            }
        }

        return tree;
    }


}
//节点类
class Node1 {
    String element;
    int left;
    int right;
}