2019-2020 XX Open Cup, Grand Prix of Korea
2019-2020 XX Open Cup, Grand Prix of Korea
比赛收获
本场贡献:et3_tsy :G提供了思路,过了H,H爆了int,贡献WA一发,J有想法,调了1hr后,发现在特例情况复杂度退化,假了
1427314831a:过了A
Ryker0923 :过了G,提供了A的思路
一共三道题
总结:本场暴露两个问题:
1)后期乏力
前两个小时过了三题,接下来,FIJ都可以做,但是都没有比较好的想法,说明题量不够,还需要时间沉淀。
2)特例导致复杂度退化
算法在实现之前,一定要和队友多交流,多尝试几种特例,一方面看算法错没错,一方面还要看复杂度会不会退化。像et3_tsy 的J题,在处理的时候,看似是树dp,但是随着层数的增多,常数会膨胀,退化成N方,假了。
部分题解
A. 模拟
简单模拟即可,注意很多细节上的问题,以及不要重复计数
#include<bits/stdc++.h>
using namespace std;
int a[1000][1000],b[1000][1000],n,m;
int cmp(int x,int y)
{
if(x==6&&y==6)return 1;
if(x==6&&y==9)return 1;
if(x==7&&y==7)return 1;
if(x==8&&y==8)return 1;
if(x==9&&y==9)return 1;
if(x==9&&y==6)return 1;
return 0;
}
int main()
{
cin>>n>>m;
char c=getchar();
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
a[i][j]=getchar()-'0';
}
getchar();
}
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
b[n-i+1][m-j+1]=a[i][j];
}
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
if(b[i][j]==6)b[i][j]=9;
else if(b[i][j]==9)b[i][j]=6;
}
int bj=0;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
if(!cmp(a[i][j],b[i][j]))
{
bj=1;break;
}
}
if(!bj)
{
if(n%2==1&&m%2==1&&a[n/2+1][m/2+1]!=8)
bj=1;
}
if(bj){
cout<<-1;return 0;
}
int ans=0;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
if(a[i][j]!=b[i][j])ans++;
else if(a[i][j]==7)ans++;
}
cout<<ans/2;
return 0;
}
G. 图论
注意这道题是让我们从可行解里面选取最小字典序的路径,那么换言之,我们就要优先dfs去查询哪个点是能到达目标点的。
值得注意的是,因为在求向图可达性中,可能形成强连通,所以直接进行两次连续的dfs,防止漏掉点没有被标记的可达点
最后是进行对可行点形成的单向路径上进行贪心模拟的过程。至于什么时候输出too long?只要访问了已经访问过的点,就说明它在已有的一个强连通分量里面出不来了,故输出too long即可。
#include<bits/stdc++.h>
using namespace std;
int n,m,s,t,cnt,tot;
int l[200010],rd[2000010];
struct node{
int x,y,z;
}ed[600010];
bool cmp(node a,node b)
{
return a.z>b.z;
}
struct tedge{
int v,next,w;
bool u;
}e[1000010];
bool b[200010],used[200010];
void add(int x,int y,int z)
{
e[++cnt].w=y;
e[cnt].v=z;
e[cnt].next=l[x];
l[x]=cnt;
}
bool dfs(int x)
{
if(used[x])
return b[x];
used[x]=1;
for(int i=l[x];i;i=e[i].next)
{
// cout<<x<<" "<<e[i].w<<endl;
if(b[x]==1)
dfs(e[i].w);
else
b[x]=dfs(e[i].w);
}
return b[x];
}
void print()
{
for(int i=1;i<=tot;i++)
printf("%d ",rd[i]);
}
void dfs2(int x)
{
used[x]=1;
for(int i=l[x];i;i=e[i].next)
if(b[e[i].w])
{
rd[++tot]=e[i].v;
if(tot>1000000)
{
printf("TOO LONG");
exit(0);
}
if(e[i].w==t)
{
print();
exit(0);
}
else if(used[e[i].w])
{
printf("TOO LONG");
exit(0);
}
else
dfs2(e[i].w);
}
}
int main()
{
cin>>n>>m>>s>>t;
int x,y,z;
b[t]=1;
for(int i=1;i<=m;i++)
{
scanf("%d%d%d",&ed[i].x,&ed[i].y,&ed[i].z);
}
sort(ed+1,ed+m+1,cmp);
for(int i=1;i<=m;i++)
{
// cout<<ed[i].x<<" "<<ed[i].y<<" "<<ed[i].z<<endl;
add(ed[i].x,ed[i].y,ed[i].z);
}
dfs(s);
for(int i=1;i<=n;i++)used[i]=0;
// for(int i=1;i<=n;i++)cout<<b[i]<<endl;
dfs(s);
if(!b[s])
{
printf("IMPOSSIBLE");
return 0;
}
// for(int i=1;i<=n;i++)cout<<b[i]<<endl;
for(int i=1;i<=n;i++)used[i]=0;
dfs2(s);
}
/*
3 3 1 3
1 2 1
2 1 2
1 3 3
*/
H. 思维
给定两个全排列,全排列A可动,B不能动,求最小交换次数,使得Ai-Bi的绝对值之和最大。
应该先从偶数上思考,即什么时候最优,即把 1到 N/2 分为第一组,把 N/2+1 到 N分为第二组
那么我们只要保证对于任意一对Ai和Bi恰好一个属于第一组,一个属于第二组即可,显然这样最优。
而奇数大同小异,唯有不同的是最中间的那个数,它不能分到第一组和第二组中去。
接下来就是双指针贪心扫描了,分别第二组元素为第一组、第二组的情况,取min即可,注意会爆int
#include<bits/stdc++.h>
using namespace std;
#define maxn 300000
#define ll long long
#define INF 0x3f3f3f3f3f3f3f3fLL
int a[maxn],b[maxn];
ll minn(ll x,ll y)
{
return x<y?x:y;
}
int n;
double mid;
bool l(int val)
{
return val<mid;
}
bool r(int val)
{
return val>mid;
}
int main()
{
cin>>n;
mid=(0.0+n)/2+0.5;
for(int i=1;i<=n;i++)cin>>a[i];
for(int i=1;i<=n;i++)cin>>b[i];
ll ans=INF;
ll cur=0;
int cnt=0;
int apos=0,bpos=0;
cur=0;
while(cnt!=n/2)
{
while(!l(b[++bpos]));
while(!r(a[++apos]));
cur+=abs(apos-bpos);
cnt++;
}
ans=minn(ans,cur);
cur=0;cnt=0;apos=0,bpos=0;
while(cnt!=n/2)
{
while(!r(b[++bpos]));
while(!l(a[++apos]));
cur+=abs(apos-bpos);
cnt++;
}
ans=minn(ans,cur);
cout<<ans<<"\n";
return 0;
}
J.启发式合并
大致题意(经过转化之后的)
给定n个区段【l, r】, 以及对应的权值,注意他们不交叉
现在就是求 k (从1->n分别求) 层,至多叠k层的最大权值和为多少
思路
显然,我们可以发现他们不交叉只有两种情况,一种是完全包含,一种是完全不相交
这就有一个树的特征了,建树先排个序,左端第一维(越左越优),区段长第二维(越长越优),再线性扫一遍。
我们把树建好后,很显然可以在树上去算dp,但是会被下图的特例卡退化成\(O(n^2)\)
那么我们应该怎么想这道题嘞?
其实有个很核心的性质
如果我们在第k层进行贪心选择的时候,k+1层也一定会选上这些
这一点一定要理解好
那么我们理解了这个之后,只要利用堆,去存储单层最优的区段贡献即可(对于兄弟之间而言,他们不会产生影响,所以取出两边最优的相加,就是父亲的最优)
而这一过程可以利用启发式合并的思想进行优化处理
对于本题, et3_tsy 有一定的收获:
对于启发式合并而言,并不一定要依赖于树剖,它只是一种思想,就是把小的往大的上面去合并。在进行树dp的时候,一定优先考虑退化问题(比如这题可能会退化成如下情况)。

#include<bits/stdc++.h>
using namespace std;
#define maxn 252000
#define ll long long
int n,tot;
ll tmp[maxn];
int ma[maxn],in[maxn],fa[maxn];
priority_queue<ll>heap[maxn];
inline int read()
{
int ans=0;
char last=' ',ch=getchar();
while(ch<'0'|ch>'9')last=ch,ch=getchar();
while(ch>='0' && ch<='9')ans=ans*10+ch-'0',ch=getchar();
if(last=='-')ans=-ans;
return ans;
}
void merge_(int x)
{
int f=fa[x],fh=ma[f],gh=ma[x];
if(heap[fh].size()<heap[gh].size())
{
ma[f]=gh;
swap(fh,gh);
}
int cnt=0;
while(!heap[gh].empty())
{
tmp[cnt++]=heap[gh].top()+heap[fh].top();
heap[gh].pop(),heap[fh].pop();
}
for(int i=0;i<cnt;i++)heap[fh].push(tmp[i]);
}
struct ed
{
int l,r;
ll val;
bool operator<(const ed& sec)const
{
if(l!=sec.l)return l<sec.l;
return r>sec.r;
}
}e[maxn];
inline bool check(int l,int r,int curl,int curr)
{
return l<=curl&&r>=curr;
}
int main()
{
cin>>n;
for(int i=1;i<=n;i++)
{
e[i].l=read(),e[i].r=read(),e[i].val=read();
e[i].r--;
}
sort(e+1,e+n+1);
int curindex=0;
for(int i=1;i<=n;i++)
{
while(curindex&&!check(e[curindex].l,e[curindex].r,e[i].l,e[i].r))
{
curindex=fa[curindex];
}
fa[i]=curindex;
curindex=i;
}
queue<int>node;
for(int i=1;i<=n;i++)
{
ma[i]=i;
in[fa[i]]++;
}
for(int i=1;i<=n;i++)
if(in[i]==0)node.push(i);
while(!node.empty())
{
int x=node.front();
node.pop();
if(x==0)break;
heap[ma[x]].push(e[x].val);
merge_(x);
in[fa[x]]--;
if(in[fa[x]]==0)node.push(fa[x]);
}
ll ans=0;
for(int i=1;i<=n;i++)
{
if(!heap[ma[0]].empty())
{
ans+=heap[ma[0]].top();
heap[ma[0]].pop();
}
cout<<ans<<" ";
}
return 0;
}
F. Hilbert's Hotel 线段树
题意:有一家旅馆(有多个房间,序号从0开始)和多个旅行团,现给定三种操作:
1 k
表示新来一个旅行团有k个人.
当k>0时所有旅馆中已有的人往后移k个房间;
当k=0时表示来了数不清的人,此时所有旅馆中已有的人移到自己房间标号2倍的房间,再将新加入的人安排在房间号为奇数的房间中。
2 g x
访问第g个旅行团的第x小的人在那个房间,结果对le9+7取模(g<=当前已有的旅行团个数,1<=x<=第g个旅行团的人数)
3 x
访问当前第x个房间的人来自那个旅行团(x<=1e9)
题解:
对于第二种询问,我们可以考虑对每一个旅行团的人所在位置用一个函数\(y=kx+b\)维护
当k>0时将所有的已有的bi加上k,再新加入一组\(k=1,b=1e9+6\)
当k=0时将所有已有的ki和bi乘2,再新加入一组\(k=2,b=1e9+6\)
开两颗线段树分别去维护k和b即可。
对于第三种询问,我们考率从x这个位置向前回溯已有的操作,以确定x来自那个旅行团
如若当前k>0时,如果k>x则x一定来自当前操作所在的旅行团,否则令x-=k,回溯上一步操作
若当前k=0,如果x为奇数,则x来自当前旅行团,否则令x=x/2,回溯上一步操作
对于k>0的回溯访问,暴力维护复杂度为n,考虑维护所有连续的k>0的和,在此区间上进行二分答案,即可优化为logn
对于k=0的回溯访问,当x>0时每次至少减少一半,复杂度为logn,但若一开始时x=0,则需跳过这个连续的k=0的区间,否则会进行多次无意义的除二的操作。
#include<iostream>
#include<algorithm>
using namespace std;
const int p=1e9+7;
struct tnode{
long long l,r,num,plz,mlz;
}t[1200040][2];
long long x,y,z,bj,a[300010],binary[300010],caozuo[300100],l1[300010],l2[300010],b[300010];
inline void build(int g,int i,int l,int r)
{
t[i][g].l=l;t[i][g].r=r;
if(l==r){
// t[i][g].num=a[l]%p;
return;
}
int mid=(l+r)>>1;
build(g,i<<1,l,mid);
build(g,(i<<1)+1,mid+1,r);
t[i][g].num=(t[i<<1][g].num+t[(i<<1)+1][g].num)%p;
}
inline void pushdown(int g,int i)
{
long long k1=t[i][g].plz,k2=t[i][g].mlz;
t[i<<1][g].num=(t[i<<1][g].num*k2+k1*(t[i<<1][g].r-t[i<<1][g].l+1))%p;
t[(i<<1)+1][g].num=(t[(i<<1)+1][g].num*k2+k1*(t[(i<<1)+1][g].r-t[(i<<1)+1][g].l+1))%p;
t[i<<1][g].plz=(t[i<<1][g].plz*k2+k1)%p;
t[(i<<1)+1][g].plz=(t[(i<<1)+1][g].plz*k2+k1)%p;
t[i<<1][g].mlz=t[i<<1][g].mlz*k2%p;
t[(i<<1)+1][g].mlz=t[(i<<1)+1][g].mlz*k2%p;
t[i][g].plz=0;
t[i][g].mlz=1;
return;
}
inline void add(int g,int i,int l,int r,long long k)
{
if(t[i][g].l>r||t[i][g].r<l)return;
if(l<=t[i][g].l&&r>=t[i][g].r)
{
t[i][g].num=(t[i][g].num+k*(t[i][g].r-t[i][g].l+1))%p;
t[i][g].plz=(t[i][g].plz+k)%p;
return;
}
pushdown(g,i);
if(t[i<<1][g].r>=l)add(g,i<<1,l,r,k);
if(t[(i<<1)+1][g].l<=r)add(g,(i<<1)+1,l,r,k);
t[i][g].num=(t[i<<1][g].num+t[(i<<1)+1][g].num)%p;
return;
}
inline void mul(int g,int i,int l,int r,long long k)
{
if(t[i][g].l>r||t[i][g].r<l)return;
if(l<=t[i][g].l&&t[i][g].r<=r)
{
t[i][g].num=t[i][g].num*k%p;
t[i][g].plz=t[i][g].plz*k%p;
t[i][g].mlz=t[i][g].mlz*k%p;
return;
}
pushdown(g,i);
if(t[i<<1][g].r>=l)mul(g,i<<1,l,r,k);
if(t[(i<<1)+1][g].l<=r)mul(g,(i<<1)+1,l,r,k);
t[i][g].num=(t[i<<1][g].num+t[(i<<1)+1][g].num)%p;
return;
}
inline long long sum(int g,int i,int l,int r)
{
if(t[i][g].l>r||t[i][g].r<l)return 0;
if(t[i][g].l>=l&&t[i][g].r<=r)
{
return t[i][g].num%p;
}
pushdown(g,i);
long long res=0;
if(t[i<<1][g].r>=l)res=(res+sum(g,i<<1,l,r))%p;
if(t[(i<<1)+1][g].l<=r)res=(res+sum(g,(i<<1)+1,l,r))%p;
return res%p;
}
int main()
{
//freopen("std.in","r",stdin);
//freopen("std.out","w",stdout);
int m;
cin>>m;
build(0,1,0,m);
build(1,1,0,m);
for(int i=1;i<=4*m;i++)
{
t[i][0].mlz=1;
t[i][1].mlz=1;
}
// cout<<sum(1,2,n)<<endl;
int k,tot=0;
add(0,1,0,0,1);
add(1,1,0,0,p-1);
while(m--)
{
scanf("%d",&bj);
if(bj==1)
{
tot++;
scanf("%d",&k);
if(k)
{
a[tot]=k;
if(caozuo[tot-1]==1)l1[tot]=l1[tot-1];
else l1[tot]=tot;
caozuo[tot]=1;
add(1,1,0,tot-1,k);
add(1,1,tot,tot,p-1);
add(0,1,tot,tot,1);
}
else
{
caozuo[tot]=2;
if(caozuo[tot-1]==2)l2[tot]=l2[tot-1];
else l2[tot]=tot;
mul(0,1,0,tot-1,2);
mul(1,1,0,tot-1,2);
add(0,1,tot,tot,2);
add(1,1,tot,tot,p-1);
}
a[tot]+=a[tot-1];
}
if(bj==2)
{
int g,x;
scanf("%d%d",&g,&x);
k=sum(0,1,g,g);
int b=sum(1,1,g,g);
printf("%lld\n",(1ll*k*x+b)%p);
}
if(bj==3)
{
int x;
scanf("%d",&x);
int cnt=tot;
while(cnt>0)
{
if(caozuo[cnt]==1)
{
int l=l1[cnt],r=cnt;
if(a[r]-a[l-1]<=x)
{
x-=a[r]-a[l-1];
cnt=l-1;
}
else
{
int mid=(l+r)>>1;
while(l<r-1)
{
mid=(l+r)>>1;
if(a[cnt]-a[mid-1]>x)l=mid;
else r=mid;
}
if(x<a[cnt]-a[r-1])
{
cnt=r;break;
}
else
{
cnt=l;break;
}
}
}
else
{
if(x&1)break;
if(x==0)
{
cnt=max(l2[cnt]-1,0ll);
break;
}
else
{
x>>=1;
cnt--;
}
}
}
printf("%d\n",cnt);
}
}
return 0;
}
I.最小直径生成树
这道是一道板子题
求最小直径生成树,在oi-wiki上有相关内容
先用Floyd或者Johnson跑出全员最短路
再对每个点排序一遍去确定自远及近的点是谁
下面来确定绝对中心
绝对中心可能是边,可能是点
对于点来讲,它只要选择最远的两个点作为最远的点,其他点都比他小,相加就是他们的直径。跑一遍迪杰斯特拉即可
对于边来说,我们找到绝对中心对应的边之后,对于它两个边上的点u,v初始化不应该都是0,否则就会出现下面的错误,。假定我们的绝对中心在4这条蓝色边上,它两端初始化的dis均是0,对于箭头指向的点,选绿3,或者紫1,在dij中均是等价的,但是我们很容易发现,在直径的求解中,如果选紫1显然它的值会更小(因为它的产生的代价已经由黑3承担了)
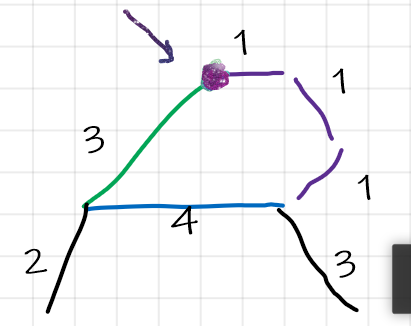
为了处理这个问题,最小直径生成树提出了一个思路
它的绝对中心一开始在中间,谁的最远距离远就离谁近
如果记绝对中心距离u点的距离为\(disu\),由u点支配的最远的点距离u的距离为\(faru\)
绝对中心距离v点的距离为\(disv\),由v点支配的最远的点距离v的距离为\(farv\)
绝对中心所属的这条边权值是\(w.val\),那么有:
$disu=(w.val+farv-faru){\div}2 $
$disv=(w.val+faru-farv){\div}2 $
上面的问题就引刃而解了,即绝对中心会更加靠近最远的点
很显然,这一类题目很容易爆int以及用精度写有点浪费,所以干脆全部乘以2,以及后面的dij压边的时候记得全部乘以2即可
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define maxn 505
#define INF 0x3f3f3f3f3f3f3f3fLL
#define int ll
inline ll read()
{
ll ans=0;
char last=' ',ch=getchar();
while(ch<'0'|ch>'9')last=ch,ch=getchar();
while(ch>='0' && ch<='9')ans=ans*10+ch-'0',ch=getchar();
if(last=='-')ans=-ans;
return ans;
}
ll min(ll a,ll b)
{
return a>b?b:a;
}
int n,m,a,b,c;
ll initu=0;
int ansu=0,ansv=0;
ll curans=INF;
struct E
{
int u,v,val;
E(int a,int b,int c){u=a;v=b;val=c;}
};
struct so
{
int val;
int id;
bool operator<(const so& sec)const
{
return val>sec.val;
}
}ss[maxn<<2];
struct dij
{
ll val;
int nxt;
int from;
bool operator<(const dij& sec)const
{
return val>sec.val;
}
dij(ll a,int b,int c){val=a;nxt=b;from=c;}
};
vector<E>e;
vector<int>node[maxn];
ll dis[maxn][maxn];
int opt[maxn][maxn];
ll vis[maxn];
bool been[maxn];
priority_queue<dij>heap;
void getans(int curnum)
{
E& cured=e[curnum];
int u=cured.u;
int v=cured.v;
for(int p=1,i=2;i<=n;i++)
{
if(dis[v][opt[u][i]]>dis[v][opt[u][p]])
{
if(curans>cured.val+dis[u][opt[u][i]]+dis[v][opt[u][p]])
{
curans=cured.val+dis[u][opt[u][i]]+dis[v][opt[u][p]];
initu=curans-dis[u][opt[u][i]]*2;
ansu=u,ansv=v;
}
p=i;
}
}
return;
}
signed main()
{
n=read(),m=read();
memset(dis,INF,sizeof(dis));
for(int i=0;i<=n;i++)dis[i][i]=0;
for(int i=0;i<m;i++)
{
a=read(),b=read(),c=read();
node[a].push_back(e.size());
e.emplace_back(a,b,c);
node[b].push_back(e.size());
e.emplace_back(b,a,c);
dis[a][b]=c;
dis[b][a]=c;
}
for(int k=1;k<=n;k++)
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
{
if(dis[i][k]+dis[k][j]<dis[i][j])dis[i][j]=dis[i][k]+dis[k][j];
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
ss[j].id=j,ss[j].val=dis[i][j];
sort(ss+1,ss+n+1);
for(int j=1;j<=n;j++)
opt[i][j]=ss[j].id;
}
for(int i=0;i<e.size();i+=2)
{
getans(i);
}
for(int i=1;i<=n;i++)
{
if(dis[i][opt[i][1]]+dis[i][opt[i][2]]<curans)
{
curans=dis[i][opt[i][1]]+dis[i][opt[i][2]];
ansu=ansv=i;
}
}
cout<<curans<<"\n";
memset(vis,INF,sizeof(vis));
vis[ansu]=initu;
heap.push(dij(vis[ansu],ansu,ansu));
if(ansu!=ansv)
{
vis[ansv]=dis[ansv][ansu]*2-initu;
heap.push(dij(vis[ansv],ansv,ansu));
}
int curcnt=0;
while(!heap.empty()&&curcnt<n)
{
dij curx=heap.top();heap.pop();
if(been[curx.nxt])continue;
been[curx.nxt]=1;
curcnt++;
if(curx.nxt!=curx.from)cout<<curx.nxt<<" "<<curx.from<<"\n";
for(int k:node[curx.nxt])
{
int nxt=e[k].v;
if(!been[nxt]&&vis[curx.nxt]+e[k].val*2<vis[nxt])
{
vis[nxt]=vis[curx.nxt]+e[k].val*2;
heap.push(dij(vis[nxt],nxt,curx.nxt));
}
}
}
return 0;
}





