洛谷P4170涂色 + HDU2476：String painter(区间DP)

洛谷P4170涂色 + HDU2476：String painter(区间DP)

两题有相似之处，HDU的是洛谷P4170的变形题

洛谷P4170

https://www.luogu.com.cn/problem/P4170

HDU2476

http://acm.hdu.edu.cn/showproblem.php?pid=2476

---

洛谷P4170

题意

给定一个目标字符串，每次操作可以选定某个连续区段将其均改成同一个字符（一开始均为空），问要至少要进行几次才能染成目标字符串，字符串长度小于50

思路

采用区间DP，那么我们如何建立状态转移关系呢？

在确定具体的关系之前，我们应该先思考一下进行贪心的方案

比如说，我们现在要染

ABAA

它需要几步嘞？显然两步，即

0000 -> AAAA -> ABAA

我们在处理连续且相同的前后缀时，优先染他们

这种方案不会影响我们接下来对中间区段的染色，

并且它能为我们节省不必要的一步！！！

有了这个贪心思想，我们可以观察一下我们某个区段的情况了，

如下图，我们假设现在研究：[j,i]这个区段的情况

那么为了应用上面的贪心方案，我们实际上是要研究[j+1,i] 与 最左端 j 的关系

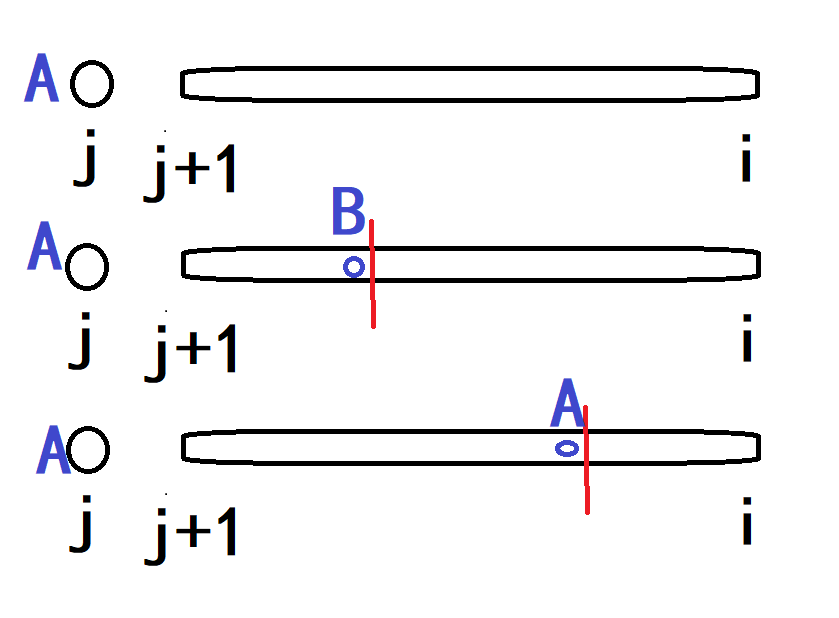
假设红色线表示分割线，那么它表示说左边部分和右边部分的染色策略相互独立

上面提供了三种分割的方案

1）这个区段啥也不切

2）这个区段切的无意义

3）这个区段切完后，左半边的最右端恰好与 j 相同

第二种分割方式显然劣于第一种

在第三种情况中，我们就很好的将上面的贪心方案应用了起来，

所以我们列状态转移只要考虑第一、三种情况即可

最优染色的状态转移关系如下

$$dp\left[l\right]\left[r\right]=min\{1+dp[l+1]\left[r\right],min\{dp\left[l\right]\left[k\right]+dp[k+1]\left[r\right]\mid s\left[l\right]=s\left[k\right]\}\}$$

最后要小心一下区段左右端l,r遍历的顺序即可

AC代码：

#include<iostream>
#include<cstring>
#include<cstdio>
#include<string>
using namespace std;
#define INF 0x3f3f3f3f
#define maxn 105
#define minn -105
#define ll long long int
#define ull unsigned long long int
#define uint unsigned int
inline int read()
{
    int ans=0;
    char last=' ',ch=getchar();
    while(ch<'0'|ch>'9')last=ch,ch=getchar();
    while(ch>='0'&&ch<='9')ans=ans*10+ch-'0',ch=getchar();
    if(last=='-')ans=-ans;
    return ans;
}
string s2;
int dp[maxn][maxn],ans[maxn];
void solve()
{
    memset(dp,0,sizeof(dp));
    memset(ans,0,sizeof(ans));
    int len=s2.size();
    for(int i=0;i<len;i++)
    {
        for(int j=i;j>=0;j--)
        {
            dp[j][i]=dp[j+1][i]+1;
            for(int k=j+1;k<=i;k++)
            {
                if(s2[j]==s2[k])
                    dp[j][i]=min(dp[j][i],dp[j+1][k]+dp[k+1][i]);
            }
        }
    }
    cout<<dp[0][len-1]<<endl;
}


int main()
{
    cin>>s2;
    solve();
    return 0;
}

HDU2476

题意

给你两个字符串，每次操作你可以选定某个连续区段将其均改成同一个字符，问至少多少次能够让s1到s2，字符串长度小于100

思路

这是一道区域赛的题

这道题与上一道大相径庭

唯一区别就是它初始是有原字符串的

那么与上面一题处理起来基本一样，要优先看看如何染色是最优的

处理完上面的东西后，我们现在就知道了某个区段染色的最佳方案

接下来我们要看的是，如何利用原有的字符串将来减少染色次数

我们想如果某个区段最右端颜色已经一样了，那么我们就没有染色的意义了

基于此思想，我们就可以开一个数组ans[i],记录 [0,i] 这个区段的最优值

如果i+1颜色不用变了，有ans[i+1] = ans[i]

否则，i+1的颜色肯定要改变，那么它肯定要归属于某种最优区段的划分方案中，

即通过枚举划分点，从前继状态 ans[k] + dp[k][i+1] 找最优即可

AC代码：

#include<iostream>
#include<cstring>
#include<cstdio>
#include<string>
using namespace std;
#define INF 0x3f3f3f3f
#define maxn 105
#define minn -105
#define ll long long int
#define ull unsigned long long int
#define uint unsigned int
inline int read()
{
    int ans=0;
    char last=' ',ch=getchar();
    while(ch<'0'|ch>'9')last=ch,ch=getchar();
    while(ch>='0'&&ch<='9')ans=ans*10+ch-'0',ch=getchar();
    if(last=='-')ans=-ans;
    return ans;
}
string s1,s2;
int dp[maxn][maxn],ans[maxn];
void solve()
{
	memset(dp,0,sizeof(dp));
    memset(ans,0,sizeof(ans));
    int len=s1.size();
    for(int i=0;i<len;i++)
    {
        for(int j=i;j>=0;j--)
        {
            dp[j][i]=dp[j+1][i]+1;
            for(int k=j+1;k<=i;k++)
            {
            if(s2[j]==s2[k])
                dp[j][i]=min(dp[j][i],dp[j+1][k]+dp[k+1][i]);
            }
        }
    }
    for(int i=0;i<len;i++)
        ans[i]=dp[0][i];
    for(int i=0;i<len;i++)
    {
        if(s1[i]==s2[i])
        ans[i]=ans[i-1];
        else
        {
            for(int j=0;j<i;j++)
            {
                ans[i]=min(ans[i],ans[j]+dp[j+1][i]);
            }
        }

    }
    cout<<ans[len-1]<<endl;
}


int main()
{
    while(cin>>s1>>s2)solve();
    return 0;
}