割点

割点

含义之类的自行百度

标程

洛谷P3388

#include<iostream>
#include<cstring>
#include<cstdio>
#include<stack>
#include<algorithm>
#include<vector>
using namespace std;
#define INF 0x3f3f3f3f
#define maxn 100005
#define minn -105
#define ll long long int
#define ull unsigned long long int
#define uint unsigned int
int n,m;
int fvis[maxn],low[maxn];
bool ans[maxn];
int index_(0);
int cur_fa;
vector<int>node[maxn];

void dfs(int cur)
{
    int num=0;
    index_++;
    low[cur]=fvis[cur]=index_;
    for(int i=0;i<node[cur].size();i++)
    {
        int nxt=node[cur][i];
        if(!low[nxt])
        {
            dfs(nxt);
            low[cur]=min(low[cur],low[nxt]);
            if(low[nxt]>=fvis[cur]&&cur!=cur_fa)ans[cur]=1;
            if(cur==cur_fa)num++;
        }
        else low[cur]=min(low[cur],fvis[nxt]); //本处是下面要讨论的地方
    }
    if(cur==cur_fa&&num>1)ans[cur]=1;
}

int main()
{
    cin>>n>>m;
    memset(low,0,sizeof(low));
    memset(ans,0,sizeof(ans));
    memset(fvis,0,sizeof(fvis));
    for(int i=0;i<m;i++)
    {
        int a,b;
        cin>>a>>b;
        node[a].push_back(b);
        node[b].push_back(a);
    }
    for(int i=1;i<=n;i++)
        if(!low[i])cur_fa=i,dfs(i);
    int sum=0;
    for(int i=1;i<=n;i++)
        if(ans[i])sum++;
    cout<<sum<<endl;
    for(int i=1;i<=n;i++)
        if(ans[i])cout<<i<<" ";
    cout<<endl;
    return 0;
}

讨论点

else low[cur]=min(low[cur],fvis[nxt]);

由于点与点联通的无向关系，那么在进行dfs的时候，我们尝试去遍历的nxt只能有两类情况

1）它未被dfs

2）它已经在dfs形成的栈中

第一种情况更新一定是更新成当前孩子的low，这与求scc（强连通分量）的思路类似

那么第二种情况中，为什么是更新成fvis（首次访问的时间），而不是low呢？

即：

else low[cur]=min(low[cur],low[nxt]);

请看下图

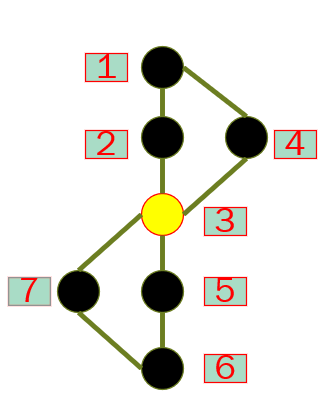
标号为遍历顺序

而现在让我们看看本来是割点的3号点是如何被忽视的吧

首先我们访问完了1234,

4,3无论按照上面何种方案，均会被改成1

我们继续遍历到7，这个时候问题就来了

到底标号7是取fvis[3]还是low[3]呢?

如果取low[3]，又low[3]在前一过程中已经被更新成为了1

那么low[7]也就成了1

low[6],low[5]也跟着变成了1

这样一来割点3就被我们忽视了

那么核心毛病出在哪嘞？

在求强连通分量的过程中，我们上面两种写法都可以，对于scc而言，上面这种连圈型是一个强连通分量，从遍历角度上看，本质是一个圈，只不过中间有点交叉罢了

而对于研究割点问题而言，它研究的是极小圈，也就是说看的是最直接的那两个圈，我们找割点就是将他们能分离的点

两者有莫大的区别