强连通分量SCC 2-SAT
强连通分量SCC 2-SAT
部分资料来自:
1.https://blog.csdn.net/whereisherofrom/article/details/79417926
2.https://baike.baidu.com/item/%E5%BC%BA%E8%BF%9E%E9%80%9A%E5%88%86%E9%87%8F/7448759?fr=aladdin
定义
在有向图G中,如果两个顶点vi,vj间(vi>vj)有一条从vi到vj的有向路径,同时还有一条从vj到vi的有向路径,则称两个顶点强连通。如果有向图G的每两个顶点都强连通,称G是一个强连通图。有向图的极大强连通子图,称为强连通分量。强连通分量中,对于任意两个元素,相互存在有向路径。
注意:单独一个点也是强连通分量。

像这里,{1,2,3,4},{5}就是强连通分量
一般而言,强连通分量之间也会存在一定关系。所以首先,我们要建立对每个强连通分量中的元素i建立一个映射scc[i],通过映射的不同来区分两个点是否属于同一个强连通分量。
而强连通分量之间关系的建立,是通过枚举所有边。比如我现在枚举到了E(u,v),
如果映射scc[u]和scc[v]不相同,那么就可以依据u与v本身的关系,对u和v所在的强连通分量进行对应关系的建立。
这一过程也叫缩图。
当然,建立强连通分量关系的时候可能会有重边,那么要看实际问题当中是否会产生影响。
那么我们如何求强连通分量嘞?
主要有三个主流算法,算法复杂度都是O(V+E)级别的,分别为Kosaraju、Tarjan、Gabow
1.Kosaraju 算法
它建立的基础是强连通定义的推论:原图的强连通分量和反图的强连通分量一致
大致思路:
1.前向星建边,建两张图:原图G和反图G':

2.对反图G'求一次后序遍历,按照遍历完毕的先后顺序将所有顶点记录在数组order中。
3.按照order数组的逆序,对原图G求一次先序遍历,标记连通分量。
具体过程:
1.反图的后序遍历
利用vector建原图,反图。
对反图进行后序dfs,按照访问完成的顺序,将节点添加到数组order,这个order表示的是时间戳,以表示时间的先后
如下图,order[N]={9,8,7,2,3,4,1,5,11,10,6}
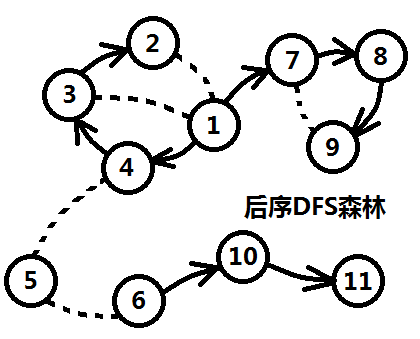
2.原图的先序遍历
第二步,按照order的反向顺序,对原图求一次先序dfs。标记连通块。
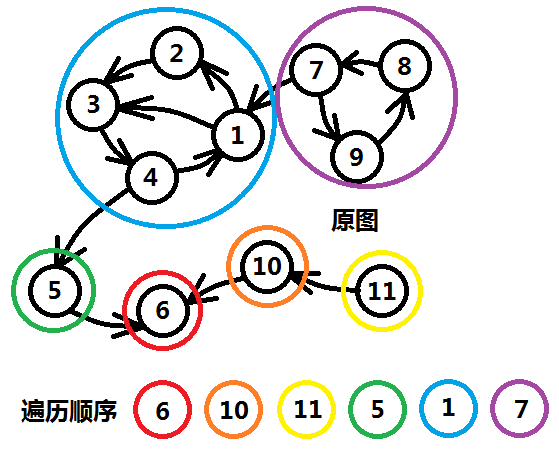

两次DFS的时间复杂度均为O(V+E)
原理说明
对于强连通内各个顶点:
从强连通分量的定义出发,如果两个顶点a和b,a能够到b,b也能够到a,则a和b属于同一个强连通。
对反图上的两个点a和b,如果a能够到b,则a的时间戳必定大于b,也就是说原图中b一定能到a。
那么如果在原图中,a也能够到b,那么由定义可知a和b属于同一个强连通。
对于强连通分量之间
Kosaraju算法的高明之处就在于处理强连通分量的关系上面。
两个强连通分量之间可能存在先后关系,比如A->B,那么为了防止建立强连通分量A的时候把B也并入,思路应该是先建立B,后建立A。Kosaraju算法的精髓就在于使用反图,将两者关系转换成B->A,那么根据出栈关系,A先被保存,B后被保存,那么A的建立一定在B之后,这样就不会产生上述的问题。
(如图A是紫圈所包含的强连通分量,B是蓝圈所包含的强连通分量)
2.Tarjan算法
利用了栈的性质,可以在O(V+E)的线性时间内求出有向图的强连通分量。
并且它只需要一次深度优先遍历。
所以无论在算法时间复杂度,还是编码复杂度上,都优于Kosaraju算法。
算法描述
存储内容
栈 st[top] 存储正在进行遍历的结点
时间戳数组 fvis[u] 结点u第一次被遍历到的时间戳
追溯数组 src[u] 在遍历时,结点u能够追溯到的祖先结点中时间戳最小的值
算法过程
(a)对所有未被标记的结点u调用Tarjan(u)
(b)Tarjan(u)是一个深度优先搜索
(1)标记fvis[u]和src[u]为当前时间戳,将u入栈;
(2)访问和u邻接的所有结点v;
如果v未被访问,则递归调用Tarjan(v),调用完毕更新src[u]=min{src[u],src[v]};
如果v在栈中,则更新src[u]=min{src[u],fvis[v]};(后者其实也可以也成是stc[v],没问题的)
(3)u邻接结点均访问完毕,如果src[u]和fvis[u]相等,则当前栈中此元素及叠在此元素以上的所有元素属于同一个强连通分量,出栈,标记scc数组;
详细图示过程请看:https://blog.csdn.net/WhereIsHeroFrom/article/details/79417926
后面洛谷板子P3387也写的比较清楚。
2-SAT
SAT是Satisfiability的缩写,可满足性,而2表示0,1两种布尔量
模型
给定一串布尔变量,每个变量只能为真或假。要求对这些变量进行赋值,满足布尔方程(包括异或,或,与)
【例】给定一些逻辑关系式X op Y = Z。其中op的取值为(AND,OR,XOR),
X,Y,Z的取值为[0,1],其中X和Y为未知数,给定未知数和关系式的个数(N,M<100000),
求是否存在这样一种解满足所有关系式,存在输出YES,否则NO。
如我们给定:
X1 AND X2 == 0
X2 OR X3 == 1
X3 XOR X1 == 1
给出上面三个式子,求X1,X2,X3(x只能取0,1)
显然X1=0 X2=1 X3=1
一旦关系很多,未知量很多,问题就变得很棘手了。
解法
朴素算法是枚举,因为每个数的取值只有两种,所以可以枚举每个数是0还是1,然后判断它所在的所有等式中是否满足条件。
这个枚举的开销是非常大的,因为每个数都有两种情况,所以总的时间复杂度势必为O(2^N)。
对于这类问题,我们可以利用数形结合,将这个数字问题转化成图论问题
对于N个变元,我们对每个变元x,各建立x=1,x=0这两个命题,命题一一映射成点,我们就有2N个孤立的点,
存储上,对于Xi而言,点i表示命题Xi=0,点i+n表示命题Xi=1
通过枚举条件关系式,来建立有向边,这里的有向,实质表示离散数学中的“蕴含”
换言之,我们正是要将蕴含关系转换成有向关系,如下面所示:
X AND Y,对于这样一个逻辑表达式,我们可以得出这样一个事实:
a) X AND Y==0,可以得出:如果X为1,则Y必定为0;同理,如果Y为1,则X必定为0;
b) X AND Y==1,可以得出:X和Y都为1;我们还可以这样说:如果X为0,则X必为1;同理,如果Y为0,则Y必为1;(这里要注意!)
那么我们可以像下面这样建立命题之间的关系:
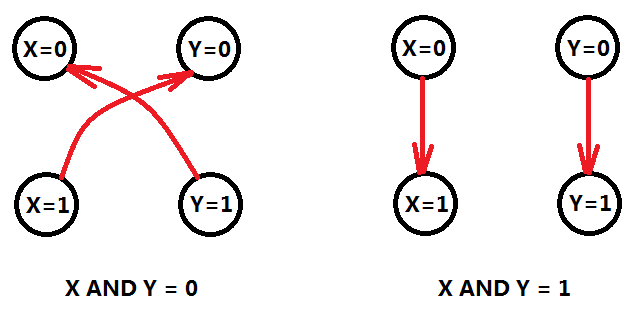
如果X=1则Y=0,建立有向边(X=1)=>(Y=0),同理(Y=1)=>(X=0)。那么X AND Y = 1的情况,也采用类似的方法建立有向边。(注意左边不能反着写)
同样,我们发现OR和XOR也可以采用类似的方法,建立有向边。
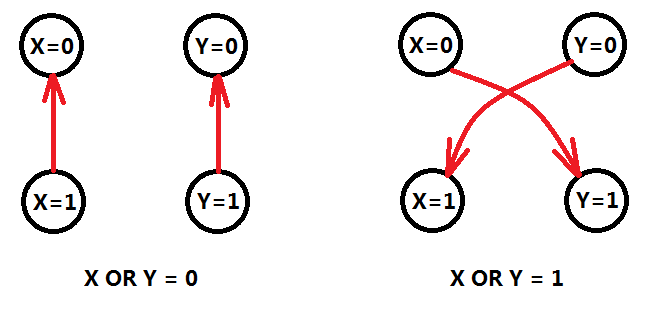
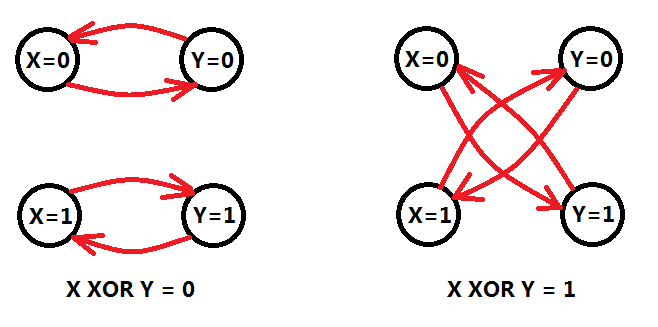
当我们建立了有向边,求一次强连通分量。然后一次线性扫描,判断某个点X的两种取值(X=0)和(X=1)如果在同一个强连通分量,则等式组无解,否则必定存在至少一组解。Why?
一旦出现强连通,因为Xi=0 => Xi=1,Xi=1 => Xi=0,则Xi=0 <=> Xi=1, 显然矛盾,故无解
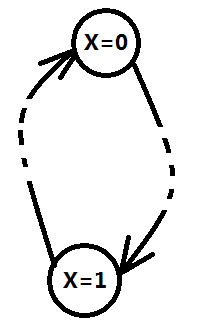
由于有向表示的是蕴含关系,根据离散数学芝士可知,若a => b成立,它的逆反关系!b => !a,也必然成立,那么,我们可以得到一个推论:任意一个强连通分量,若它的元素数大于1,则必定存在一个与之对于的逆反强连通分量(名词是我瞎编的,能会意即可)
因为上述两个分量都成立,所以,当元素数大于1时,强连通分量与他的逆反强连通分量中,一个包含的所有命题全为真,一个包含的所有命题全为假
那么现在对于一组布尔方程,可能会有多组解同时成立。那么我们如何求解其中一组解?
应从考虑scc[i]和scc[n+i]的关系上入手
因为他们不属于同一个强连通分量,所以一定存在scc[i]<scc[n+i]或scc[i]>scc[n+i]
也就说我们对任意元素i有两种可行赋值方式(赋的是下面关系的真值):
第一种方式,scc[i]<scc[n+i]
第二种方式,scc[i]>scc[n+i]
那么究竟哪种方式真正可行,接下来我们分情况分析一下
(1)对于任意一个元素数大于1的强连通分量及其它的逆反强连通分量而言
显然两种方式都是可行的
(2)对于只有一个元素的强连通分量而言
它的形成一般是关系退化形成的,例如:x1为0或x1为0,本来!x1=>x1的两条有向边就退化成了一条有向边
求强连通分量的时候,我们是以dfs顺序,所以肯定是先建后件再建前件,也就是说后件对应的scc一定小于前件的scc,下面我们来分类讨论一下.(下面的早指的是scc值小)
第一种方式处理中:
若为真,x=1,x=0比x=1早,若存在x=1 => x=0 (若前件为假,永真,下同),关系成立
若为假,x=0,x=1比x=0早,若存在x=0 => x=1, 关系成立
第二种方式处理中:
若为真,x=1,x=1比x=0早,若存在x=1 => x=0,矛盾!
若为假,x=0,x=0比x=1早,若存在x=0 => x=1,矛盾!
只有第一种方式适用
综上,我们对所有变元Xi赋值命题scc[i]<scc[n+i]的真值,即为解
(值得一提的是,如果你从一开始x=1,x=0两个命题的存储方式对调,那么这里应该选择方式二,为了不必要的错误,上面推一种情况得出结论较为稳妥)
具体板子看下面P4782 【模板】2-SAT 问题
洛谷板子P3387 缩点+拓扑+dp
#include<iostream>
#include<cstring>
#include<vector>
#include<queue>
using namespace std;
#define INF 1e10+5
#define maxn 100005
#define MINN -105
typedef long long int ll;
int n,m;
int src[maxn],v[maxn],fvis[maxn],scc[maxn],st[maxn];
int cnt,scc_index,curtime;
vector<int>save[maxn];
//检查当前栈中是否有查找元素,当然更好的话就开个数组来存
bool check(int _checknum)
{
for(int i=1;i<=cnt;i++)
if(st[i]==_checknum)return 1;
return 0;
}
//dfs 遍历图
void dfs(int pos)
{
curtime++;//时间
src[pos]=fvis[pos]=curtime;//记录时间戳
st[++cnt]=pos;//push into stack
vector<int>::iterator it=save[pos].begin();
//be careful, this 'it' cannot be used as a static one
for(;it!=save[pos].end();it++)
{
if(check(*it)){src[pos]=min(src[pos],fvis[*it]);continue;}
//如果当前欲访问的子点处于回溯栈中,更新src
if(!src[*it])dfs(*it),src[pos]=min(src[pos],src[*it]);
//only after dfs does fathernode need to be renew
/*这个地方很重要,就是当SCC A能->SCC B时,在SCC B已经被构建了后,A不能再重复访问SCC B中含的点*/
}
//当子节点搜索结束,进行判断,如果1,标记强连通
if(src[pos]==fvis[pos])
{
while(st[cnt]!=pos)
scc[st[cnt]]=scc_index,cnt--;//pop
scc[st[cnt]]=scc_index,cnt--;scc_index++;//pop top
}
return;
}
int main()
{
cin>>n>>m;
int a,b;
for(int i=1;i<=n;i++)cin>>v[i],src[i],scc[i]=0;
for(int i=1;i<=m;i++)
{
cin>>a>>b;
save[a].push_back(b);//use nodelist to save edges
}
scc_index=1,curtime=0;
for(int i=1;i<=n;i++)
{
cnt=0;//stack is set to be empty for dfs
if(scc[i])continue;//if scc was constructed, continue
dfs(i);
}
//数组重新使用
memset(fvis,0,sizeof(fvis));
memset(st,0,sizeof(st));
vector<int>dpedge[scc_index+1];
vector<int>::iterator it;
int ans=0;
//rebuilt graph for dp
for(int i=1;i<=n;i++)
{
fvis[scc[i]]+=v[i],ans=max(ans,fvis[scc[i]]);//标记缩点和
if(save[i].empty())continue;
it=save[i].begin();
for(;it!=save[i].end();it++)
{
if(scc[i]!=scc[*it])dpedge[scc[i]].push_back(scc[*it]),st[scc[*it]]++;
}
}
//st是统计入度的,拓扑,dp
queue<int>line;
for(int i=1;i<=scc_index;i++)
{
if(!st[i])line.push(i);//入度为0的元素入队
}
memset(v,0,sizeof(v));
while(!line.empty())
{
int x=line.front();
line.pop();
v[x]+=fvis[x];//dp
if(dpedge[x].empty())continue;
it=dpedge[x].begin();
for(it=dpedge[x].begin();it!=dpedge[x].end();it++)
{
v[*it]=max(v[*it],v[x]);
st[*it]--;
if(!st[*it])line.push(*it);
}
}
for(int i=1;i<=scc_index;i++)
ans=max(ans,v[i]);
cout<<ans<<endl;
return 0;
}
P4782 【模板】2-SAT 问题
#include<iostream>
#include<cstring>
#include<vector>
#include<cstdio>
#include<algorithm>
using namespace std;
#define maxn 1000005
#define re register
inline int read()
{
re int t=0;
re char v=getchar();
while(v<'0')v=getchar();
while(v>='0')
{
t=(t<<3)+(t<<1)+v-48;
v=getchar();
}
return t;
}
vector<int>save[maxn<<1];
int m,n,x,y,x1,y1;
int src[maxn<<1],fvis[maxn<<1],scc[maxn<<1],st[maxn<<1];
int cnt,scc_index,curtime;
bool check[maxn<<1];
void dfs(int pos)
{
src[pos]=fvis[pos]=++curtime;
st[++cnt]=pos;
check[pos]=1;
for(vector<int>::iterator it=save[pos].begin();it!=save[pos].end();it++)
{
if(check[*it]){src[pos]=min(src[pos],src[*it]);continue;}
if(!src[*it])dfs(*it),src[pos]=min(src[pos],src[*it]);
}
if(src[pos]==fvis[pos])
{
while(st[cnt]!=pos)
scc[st[cnt]]=scc_index,check[st[cnt]]=0,cnt--;
scc[st[cnt]]=scc_index,check[st[cnt]]=0,cnt--;scc_index++;
}
return;
}
int main()
{
cin.tie(0);cout.tie(0);
ios_base::sync_with_stdio(false);
n=read(),m=read();
memset(check,0,sizeof(check));
memset(scc,0,sizeof(scc));
curtime=0,scc_index=1;
for(int i=0;i<m;i++)
{
//save edges
x=read(),x1=read(),y=read(),y1=read();
save[x+n*(x1&1)].push_back(y+n*(y1^1));
save[y+n*(y1&1)].push_back(x+n*(x1^1));
//这里用了位运算让存边简洁很多
}
for(int i=1;i<=(n<<1);i++)
{
cnt=0;
if(scc[i])continue;
dfs(i);
}
for(int i=1;i<=n;i++)
{
if(scc[i]==scc[i+n])
{
cout<<"IMPOSSIBLE"<<endl;
return 0;
}
}
cout<<"POSSIBLE"<<endl;
for(int i=1;i<=n;i++)//比较同一元素拓扑序
{
cout<<(scc[i]<scc[i+n])<<" ";
}
cout<<endl;
return 0;
}
洛谷P4171 [JSOI2010]满汉全席 2-Sat
#include<iostream>
#include<cstring>
#include<vector>
#include<cstdio>
#include<algorithm>
using namespace std;
#define INF 1e10+5
#define maxn 3005
#define re register
inline int read()
{
re int t=0;
re char v=getchar();
while(v<'0')v=getchar();
while(v>='0')
{
t=(t<<3)+(t<<1)+v-48;
v=getchar();
}
return t;
}
vector<int>save[maxn<<1];
int m,n,x,y,x1,y1;
char a,b;
int src[maxn<<1],fvis[maxn<<1],scc[maxn<<1],st[maxn<<1];
int cnt,scc_index,curtime;
bool check[maxn<<1];
void dfs(int pos)
{
src[pos]=fvis[pos]=++curtime;
st[++cnt]=pos;
check[pos]=1;
for(vector<int>::iterator it=save[pos].begin();it!=save[pos].end();it++)
{
if(check[*it]){src[pos]=min(src[pos],src[*it]);continue;}
if(!src[*it])dfs(*it),src[pos]=min(src[pos],src[*it]);
}
if(src[pos]==fvis[pos])
{
while(st[cnt]!=pos)
scc[st[cnt]]=scc_index,check[st[cnt]]=0,cnt--;
scc[st[cnt]]=scc_index,check[st[cnt]]=0,cnt--;scc_index++;
}
return;
}
void solve()
{
memset(check,0,sizeof(check));
memset(scc,0,sizeof(scc));
memset(src,0,sizeof(src));
memset(fvis,0,sizeof(fvis));
n=read(),m=read();
curtime=0,scc_index=1;
for(int i=1;i<=(maxn<<1);i++)
save[i].clear();
for(int i=1;i<=m;i++)
{
cin>>a>>x>>b>>y;
if(a=='m')x1=0;
else x1=1;
if(b=='m')y1=0;
else y1=1;
save[x+n*(x1&1)].push_back(y+n*(y1^1));
save[y+n*(y1&1)].push_back(x+n*(x1^1));
}
for(int i=1;i<=(n<<1);i++)
{
cnt=0;
if(scc[i])continue;
dfs(i);
}
for(int i=1;i<=n;i++)
{
if(scc[i]==scc[i+n])
{
cout<<"BAD"<<'\n';
return;
}
}
cout<<"GOOD"<<'\n';
}
int main()
{
int t;
t=read();
while(t--)solve();
return 0;
}





