Manacher(马拉车算法)
Manacher#
部分资料来自:https://blog.csdn.net/XzzF1024/article/details/80150516?ops_request_misc=&request_id=&biz_id=&utm_source=distribute.pc_search_result.none-task
https://blog.csdn.net/dyx404514/article/details/42061017
题型##
给定一个字符串
求最长回文字符子串,注意是最长子串,不是最长子序列!!
如:s="abbacbca",最长回文子串为 "acbca",长度为5;
如果用暴力的算法,枚举对称轴,向两边延伸,复杂度高达On2
预处理###
回文串 分为 奇回文串(如"acbca") 和 偶回文串(如 "abba")
那么算法为了解决奇偶问题
它选择将所有空隙填上无关字符'#'
使得上面的两个串变成"#a#c#b#c#a#" 和 "#a#b#b#a#"
这样他们的长度恒定是奇数,便于下面的处理
还有一点,为了避免更新越界,我们在字符串的前增加一个特殊字符,比如说‘$’,所以算法中字符串是从1开始的。
算法部分##
1.len[i]数组
用来储存以i为中心的最长字符串的左右半径(包括自己)
如下面:
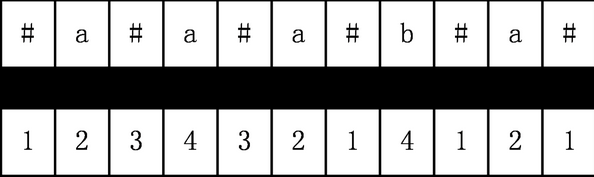
len数组有一个性质,那就是Len[i]-1就是该回文子串在原字符串S中的长度
2.len数组的计算###
从左往右依次计算Len[i]
显然当计算Len[i]时,Lenj已经计算完毕。
设P为之前计算中最长回文子串的右端点的最大值,并且设取得这个最大值的位置为Po,
我们现在研究i,取i相对于po的对称位置,设为j,分两种情况:
第一种情况:i<=P####
1)如果Len[j]<P-i,即所求区段已被大区段包含,如下图:
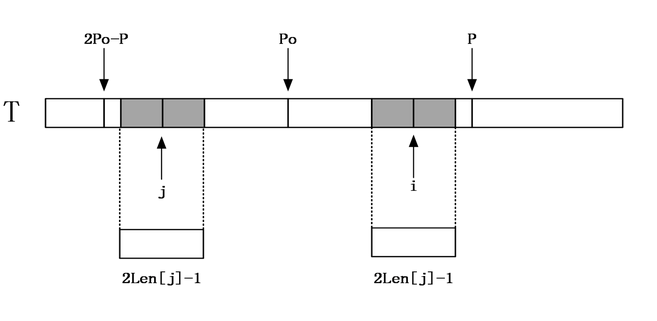
那么说明以j为中心的回文串一定在以Po为中心的回文串的内部,且j和i关于位置po对称,由回文串的定义可知,一个回文串反过来还是一个回文串,所以以i为中心的回文串的长度至少和以j为中心的回文串一样,即Len[i]>=Len[j]。因为Len[j]<P-i,所以说i+Len[j]<P。
由对称性可知Len[i]=Len[j]。
2)如果Len[j]=<P-i,即所求区段有部分不在大区段内,如下图:
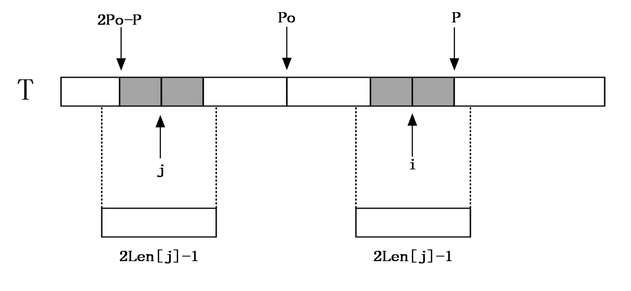
由对称性,说明以i为中心的回文串可能会延伸到P之外,而大于P的部分我们还没有进行匹配,所以要从P+1位置开始一个一个进行匹配,直到发生失配,从而更新P和对应的po以及Len[i]。
第二种情况:i>P####
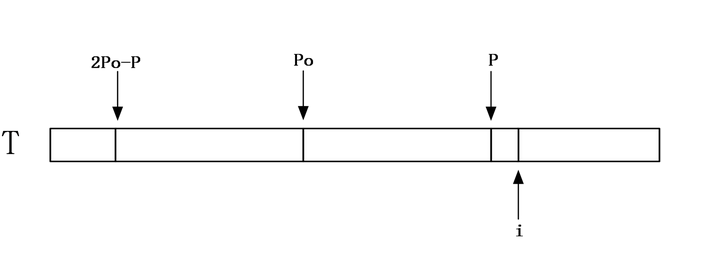
如果i比P还要大,说明对于中点为i的回文串还一点都没有匹配,这个时候,就只能老老实实地一个一个匹配了,匹配完成后要更新P的位置和对应的P、o以及Len[i]。
上面的情况枚举的比较详细,但是实际写代码,可以把第一种的第2类分别拆成两部分,合并另为两种情况里面去,这要可以使得代码量和可读性大大提升
洛谷板子P3805##
#include<iostream>
#include<cstring>
#include<string>
using namespace std;
#define maxn 10000005
typedef long long ll;
int main()
{
string s;
cin>>s;
char a[maxn<<1];
int radius[maxn<<1];
int mid=0,r=0,ans=0;//r是当前所有回文串中右端能到的最大位置,mid是它对应的中心
a[0]='$',a[1]='#';
for(int i=1;i<=s.size();i++)
a[i<<1]=s[i-1],a[(i<<1)+1]='#';//原字符串aaaa...,存成$#a#..#a#
for(int i=1;i<=2*s.size();i++)
{
radius[i]=0;//初始化
if(i<=r)radius[i]=min(r-i+1,radius[(mid<<1)-i]);//计算第一,二类情况中可能覆盖了的部分
while(a[i-radius[i]]==a[i+radius[i]])radius[i]++;//枚举第二,三类中逾越部分,a[0]='$'就是为了这里方便
if(radius[i]+i-1>=r)mid=i,r=radius[i]+i-1;//更新右标签,mid改为当前位置
ans=max(ans,radius[i]);//更新最大值
}
cout<<ans-1<<endl;
return 0;
}
CF Global Round 7 D2##
有一说一,打这场晚上我突然脑袋一热来看马拉车,结果当晚cf直接就来了...
题意:给定一个字符串,现在让你取它的一个前缀和后缀,拼起来使得是回文串,求最长的方案,并输出之,有多组数据
思路:这个就是马拉车的经典使用了
首先前后只要是一样的就能拿出来
接下来的问题无非就是选取剩下这个子串中的最长前缀或者最长后缀,使得它是回文串
这个就是manacher的功能了
后缀逆序就是前缀了,而你更新最大回文子串要保证他是前缀,无非就要保证radius要等于当前下标即可
值得一提的是,因为多组数据,然后没做清空数组处理,很容易导致越界访问,所以要格外注意
AC:
#include<iostream>
#include<cstring>
#include<vector>
#include<string>
#include<algorithm>
using namespace std;
#define INF 1e10+5
#define maxn 1000005
typedef long long ll;
char a[maxn<<1];
int radius[maxn<<1];
string check(string aa,bool re)
{
if(!re)reverse(aa.begin(),aa.end());
string s=aa;
int mid=0,r=0,ans=0;
a[0]='$',a[1]='#';
for(int i=1;i<=s.size();i++)
a[i<<1]=s[i-1],a[(i<<1)+1]='#';
for(int i=1;i<=2*s.size();i++)
{
radius[i]=0;
if(i<=r)radius[i]=min(r-i+1,radius[(mid<<1)-i]);
while(a[i-radius[i]]==a[i+radius[i]]&&i+radius[i]<=2*s.size()+1) radius[i]++;
if(radius[i]+i-1>=r)mid=i,r=radius[i]+i-1;
if(radius[i]==i)ans=max(ans,radius[i]);
}
aa=s.substr(0,ans-1);
if(!re)reverse(aa.begin(),aa.end());
return aa;
}
void solve()
{
string s;
vector<char>curline;
cin>>s;
int num=0;
for(int i=0;i<s.size()/2;i++)
{
if(s[i]==s[s.size()-1-i])curline.push_back(s[i]),num++;
else break;
}
string s1=check(s.substr(num,s.size()-2*num),1);
string s2=check(s.substr(num,s.size()-2*num),0);
if(s1.size()<s2.size())s1=s2;
vector<char>::iterator it;
for(it=curline.begin();it!=curline.end();it++)
cout<<*it;
cout<<s1;
for(it=curline.end()-1;it!=curline.begin()-1;it--)
cout<<*it;
cout<<endl;
}
int main()
{
int t;
cin>>t;
for(int i=0;i<t;i++)
{
solve();
}
return 0;
}




