全局平衡二叉树 (GBST) 小记

全局平衡二叉树 (GBST) 小记

以下全局平衡二叉树简称 \(\text{GBST(Globel Balanced Search Tree)}\)。

我认识的大多数人，对 \(\text{GBST}\) 的理解基本上都是 静态 \(\text{LCT}\)，或者静态 \(\text{Top Tree}\)，不过我对 \(\text{LCT}\) 的理解可能还差一点，所以我不打算从阉割 \(\text{LCT}\) 的角度来讲解。

于是下文基本上是从树剖优化的角度讲解。

---

考虑一个经典的树上问题，\(n\) 个结点，点有点权，\(q\) 次操作，操作有两种：

• 给定 \(x, y, k\)，将 \(x\) 到 \(y\) 路径上的点权值 \(+k\)。
• 给定 \(x, y\)，求 \(x\) 到 \(y\) 路径上所有点的权值之和。

首先经典的可以将问题差分，变成前缀链加和前缀链查询。于是下面我们都默认链是树上的前缀，即一条 \(x\) 到根的路径。

对原树重链剖分，注意到无论是修改还是查询，都作用在重链的一段前缀上。这给了我们一些操作的空间。

考虑对于每条重链分别维护线段树，而不是简单的用 \(\text{dfs}\) 序拍平成序列问题，但这样只是常数小一点（真的小了吗？），对于单条重链上做修改/查询的时间复杂度还是 \(O(\log n)\) 的。

我们发现时间复杂度优化不了，本质上的原因的每条重链是独立的。我们考虑用一些数据结构将树剖的 \(\log\) 和线段树的 \(\text{log}\) 联系起来。

具体而言，我们对于重链用一棵二叉搜索树维护。由于二叉搜索树的真实顺序是其中序遍历，画画图就能知道求的是什么。考虑 \(x\) 到 \(x\) 所在重链链顶的贡献，拿出对于每条树边 \(u \rightarrow v\)，如果 \(u\) 是 \(v\) 右儿子则将 \(u\) 加入集合 \(s\)，特别的 \(x\) 也在 \(s\) 中。会被操作覆盖的点是 \(s\) 中所有点和其左子树的并，这样可以做到一个看似 \(O(1)\) 修改/查询。

但是如果真的建一个完全二叉树，那复杂度又回去了。因为对于一条重链，还是会在该重链对应的二叉树上条 \(O(\log n)\) 步。

于是考虑构造一个类似于 每跳一条边，子树大小翻倍的结构。我们发现轻边已经满足这个要求，要是完全二叉树上的边也满足这个要求，不难想到建二叉树时不取中点为根（取中点就是完全二叉树），而取关于子树大小的带权中点即可。

但是带权中点总会向一边倾斜，所以最坏情况下要条两条边才能使子树大小翻倍。也就是说最坏情况下，\(\text{GBST}\) 上一个点的深度是 \(2 \log n\)。可能又更好的分析/构造方法得到类似 深度不超过 \(\log n + O(1)\) 的结论，不过它已经足够优秀，我就懒得想了。

---

下面是例题：

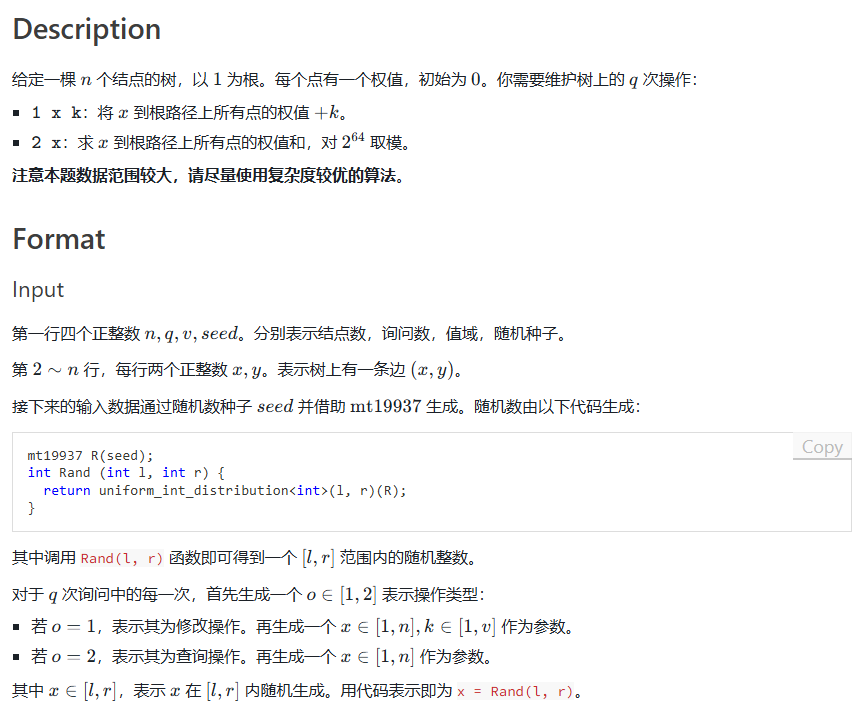
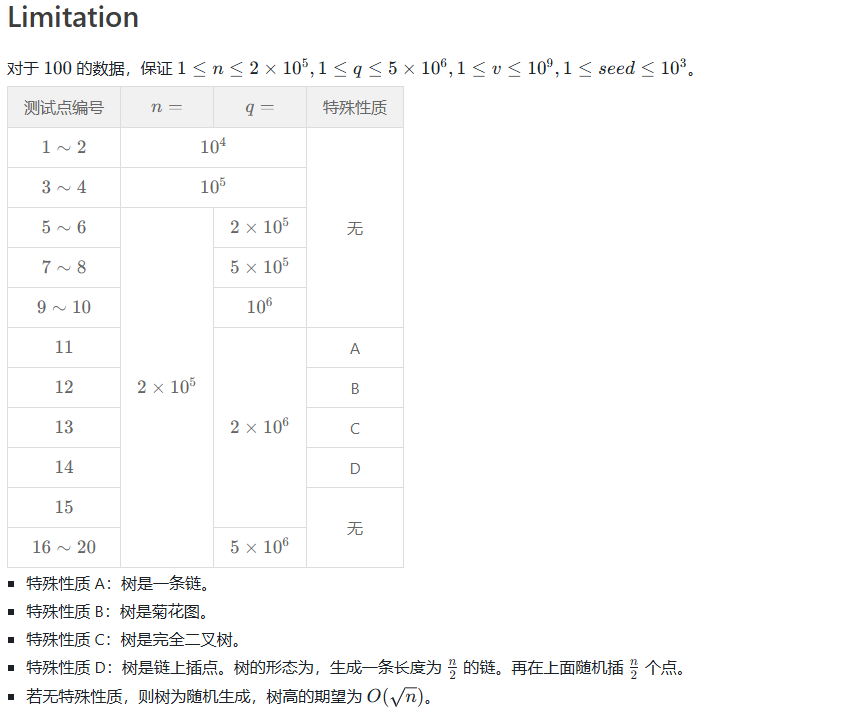
代码：

#include <iostream> 
#include <vector>
#include <random>
#include <algorithm>

using namespace std;
using uLL = unsigned long long;

const int N = 2e5 + 5; 

int n, q, v, seed;
vector<int> e[N];
int fa[N], siz[N], wson[N];
int lc[N], rc[N], ss[N];
uLL val[N], sum[N], tag[N];
mt19937 R;

bool Get_which (int x) {
  return x == lc[fa[x]] ? 0 : (x == rc[fa[x]] ? 1 : -1);
}

int Rand (int l, int r) {
  return uniform_int_distribution<int>(l, r)(R);
} 

void Init (int u, int r) {
  if (r) e[u].erase(find(e[u].begin(), e[u].end(), r));
  siz[u] = 1; 
  for (auto v : e[u]) {
    if (v == r) continue;
    Init(v, u);
    siz[u] += siz[v];
    if (siz[v] > siz[wson[u]]) {
      wson[u] = v; 
    }
  }
}

int Build (vector<int>::iterator itl, vector<int>::iterator itr) {
  if (itl == itr) return 0; 
  int bot = siz[*prev(itr)], top = siz[*itl] - bot;
  auto mid = upper_bound(itl, itr, top / 2, [&](int half, int x) -> bool {
    return siz[x] - bot <= half;
  });
  int u = *mid;
  lc[u] = Build(itl, mid), rc[u] = Build(mid + 1, itr);
  fa[lc[u]] = fa[rc[u]] = u, ss[u] = ss[lc[u]] + ss[rc[u]] + 1;
  return u; 
}

int Divide (int u) {
  vector<int> lis;
  for (int s = u; s; s = wson[s]) {
    lis.push_back(s);
    for (auto v : e[s]) {
      if (v != wson[s])
        fa[Divide(v)] = s;
    }

  }
  return Build(lis.begin(), lis.end());
}

void Node_add (int x, uLL y) {
  val[x] += y, sum[x] += y * ss[x], tag[x] += y; 
}

void Pushdown (int x) {
  if (tag[x]) {
    if (lc[x]) Node_add(lc[x], tag[x]);
    if (rc[x]) Node_add(rc[x], tag[x]);
    tag[x] = 0; 
  }
}

void Pushup (int x) {
  sum[x] = sum[lc[x]] + sum[rc[x]] + val[x];
}

void Add (int x, int y, int whi = -1) {
  if (fa[x]) {
    Add(fa[x], y, Get_which(x));
  }
  Pushdown(x);
  if (whi != 0) {
    val[x] += y, sum[x] += y; 
    if (lc[x]) Node_add(lc[x], y);
  }
  if (whi == -1) {
    for (int i = x; i; i = fa[i]) {
      Pushup(i);
      if (Get_which(i) == -1) break;
    }
  }
}

uLL Query (int x, int whi = -1) {
  uLL res = 0; 
  if (fa[x]) {
    res = Query(fa[x], Get_which(x));
  }
  Pushdown(x);
  if (whi != 0) {
    res += val[x] + sum[lc[x]];
  }
  return res;
}

int main () {
  cin.tie(0)->sync_with_stdio(0);
  cin >> n >> q >> v >> seed, R = mt19937(seed); 
  for (int i = 1, x, y; i < n; ++i) {
    cin >> x >> y; 
    e[x].push_back(y);
    e[y].push_back(x);
  }
  Init(1, 0), Divide(1); 
  uLL ans = 0; 
  for (int i = 1, o, x, y; i <= q; ++i) {
    o = Rand(1, 2), x = Rand(1, n); 
    if (o == 1) {
      y = Rand(1, v);
      Add(x, y);
    }
    else {
      uLL ret = Query(x);
      ans ^= i * ret;
    }
  }
  cout << ans << '\n';
  return 0; 
}

---

下面是效率比较，以上面的例题为例（\(n = 2 \times 10^5, q = 5 \times 10^6\)）：

树的形态	树剖+线段树	\(\text{GBST}\)	暴力跳
随机树（深度为 \(O(\sqrt n)\)）	\(\text{3.9s}\)	\(\text{1.8s}\)	\(\text{3.0s}\)
链	\(\text{1.6s}\)	\(\text{2.5s}\)	\(\ge \text{100.0s}\)
菊花	\(\text{1.6s}\)	\(\text{0.4s}\)	\(\text{0.3s}\)
完全二叉树	\(\text{6.8s}\)	\(\text{1.5s}\)	\(\text{0.6s}\)
链上插点	\(\text{2.1s}\)	\(\text{2.3s}\)	\(\ge \text{100.0s}\)

然后 \(\text{GBST}\) 期望跳的边数是 \(13.6663502‬\)，基本上和 \(2 \log n\) 比较接近，因为是期望，所以有个 \(\frac{1}{3} \sim \frac{1}{2}\) 的常数是正常的。

这里暴力跳仅作为对照，参考意义不大。为什么 \(\text{GBST}\) 理论复杂度比树剖少个 \(\log n\)，实际表现却没有那么优秀？主要原因有以下几个：

• 树剖本身很难卡满，这里的难卡满指的是重链条数，因为你拍成 \(\text{dfs}\) 序做的话实际上具体查询的区间是什么对时间复杂度影响是不大的。

• 我写的 \(\text{GBST}\) 没有标记永久化，那么每次全部 \(\text{pushdown}\) 一遍常数其实是挺大的。

• 这题 \(n\) 较小而 \(q\) 较大，这是为了减小输入量。但是 \(\text{GBST}\) 和树剖的复杂度差距是靠 \(n\) 拉开的，所以这道题其实没出好。

并且 \(\text{GBST}\) 还有一个缺陷。前面我们讨论的都是默认差分后的情况，但任意路径的前缀修改/求和需要差分成四条前缀链，但树剖可以自然的处理掉，所以如果真要差分的话 \(\text{GBST}\) 可能还要带一个两倍左右的常数。

当然你可以用一个类似树剖的写法，而不去差分成前缀链。那么这样的问题是在修改的两个点 \(x\) 和 \(y\) 相遇时，相当于要做一个任意区间修改/查询，好在你只需做一次，那么可以接受单次 \(O(\log n)\) 的时间复杂度。还是在二叉搜索树上暴力跳，做一些分讨即可。

所以这样理论上树剖能做的问题，\(\text{GBST}\) 都是能做的，包括像链上 \(\min\) 这样的不可差分问题。不过它最经典的应用应该还是优化 \(\text{ddp}\)，因为它本身就是前缀，又没有懒标记之类的东西，所以写起来非常方便。