einops 学习笔记：基础篇

参考：

https://einops.rocks/1-einops-basics/

einops（Einstein Operations）提供了一种语法来便捷地操纵张量。einops 支持大多数张量库（当然包括 numpy 和 pytorch）。einops 针对所有张量库的语法都完全一致。einops 不会影响反向传播的正常进行。这些特性意味着 einops 可以和现有的深度学习框架和代码库无缝集成。

本文的大部分内容是对上述官方文档的翻译，添加了一些自己的理解，调整了一些小节的顺序。

如何运行代码

如果要跟着下面的步骤实操，需要先下载 test_images.npy 文件（可以从 einops 的 GitHub 仓库下载到），再将以下代码粘贴进一个 util.py 文件：

import numpy as np

from PIL.Image import fromarray
from IPython import get_ipython


def display_np_arrays_as_images():
    def np_to_png(a):
        if 2 <= len(a.shape) <= 3:
            return fromarray(np.array(np.clip(a, 0, 1) * 255, dtype='uint8'))._repr_png_()
        else:
            return fromarray(np.zeros([1, 1], dtype='uint8'))._repr_png_()

    def np_to_text(obj, p, cycle):
        if len(obj.shape) < 2:
            print(repr(obj))
        if 2 <= len(obj.shape) <= 3:
            pass
        else:
            print('<array of shape {}>'.format(obj.shape))

    get_ipython().display_formatter.formatters['image/png'].for_type(np.ndarray, np_to_png)
    get_ipython().display_formatter.formatters['text/plain'].for_type(np.ndarray, np_to_text)


from IPython.display import display_html

_style_inline = """<style>
.einops-answer {
    color: transparent;
    padding: 5px 15px;
    background-color: #def;
}
.einops-answer:hover { color: blue; } 
</style>
"""


def guess(x):
    display_html(
        _style_inline
        + "<h4>Answer is: <span class='einops-answer'>{x}</span> (hover to see)</h4>".format(x=tuple(x)),
        raw=True)

在与 util.py 同级的目录中创建 Notebook，然后先执行以下代码段：

from utils import display_np_arrays_as_images
display_np_arrays_as_images()

这会将 numpy 的数组转换成图片显示出来。

准备

载入一些图片：

ims = numpy.load('./resources/test_images.npy', allow_pickle=False)
# 有 6 张 96x96、带有 3 个色彩通道的图片，打包进同一个张量
print(ims.shape, ims.dtype)     # (6, 96, 96, 3) float64

这是 ims[0]：

这是 ims[1]：

`rearrange` 重排

rearrange 用于重新排列张量的各个 axis。

from einops import rearrange
# 交换 height 和 width 的顺序
rearrange(ims[0], 'h w c -> w h c')

composition

将加载的张量转换为一整张图片：

rearrange(ims, 'b h w c -> (b h) w c')

rearrange(ims, 'b h w c -> h (b w) c')

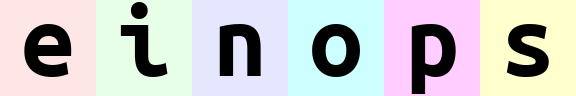
# [6, 96, 96, 3] -> [96, (6 * 96), 3]
rearrange(ims, 'b h w c -> h (b w) c').shape    # (96, 576, 3)

可以 compose 多于一个 axis：

rearrange(ims, 'b h w c -> (b h w c)').shape    # (165888,)

decomposition

decomposition 是 composition 的逆操作。

# 指定 b1=2，则 b2 的值将自动推算(结果为6/2=3)
rearrange(ims, '(b1 b2) h w c -> b1 b2 h w c ', b1=2).shape     # (2, 3, 96, 96, 3)

可以将 composition 和 decomposition 结合：

rearrange(ims, '(b1 b2) h w c -> (b1 h) (b2 w) c ', b1=2)

另一个例子：

rearrange(ims, '(b1 b2) h w c -> (b2 h) (b1 w) c ', b1=2)

下面的操作将每张图的高度加倍，宽度减半，故名为 width-to-height 操作。

rearrange(ims, 'b h (w w2) c -> (h w2) (b w) c', w2=2)

横板的 height-to-width 操作：

rearrange(ims, 'b (h h2) w c -> h (b w h2) c', h2=2)

竖版的 height-to-width 操作：

rearrange(ims, 'b (h h2) w c -> (b h) (w h2) c', h2=2)

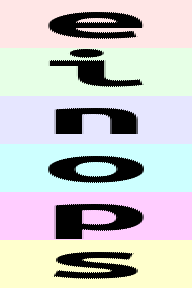
轴的顺序很重要

比较以下两行代码的结果：

rearrange(ims, 'b h w c -> h (b w) c')

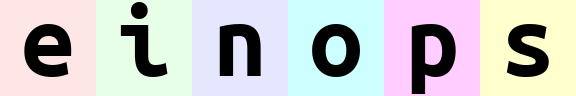
rearrange(ims, 'b h w c -> h (w b) c')

就像一串数字一样，最左侧的数字（最高位）是最重要的。einops 在组合时会先从低位（右侧）排列，排列完低位后再排列高位。对于上面的例子：

(b w) 表示在水平方向上先排列 w（表示每张图的所有水平像素），再排列 b（表示每张图本身）。于是图片会一张一张地排出来。
(w b) 表示在水平方向上先排列 b，再排列 w。于是会先顺序排出e、i、n、o、p、s 各自的第一列像素，然后排第二列，如此重复。

再看一个例子：

rearrange(ims, '(b1 b2) h w c -> h (b1 b2 w) c ', b1=2) # 输出 'einops'
rearrange(ims, '(b1 b2) h w c -> h (b2 b1 w) c ', b1=2) # 输出 'eoipns'

以上两行代码都将 w 放在最右侧，在输出水平方向的像素时，总是排完一张图，再排下一张。不同的是 b1 和 b2 的顺序。解构的模式是 (b1 b2)，其中 b1=2，那么可以想象将原先的 b=6 重排成了一个 \(2\times 3\) 的矩阵：

第一行代码是先排列 b2（因为它在 b1 右边），再排列 b1，而这与前面解构出的顺序是一致的，于是
- 先固定 b1 为第一行，输出该行的所有元素（ein）
- 然后固定 b1 为第二行，输出该行的所有元素（ops）
而第二行代码是先排列 b1，再排列 b2，于是
- 先固定 b2 为第一列，然后输出该列的所有元素（eo）
- 然后固定 b2 为第二列，然后输出该列的所有元素（ip）
- 然后固定 b2 为第三列，然后输出该列的所有元素（ns）

堆叠和拼接张量

einops 还可以处理 list。将 ims 转换为一个 list：

x = list(ims)

此时 x 是一个带有 6 个元素的 list，每个元素是一个 numpy.ndarray，对应一个字母的图片。当用 einops 处理 x 时，输入的第一个维度是 list 本身的维度，对于 x，就是原先的 b。

堆叠张量：

rearrange(x, 'b h w c -> h w c b')
# 等价于
numpy.stack(x, axis=3)

拼接张量：

rearrange(x, 'b h w c -> h (b w) c')
# 等价于
numpy.concatenate(x, axis=1)

增加和删除轴

可以通过在输入中写 1 来减少轴，也可以通过在输出中写 1 来增加轴。

x = rearrange(ims, 'b h w c -> b 1 h w 1 c') # 类似 numpy.expand_dims
print(x.shape)
print(rearrange(x, 'b 1 h w 1 c -> b h w c').shape) # 类似 numpy.squeeze

输出如下：

(6, 1, 96, 96, 1, 3)
(6, 96, 96, 3)

下面的代码将在 h 和 w 方向上分别取 b 和 c 的最大值，形成一个 (6, 1, 1, 3) 的张量：

reduce(ims, 'b h w c -> b () () c', 'max')

`reduce` 缩减

如果要在某个轴的方向上求平均，传统的写法是

x.mean(-1)

但是这种代码可读性不佳。如果缺乏经验，那么我们难以立即知道 -1 指的是哪个轴。

在 einops 中，上面的代码可以写成：

reduce(x, 'b h w c -> b h w', 'mean')

如果某个轴在输入中出现，但在输出中没有出现，那么这个轴就是被执行 reduce 操作的轴。在上面的例子中，轴 c 被执行了求平均值操作。

在 batch 轴上执行求平均值操作：

# 等价于 ims.mean(axis=0)
reduce(ims, 'b h w c -> h w c', 'mean')
# 也等价于 reduce(ims, 'b h w c -> h w', 'mean')

有如下几种 reduce 操作：

mean 求平均值
min 求最小值
max 求最大值
sum 求和
prod 求乘积

einops 的语法允许我们设计池化操作。下面的代码执行了 \(2\times 2\) 平均池化：

reduce(ims, 'b (h h2) (w w2) c -> h (b w) c', 'mean', h2=2, w2=2)

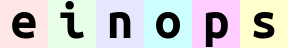
当然，这张图片的长和宽都减半了。

\(2\times 2\) 最大池化：

reduce(ims, 'b (h h2) (w w2) c -> h (b w) c', 'max', h2=2, w2=2)

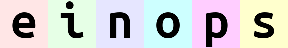
相比平均池化，最大池化没有那么平滑。

另一个例子：

reduce(ims, '(b1 b2) h w c -> (b2 h) (b1 w)', 'mean', b1=2)

`repeat` 重复

在 w 轴的方向上重复：

repeat(ims[0], 'h w c -> h (repeat w) c', repeat=3)

像 rearrange 一样，repeat 同样对轴的顺序敏感。你可以通过改变括号内的轴的顺序来将一个像素重复三次，而不是将图片整体重复三次：

repeat(ims[0], 'h w c -> h (w repeat) c', repeat=3)

当然也可以在纵向上将一个像素重复三次：

repeat(ims[0], 'h w c -> (h repeat) w c', repeat=3)

同时在 w 和 h 轴的方向上重复：

repeat(ims[0], 'h w c -> (2 h) (2 w) c')

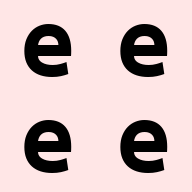
同样，通过调整顺序，可以将一个像素在 h 和 w 的方向上分别重复两次，这有点像 \(2\times 2\) 池化的逆操作。实际上 reduce 和 repeat 可以互相视为逆操作。

repeat(ims[0], 'h w c -> (h 2) (w 2) c')

在一个新的轴上重复：

print(ims[0].shape)     # (96, 96, 3)
repeat(ims[0], 'h w c -> h new_axis w c', new_axis=5).shape     # (96, 5, 96, 3)

新的张量是原先的 (96, 96, 3) 张量在第二个轴上重复了 5 次得到的。

总结

rearrange 不改变张量中元素的总个数。
reduce 在保持基本重排语法不变的同时引入了缩减操作（mean, min, max, sum, prod）
repeat 包括了重复和平铺操作
composition 和 decomposition 是 einops 的基石。它们能够也应该被联合起来使用。

posted @ 2024-02-03 21:23 Eslzzyl 阅读(1148) 评论(0) 编辑收藏举报

刷新页面返回顶部

Eslzzyl