用Rust实现DES加密/解密算法
信息安全技术课程要求实现一下DES算法。对着一份Java代码断断续续抠了几天，算是实现出来了。这里记录一下算法思想和我的Rust实现。
DES 算法解析
概述
https://en.wikipedia.org/wiki/Data_Encryption_Standard
DES是一种对称的分组加密算法，加密和解密使用同一个密钥，计算过程将数据分成长为64位的分组。
DES通过一个原始密钥计算出一组共16个子密钥，然后分别提供给主循环的16轮迭代进行处理。
DES的加密和解密过程高度相似，同一份代码不进行过多的修改即可同时实现加密和解密。
子密钥生成
子密钥生成是DES算法中相对独立的部分。这个部分将一个原始密钥进行处理，生成16个子密钥，每个子密钥48位长。
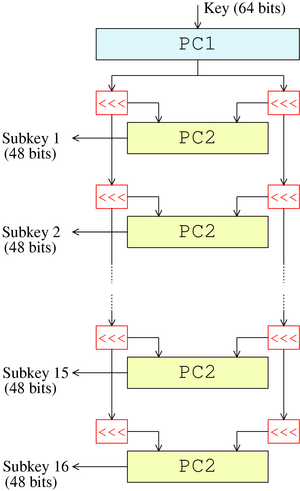
如图所示，原始的64位密钥首先通过PC1置换（下面介绍），得到一个56位的序列（其中的8位被舍弃）。然后分成高低两部分，每部分各28位；之后进行16轮循环，每轮产生一个子密钥。
在每轮循环中，密钥的高低两部分分别循环左移1位或2位。每轮循环移动的位数不同，但有一个固定的表来指出：
| 循环轮次 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 左移位数 | 1 | 1 | 2 | 2 | 2 | 2 | 2 | 2 | 1 | 2 | 2 | 2 | 2 | 2 | 2 | 1 |
左移完毕后，高低两部分重新拼接起来（56位）并通过一个PC2置换，得到一个48位的序列（其中的8位被舍弃），就是当前轮次的子密钥。
整体流程
DES算法的整体流程如下：
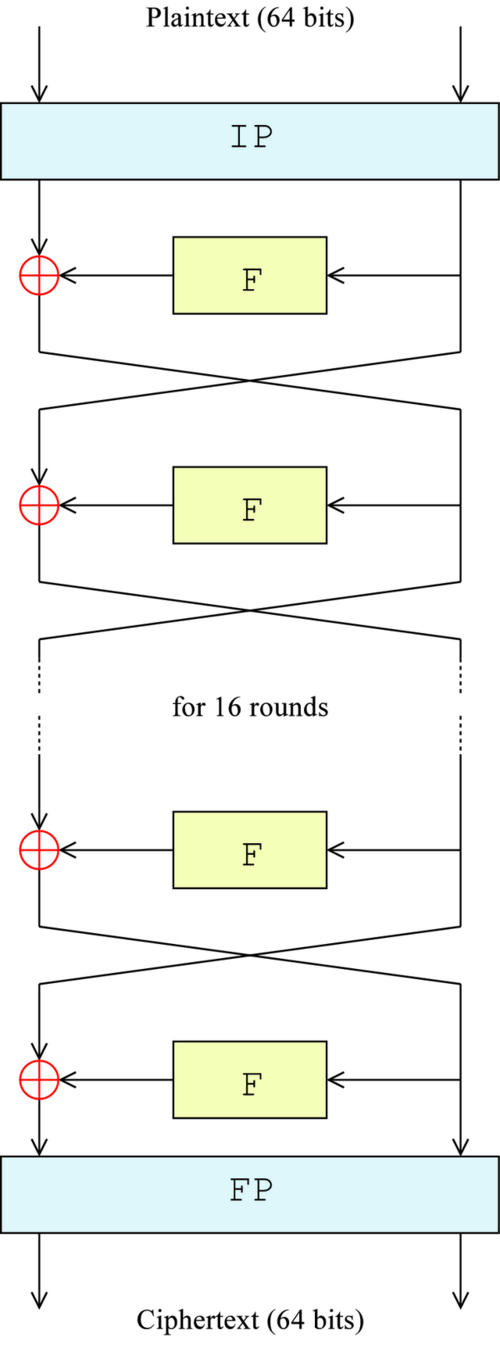
数据分块和补位
前面已经提到，DES是64位长的分组算法，因此原始数据首先分组成长位64位（8字节）的若干个块。如果最后一个块长度不足8字节，则需要补齐。补什么值呢？补的值是需要补的字节数。假设最后一块是3字节，那么需要补5字节，补的值就是5。
这只是DES的众多添补方式的其中之一，不过这种方式比较普及。
16轮迭代计算
数据分组完毕后，每组首先进行一次IP置换（见下文），然后打乱的64位数据分成两半，每半部分各32位。右半部分（\(R_0\)）（低32位）直接赋给下次迭代的左半部分（\(L_1\)），而左半部分（\(L_0\)）则要与一个F函数的结果异或后再赋给下次迭代的右半部分（\(R_1\)）。如此进行16轮迭代，最后一轮迭代中，两部分不交换顺序，而是直接拼接起来，通过FP置换，得到最后的结果。
F是Feistel的缩写。这个函数是DES算法的核心。
F函数
也可以叫Feistel函数或者轮函数。这个函数有两个输入：
- 当前轮次的子密钥，长48位；
- 一段32位的数据。在上面的整体结构中，每次迭代的右半部分（\(R_i\)）被送入F函数。
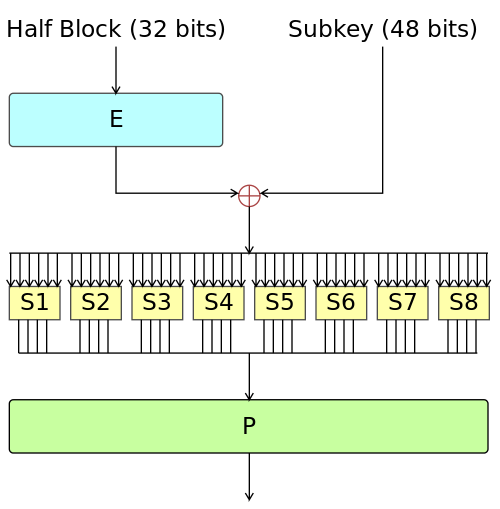
原始32位数据首先通过E扩展置换，扩展到48位，然后和输入的子密钥做一次异或。注意这次异或和整体流程里的异或不一样，也就是说DES的每次迭代有两次异或。
异或的结果（48位）分组通过S盒，得到32位的输出。具体怎么运作的，可以看S盒置换一节。
最后，32位数据通过P置换，结果仍为32位，到此离开F函数。
各种线性置换
DES算法中有许多映射表，以及和这些表对应的置换操作。这些置换大都用于打乱数据的顺序或调整数据的长度，以使加密过程获得更好的效果。
- 在子密钥生成过程中，有
PC1置换和PC2置换。 - 在整体的加密/解密循环中，有
IP置换和FP置换。 - 在Feistel结构中，有
E扩展置换和P置换。还有一个所谓的S盒置换。
上述置换中，只有S盒是非线性的，其他都是线性的。每个置换都有一个固定的映射表，用来指出置换的规则。你可以在此处找到这些映射表。
PC1：64位 -> 56位PC2：56位 -> 48位IP置换、FP置换：64位 -> 64位E扩展置换：32位 -> 48位，这个置换增加了数据的长度，因此叫“扩展”或“扩张”置换。P置换：32位 -> 32位
以IP置换为例，置换表长这样：
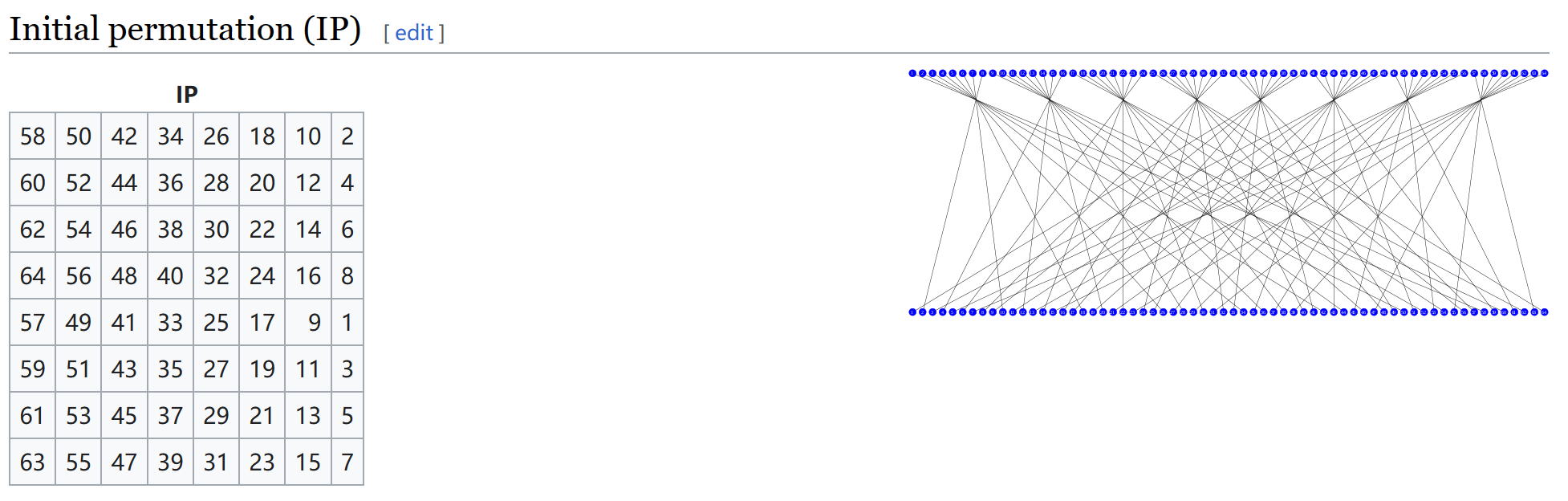
这个表指出，通过IP置换的新数据的第1位是原始数据的第58位，第2位是原始数据的第50位……以此类推。
需要注意，这个置换表中的位数是从1开始数的，但大多数编程语言的索引是从0开始的，因此在编程实现时可能需要将索引减去1。
S盒置换
https://en.wikipedia.org/wiki/S-box 链接里的例子是十分清晰的。
S盒是8个4 * 16的数组，数组的每位是一个不超过16（即不超过4位二进制）的数据。S盒是DES算法中唯一的非线性映射部分，提供了DES最主要的加密性。
在Feistel结构中，48位的数据分成8组，每组（6位）分别通过对应的S盒。
对于某一特定的S盒：
- 输入的6位数据截取首位和末位，拼接成2位（4种可能的组合），作为S盒的行索引。
- 剩余的中间4位数据有16种可能的组合，作为S盒的列索引。
如此这般，6位的数据就可以唯一确定一个S盒中的位置。S盒的每个位置都可用4位二进制表示，8个S盒就形成32位数据，作为S盒步骤的输出。
解密过程
关于DES算法的解密，网上众说纷纭。经过实践，DES算法的解密过程和加密过程仅有以下不同：
- 解密过程的16轮迭代中，子密钥要逆序给出。
- 解密计算结束后，需要将加密时添补的字节（如果有）截掉。
除此之外，算法无需作任何改动。密钥本身也不需要reverse，但是子密钥应该逆序给出。
Rust 实现
下面给出我的Rust实现。写得很烂，代码冗杂，效率低下。轻喷。
置换关系的定义
所有的置换都是通过const数组来定义的。
/// 密钥选择置换-1（PC1）
pub const PC1: [usize; 56] = [
57, 49, 41, 33, 25, 17, 9, 1,
58, 50, 42, 34, 26, 18, 10, 2,
59, 51, 43, 35, 27, 19, 11, 3,
60, 52, 44, 36, 63, 55, 47, 39,
31, 23, 15, 7, 62, 54, 46, 38,
30, 22, 14, 6, 61, 53, 45, 37,
29, 21, 13, 5, 28, 20, 12, 4,
];
/// 密钥选择置换-2（PC2）
pub const PC2: [usize; 48] = [
14, 17, 11, 24, 1, 5, 3, 28,
15, 6, 21, 10, 23, 19, 12, 4,
26, 8, 16, 7, 27, 20, 13, 2,
41, 52, 31, 37, 47, 55, 30, 40,
51, 45, 33, 48, 44, 49, 39, 56,
34, 53, 46, 42, 50, 36, 29, 32,
];
/// P置换
pub const P: [usize; 32] = [
16, 7, 20, 21, 29, 12, 28, 17,
1, 15, 23, 26, 5, 18, 31, 10,
2, 8, 24, 14, 32, 27, 3, 9,
19, 13, 30, 6, 22, 11, 4, 25,
];
/// E扩展
pub const E: [usize; 48] = [
32, 1, 2, 3, 4, 5, 4, 5,
6, 7, 8, 9, 8, 9, 10, 11,
12, 13, 12, 13, 14, 15, 16, 17,
16, 17, 18, 19, 20, 21, 20, 21,
22, 23, 24, 25, 24, 25, 26, 27,
28, 29, 28, 29, 30, 31, 32, 1,
];
/// 初始置换
pub const IP: [usize; 64] = [
58, 50, 42, 34, 26, 18, 10, 2,
60, 52, 44, 36, 28, 20, 12, 4,
62, 54, 46, 38, 30, 22, 14, 6,
64, 56, 48, 40, 32, 24, 16, 8,
57, 49, 41, 33, 25, 17, 9, 1,
59, 51, 43, 35, 27, 19, 11, 3,
61, 53, 45, 37, 29, 21, 13, 5,
63, 55, 47, 39, 31, 23, 15, 7,
];
/// 初始逆置换
pub const FP: [usize; 64] = [
40, 8, 48, 16, 56, 24, 64, 32,
39, 7, 47, 15, 55, 23, 63, 31,
38, 6, 46, 14, 54, 22, 62, 30,
37, 5, 45, 13, 53, 21, 61, 29,
36, 4, 44, 12, 52, 20, 60, 28,
35, 3, 43, 11, 51, 19, 59, 27,
34, 2, 42, 10, 50, 18, 58, 26,
33, 1, 41, 9, 49, 17, 57, 25,
];
/// 左移位数表
pub const LFT: [usize; 16] = [
1, 1, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 1,
];
/// S盒
pub const SBOX: [[[u8; 16]; 4]; 8] = [
[
[ 14, 4, 13, 1, 2, 15, 11, 8, 3, 10, 6, 12, 5, 9, 0, 7 ],
[ 0, 15, 7, 4, 14, 2, 13, 1, 10, 6, 12, 11, 9, 5, 3, 8 ],
[ 4, 1, 14, 8, 13, 6, 2, 11, 15, 12, 9, 7, 3, 10, 5, 0 ],
[ 15, 12, 8, 2, 4, 9, 1, 7, 5, 11, 3, 14, 10, 0, 6, 13 ],
],
[
[ 15, 1, 8, 14, 6, 11, 3, 4, 9, 7, 2, 13, 12, 0, 5, 10 ],
[ 3, 13, 4, 7, 15, 2, 8, 14, 12, 0, 1, 10, 6, 9, 11, 5 ],
[ 0, 14, 7, 11, 10, 4, 13, 1, 5, 8, 12, 6, 9, 3, 2, 15 ],
[ 13, 8, 10, 1, 3, 15, 4, 2, 11, 6, 7, 12, 0, 5, 14, 9 ],
],
[
[ 10, 0, 9, 14, 6, 3, 15, 5, 1, 13, 12, 7, 11, 4, 2, 8 ],
[ 13, 7, 0, 9, 3, 4, 6, 10, 2, 8, 5, 14, 12, 11, 15, 1 ],
[ 13, 6, 4, 9, 8, 15, 3, 0, 11, 1, 2, 12, 5, 10, 14, 7 ],
[ 1, 10, 13, 0, 6, 9, 8, 7, 4, 15, 14, 3, 11, 5, 2, 12 ],
],
[
[ 7, 13, 14, 3, 0, 6, 9, 10, 1, 2, 8, 5, 11, 12, 4, 15 ],
[ 13, 8, 11, 5, 6, 15, 0, 3, 4, 7, 2, 12, 1, 10, 14, 9 ],
[ 10, 6, 9, 0, 12, 11, 7, 13, 15, 1, 3, 14, 5, 2, 8, 4 ],
[ 3, 15, 0, 6, 10, 1, 13, 8, 9, 4, 5, 11, 12, 7, 2, 14 ],
],
[
[ 2, 12, 4, 1, 7, 10, 11, 6, 8, 5, 3, 15, 13, 0, 14, 9 ],
[ 14, 11, 2, 12, 4, 7, 13, 1, 5, 0, 15, 10, 3, 9, 8, 6 ],
[ 4, 2, 1, 11, 10, 13, 7, 8, 15, 9, 12, 5, 6, 3, 0, 14 ],
[ 11, 8, 12, 7, 1, 14, 2, 13, 6, 15, 0, 9, 10, 4, 5, 3 ],
],
[
[ 12, 1, 10, 15, 9, 2, 6, 8, 0, 13, 3, 4, 14, 7, 5, 11 ],
[ 10, 15, 4, 2, 7, 12, 9, 5, 6, 1, 13, 14, 0, 11, 3, 8 ],
[ 9, 14, 15, 5, 2, 8, 12, 3, 7, 0, 4, 10, 1, 13, 11, 6 ],
[ 4, 3, 2, 12, 9, 5, 15, 10, 11, 14, 1, 7, 6, 0, 8, 13 ],
],
[
[ 4, 11, 2, 14, 15, 0, 8, 13, 3, 12, 9, 7, 5, 10, 6, 1 ],
[ 13, 0, 11, 7, 4, 9, 1, 10, 14, 3, 5, 12, 2, 15, 8, 6 ],
[ 1, 4, 11, 13, 12, 3, 7, 14, 10, 15, 6, 8, 0, 5, 9, 2 ],
[ 6, 11, 13, 8, 1, 4, 10, 7, 9, 5, 0, 15, 14, 2, 3, 12 ],
],
[
[ 13, 2, 8, 4, 6, 15, 11, 1, 10, 9, 3, 14, 5, 0, 12, 7 ],
[ 1, 15, 13, 8, 10, 3, 7, 4, 12, 5, 6, 11, 0, 14, 9, 2 ],
[ 7, 11, 4, 1, 9, 12, 14, 2, 0, 6, 10, 13, 15, 3, 5, 8 ],
[ 2, 1, 14, 7, 4, 10, 8, 13, 15, 12, 9, 0, 3, 5, 6, 11 ],
],
];
这里面值得说一下的是S盒。根据上面的解析，S盒共有8个，每个S盒有4行、16列。计算时，将原始的48位数据分为8组，每组6位，分别查对应的S盒。
整体结构
数据结构的定义
定义一个Des结构体，然后为其实现加密/解密功能。
/// 控制数据的DES加密/解密
#[derive(PartialEq)]
pub enum DESMode {
Encrypt,
Decrypt,
}
pub struct Des {
data: Vec<u64>,
origin_len: usize,
mode: DESMode,
keys: [[u8; 48]; 16],
}
DESMode控制数据的加密/解密，data是一个u64序列，每个u64都是DES算法中的一个计算分组。
origin_len是用于解密恢复的，在加密里没什么用。
keys是16个48位的子密钥。
Des对象的初始化
impl Des {
/// 创建一个DES对象
///
/// 参数：
/// - `key`：密钥
/// - `source`：待加密（解密）的源字节流
/// - `mode`：控制加密/解密
/// - `origin_len`：数据的长度
pub fn from(key: &str, source: &[u8], mode: DESMode, origin_len: usize) -> Self {
let len = source.len(); // 原始字节流长度
let g = len / 8;
let r = 8 - (len - g * 8);
let mut data = Vec::<u8>::new();
// 如果字节流长度不是8的整数倍，则需补齐。补的值是需要补的位数。
if r < 8 {
data.resize(len + r, r.try_into().unwrap()); // 情况填入的值不会被完全覆盖，必须填入r
} else {
data.resize(len, 0); // 填充什么值都可以，之后会被完全覆盖
}
data[..len].copy_from_slice(&source);
// 每8个字节一组形成Vec<u64>
let result: Vec<u64> = data
.chunks_exact(8)
.map(|chunk| u64::from_le_bytes(chunk.try_into().unwrap()))
.collect();
// 生成子密钥
let keys = Self::generate_keys(key);
Self {
data: result,
origin_len: match mode {
DESMode::Encrypt => len,
DESMode::Decrypt => origin_len,
},
mode,
keys,
}
}
}
Des对象输出为字节流
impl Des {
/// 将内部的`data`类型导出为字节流
pub fn as_bytes(&self) -> Vec<u8> {
let mut bytes = vec![];
for u64_val in &self.data {
bytes.extend(u64_val.to_be_bytes().iter());
}
// 如果是加密，则bytes必定是8的整数倍，可以无脑返回
// 如果是解密，则必须截掉加密时添补的字节
match self.mode {
DESMode::Encrypt => bytes,
DESMode::Decrypt => bytes[0..self.origin_len].to_vec()
}
}
}
注意这里针对解密的情况处理了字节流尾部的添补字节。如果不截掉添补字节，在转换回原始格式时很可能会出问题。
生成子密钥
子密钥的生成是一个相对独立的过程。
impl Des {
/// 生成16个子密钥
///
/// 参数：
/// - `key`：输入的密钥
///
/// 返回：
/// - 16个子密钥，每个长度为48位。每个`u8`保存一个二进制位。
fn generate_keys(key: &str) -> [[u8; 48]; 16] {
let mut key_string = key.to_string();
// 若长度不够8字节，则扩展，直至长度大于8
while key_string.len() < 8 {
key_string = key_string.repeat(1);
}
let key_bytes = &key_string.as_bytes()[0..8];
let mut bits = vec![0; 64];
for i in 0..8 {
let temp = key_bytes[i] & 0xFF;
let k_str = format!("{:08b}", temp);
for j in 0..8 {
bits[i * 8 + j] = match k_str.chars().nth(j).unwrap() as u8 {
48 => 0,
49 => 1,
_ => panic!("To bit error!"),
};
}
}
let mut new_bits = vec![0; 56];
// 完成PC1映射
for (i, &index) in PC1.iter().enumerate() {
new_bits[i] = bits[index - 1];
}
let mut l = new_bits[..28].to_vec();
let mut r = new_bits[28..].to_vec();
let mut keys = [[0; 48]; 16];
for i in 0..16 {
// 记录当前轮次左移位数
let lft_count = LFT[i];
// 循环左移
l.rotate_left(lft_count);
r.rotate_left(lft_count);
let temp = [l.clone(), r.clone()].concat();
assert_eq!(temp.len(), 56);
let mut out = vec![0; 48];
// 完成PC2映射
for (i, &index) in PC2.iter().enumerate() {
out[i] = temp[index - 1];
}
// 导出当前轮次子密钥
keys[i] = out.try_into().unwrap();
}
keys
}
}
注意做PC1映射和PC2映射的时候，不要忘记减1的操作。在映射表里，位的顺序是从1开始的，而在数组索引里是从0开始的。
解释一下常见的format!宏。format!宏将参数列表中的数据格式化为一个String。本程序中用到的format!宏均用于将u32或u64数据展开成包含二进制位的String，如果必要还可以搭配下面要介绍的代码段，进一步转换成[u8; _]或Vec<u8>。
{:b}表示转换成二进制序列。{:32b}表示转换成长为32位的二进制序列，不足32位的部分（高位）用空格对齐。{:032b}表示转换成长为32位的二进制序列，不足32位的部分（高位）用0补齐。
另外解释一下下面这个代码段：
for i in 0..64 {
bits[i] = match k_str.chars().nth(i).unwrap() as u8 {
48 => 0,
49 => 1,
_ => panic!("To bit error!"),
};
}
类似的代码段还会在下文中继续出现。这段代码实际上是把k_str这个二进制字符串的每位二进制截取出来放进一个u8数组或者Vec<u8>里。48和49分别是'0'和'1'的ASCII码。
总之是个十分鲁莽的写法。我的直觉告诉我Rust肯定有更优雅的写法……
S盒的实现
/// S盒函数
///
/// 原理：输入是一个48位的数字，将其分割为8块，每块长为6。对于每一块，取第一位和最后一位，形成两位数字，确定
/// S盒的行；剩余4位确定S盒的列，查表得到一个4位的值。为了和分组匹配，S盒也有8个。
fn sbox(data: Vec<u8>) -> Vec<u8> {
// 分块
let chunks: Vec<Vec<u8>> = data
.chunks_exact(6)
.map(|c| c.to_vec())
.collect();
let mut result = vec![0u8; 32];
for i in 0..8 {
let chunk = &chunks[i]; // 取当前chunk
let sbox = SBOX[i]; // 取当前S盒
assert_eq!(chunk.len(), 6);
// 行索引
let row_index = ((chunk[0] << 1) + chunk[5]) as usize;
// 列索引
let column_index = ((chunk[1] << 3) + (chunk[2] << 2) + (chunk[3] << 1) + chunk[4]) as usize;
// 查S盒
let temp = sbox[row_index][column_index];
// 填入结果
result[i * 4] = (temp >> 3) & 1;
result[i * 4 + 1] = (temp >> 2) & 1;
result[i * 4 + 2] = (temp >> 1) & 1;
result[i * 4 + 3] = temp & 1;
}
result
}
将输入的48位数据分成8组，每组6位。对于每一组，取第一位和最后一位，形成4种可能的结果，作为行索引；剩下的4位形成16种可能的结果，作为列索引。6位确定一个S盒中的值，8组确定8个S盒中的值。每个S盒提供4位数据，最后拼接形成32位输出。
弄明白逻辑之后，代码应该是十分易懂的。其实就是取二进制位、重组、查表，然后再次重组二进制位。
轮函数的实现
实际上就是4步
/// 费斯妥结构中的轮函数F。该函数有4个步骤：
/// 1. 使用扩张置换`E`将`data`从32位扩展到48位。
/// 2. 将扩展结果和第`n`个子密钥异或。
/// 3. 将异或结果划分为8个6位的块，分别通过8个对应的S盒。每个S盒输入为6位，输出为4位。最后将8个S盒的结果拼接为32位。
/// 4. 使用`P`置换重组拼接的结果。
///
/// 参数：
/// - `data`：输入的32位数据
/// - `key`：当前轮次子密钥，长度为48，每个`u8`保存一个二进制位
///
/// 返回：
/// - 计算结果
fn round_func(data: u32, key: &[u8; 48]) -> u32 {
// 将u32重组为长为32的Vec<u8>
let mut bits = [0u8; 32];
let temp_string = format!("{:032b}", data);
for i in 0..32 {
bits[i] = match temp_string.chars().nth(i).unwrap() as u8 {
48 => 0,
49 => 1,
_ => panic!("To bit error!"),
};
}
// 执行扩张置换E 和 异或
let mut new_bits = [0u8; 48];
for (i, &index) in E.iter().enumerate() {
new_bits[i] = bits[index - 1] ^ key[i];
}
// 通过S盒
let sbox_result = sbox(new_bits.to_vec());
// 执行P置换
let mut out = [0; 32];
for (i, &index) in P.iter().enumerate() {
out[i] = sbox_result[index - 1];
}
// 导出为u32
let mut result: u32 = 0;
for i in out.iter() {
result = result * 2 + *i as u32;
}
result
}
算法整体实现
先引入一个针对u64做映射的permute_64函数。实际上程序中只有IP和FP两个64位映射用到了这个函数，其他映射都是直接用位索引做的。（又是十分粗暴且不过脑子的nt写法，特别是实现中先拆分位最后又重组起来的操作可谓令人窒息）
/// 进行64位的置换，用于IP和FP置换。输入和输出均为`u64`格式，保存64位数据。
///
/// 参数：
/// - `input`：输入的数据
/// - `table`：映射规则表，实际上可以是`IP`和`FP`的其中一个。
///
/// 返回：
/// - 置换结果
fn permute_64(input: u64, table: &[usize]) -> u64 {
assert_eq!(table.len(), 64); // table的长度一定是64
let temp1 = format!("{:064b}", input);
// dbg!(&temp1);
let mut bits = [0u8; 64];
for i in 0..64 {
bits[i] = match temp1.chars().nth(i).unwrap() as u8 {
48 => 0,
49 => 1,
_ => panic!("To bit error!"),
};
}
let mut output: u64 = 0;
for i in 0..64 {
output = output * 2 + bits[table[i] - 1] as u64;
}
output
}
然后就可以引入主函数了。
impl Des {
/// 完成加/解密的主要函数
pub fn deal(&mut self) {
for chunk in &mut self.data {
// 把chunk拆分成8个u8
let mut temp_string_vec = vec![];
for i in 0..8 {
let byte = (*chunk >> (i * 8)) as u8;
temp_string_vec.push(
format!("{:08b}", byte)
);
}
let temp_string = temp_string_vec.join("");
let mut temp: u64 = 0;
for i in 0..64 {
temp = temp * 2 + match temp_string.chars().nth(i).unwrap() as u64 {
48 => 0,
49 => 1,
_ => panic!("To bit error!"),
};
}
*chunk = temp;
// 执行初始的IP置换
let c = permute_64(*chunk, &IP);
// 左半部分
let mut l = (c >> 32) as u32;
// 右半部分
let mut r = c as u32;
// 进行16轮交叉处理
for i in 0..16 {
match self.mode {
DESMode::Encrypt => {
if i == 15 {
(r, l) = (r, l ^ round_func(r, &self.keys[i]));
} else {
// l直接继承上一轮的r，r则通过上一轮的l和当前轮次子密钥经过轮函数计算得出
(l, r) = (r, l ^ round_func(r, &self.keys[i]));
}
},
DESMode::Decrypt => {
if i == 15 {
(r, l) = (r, l ^ round_func(r, &self.keys[15 - i]));
} else {
// 和加密一样，但子密钥要反向给出
(l, r) = (r, l ^ round_func(r, &self.keys[15 - i]));
}
}
}
}
// 拼接l和r
let out = ((l as u64) << 32) + r as u64;
// 执行最后的FP置换
*chunk = permute_64(out, &FP);
}
}
}
注意16轮迭代的最后一次中，L和R不应该交换顺序。因为这个Debug了很久。
二进制数据的截取和拼接都是十分自然的。
单元测试
针对轮函数、S盒函数和u64置换函数编写了单元测试：
#[cfg(test)]
mod test {
use super::*;
/// 测试轮函数
#[test]
fn test_round_func() {
let data: u32 = 0b00000000111111111001110111010000;
let truth: u32 = 0b11000111001010101110010110101010;
let key = "111100001011111001100110001010110010101001010010".to_string();
let mut key_bits = [0u8; 48];
for i in 0..48 {
key_bits[i] = match key.chars().nth(i).unwrap() as u8 {
48 => 0,
49 => 1,
_ => panic!("To bit error!"),
};
}
let result = round_func(data, &key_bits);
assert_eq!(result, truth);
}
/// 测试S盒
#[test]
fn test_sbox() {
let data: u64 = 0b100100001001010011111110101001100000111111010000;
let truth: u32 = 0b11101111100001000001100111001010;
let data_str = format!("{:b}", data);
let mut data_vec = vec![];
for i in data_str.chars() {
let temp = match i as u8 {
48 => 0,
49 => 1,
_ => panic!("To bit error!"),
};
data_vec.push(temp);
}
let result = sbox(data_vec);
let mut result_u32: u32 = 0;
for i in result {
result_u32 = result_u32 * 2 + i as u32;
}
assert_eq!(result_u32, truth);
}
/// 测试`permute_64`函数
#[test]
fn test_permute64() {
let data: u64 = 0b111100001011111001100110001010110010101001010010;
let ip_truth: u64 = 10703956940280326392;
let fp_truth = 2354117243453670917;
let r1 = permute_64(data, &IP);
let r2 = permute_64(data, &FP);
assert_eq!(r1, ip_truth);
assert_eq!(r2, fp_truth);
}
}
编写程序时，先编写相对独立的模块，然后编写适当的单元测试，确保其正确工作，然后在此之上构建更复杂的功能。这是我痛苦调试的切身体会。
运行效果
针对字符串的加密/解密
fn des_test_str() {
let key = "desencrypttest";
let mut des_encrypt = Des::from(
key,
"hello world".as_bytes(),
DESMode::Encrypt,
0
);
des_encrypt.deal();
let b = des_encrypt.as_bytes();
print!("密文：");
for i in b {
print!("{} ", i);
}
println!("");
let mut des_decrypt = Des::from(
key,
&des_encrypt.as_bytes(),
DESMode::Decrypt,
"hello world".len(),
);
des_decrypt.deal();
let binding = des_decrypt.as_bytes();
// dbg!(&binding);
let result = std::str::from_utf8(binding.as_slice()).unwrap();
println!("{:?}", result);
}
运行结果：
密文：128 76 37 58 65 6 230 146 96 81 118 14 186 151 151 104
"hello world"
针对文件的加密/解密
实际上所有文件在高级语言中都可以抽象为一个字节流。只要把DES算法封装成接受/输出字节流的形式，就可以处理所有类型的文件。
这里用一张jpeg图片测试。
fn des_test_image() {
let key = "desencrypttest";
let mut file = File::open("test.jpg").unwrap(); // 文件不一定是图片，任何文件都可以
let mut bytes = vec![];
file.read_to_end(&mut bytes).unwrap();
let len = bytes.len();
let mut des_encrypt = Des::from(
key,
&bytes,
DESMode::Encrypt,
0
);
des_encrypt.deal();
let mut des_decrypt = Des::from(
key,
&des_encrypt.as_bytes(),
DESMode::Decrypt,
len,
);
des_decrypt.deal();
let mut out_file = File::create("./out/test.jpg").unwrap();
out_file.write_all(&des_decrypt.as_bytes()).unwrap();
}
上面给出的垃圾实现效率低得可怜。一张不到200KB的图片用了十几秒才完成加/解密过程。
不过代码确实完成了任务😇
使用 Rayon crate 加速计算
Rayon是一个有名的并行计算库。
https://docs.rs/rayon/latest/rayon/
上面的算法实现中，主要的性能瓶颈在于deal函数中的主循环。这个主循环是串行的，对于大文件，循环可能迭代很多次。在我的机器上，这个循环只能用到10%的CPU性能。我们使用Rayon并行化这个循环。
首先添加依赖：
cargo add rayon
然后导入必要的模块：
use rayon::prelude::*;
然后将
pub fn deal(&mut self) {
for chunk in &mut self.data {
// 略
}
}
改成
pub fn deal(&mut self) {
self.data.par_iter_mut().for_each(|chunk| {
// 略
});
}
仅此而已。修改后的代码在我的机器上可以用到70%的CPU性能，加速了许多倍。
