使用HMM进行分类识别（以语音识别为例）
本文内容参考了：
[1] 基于HMM的语音识别系列博客
[2] 从语音识别到股指预测---隐马尔科夫模型(HMM)的一种应用
[3] 知乎问题：HMM 实际应用过程中，如何确定隐含状态数量？
[4] 袁冰清,于淦,周霞.浅说语音识别技术[J].数字通信世界,2020(02):43-44+18.
[5] 陈银燕. 基于HMM和GMM天然地震与人工爆破识别算法研究[D].广西师范大学,2011.
1.HMM和语音识别基本内容
HMM
对于一个HMM模型，其包括：
- 状态集合
- 状态转移概率矩阵
- 发射概率矩阵
- 初始状态（概率向量）
- （部分文章/应用场景会有）结束状态
我们通过种种观测手段，还可以得到一个观测序列。
HMM认为每一个“观测”的背后都蕴含着一个“状态”。“状态”是“真实”的情况，而观测值是对状态进行观测时，观察的结果。对于每种状态，都有一定概率观测成不同的结果，而观测成不同结果的概率储存在发射概率矩阵中。
随着时间的增加（假设观测序列是时序序列），状态在不断转换（包括变成其他状态和变成自己）。由某状态转变为（包括自己的）其他状态的概率，记录在状态转移概率矩阵中。
HMM假设每次状态的转变都仅与其前一个状态相关。
HMM假设观测到的结果仅与对应时间的状态相关。
下述链接包含了对隐状态数确定方法的讨论
知乎问题：HMM 实际应用过程中，如何确定隐含状态数量？
HMM-GMM
相较于HMM中观测是离散值，GMM认为观测数据是连续的，且符合高斯混合模型（GMM）。
高斯混合模型使用多个高斯分布（即正态分布）的组合来描述数据的分布情况。
理论上GMM可以拟合出任意类型的分布，通常用于解决同一集合下的数据包含多个不同的分布的情况（或者是同一类分布但参数不一样，或者是不同类型的分布，比如正态分布和伯努利分布）。
GMM中高斯分量的数量（高斯分布的数量）的确定通常也难以直接推导（陈银燕，2011），很可能需要根据领域知识，或排着试。
语音数据
对于一段语音数据，可以通过多种方法得到一个随着时间变化的多维特征值。根据方法及参数的不同，每个时间点的特征值是一个多维向量。
特征值的维度数对应GMM中高斯分布的维度数。
识别的思路
音频特征提取
首先对音频分帧（即分段），每一帧需要在宏观上足够短（小于一个音素），微观上足够长（至少包含2-3周期）。对于分帧后的波形信息，进行一系列转换，并进行特征提取。假设提取的声学特征维度为12维，则声音在处理后就变成了12行、N列的矩阵。N为总帧数量。
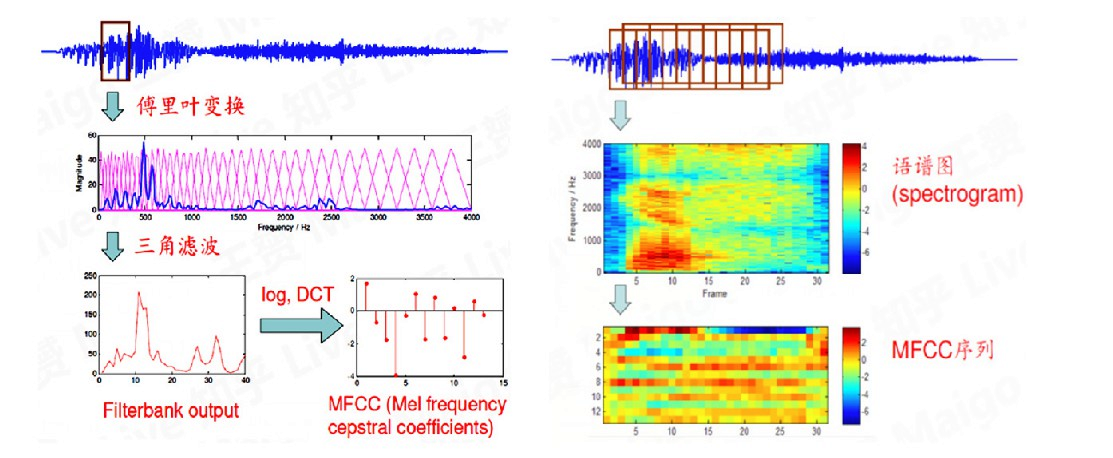
按词切分
假设要对0-9共10个数字进行语音识别。
则对于目前的训练数据（音频），进行模型的训练，得到10个不同的HMM-GMM模型。即对应数字0的模型，应该对标签为0的训练音频数据，得到的后验概率最大。考虑到训练时，Baum–Welch算法可能陷入局部最优，可选取不同初值进行训练，选取score最高的模型。
下式为后验概率的计算，\(M_i\)为对应数字i的模型，\(P(M_i)\)为先验概率，可简单视为等概率。\(P(O|M_i)\)可由前/后向算法算得。
对于待识别的未知语音，用10个模型分别计算后验概率，选择概率最大的作为识别结果。
按音素切分
对于单词进行切分，需要计算大量的模型。而对于音素，则模型数量能够减少许多。音素可以理解为词典中的音标。
下图是一张许多博客都在转载的图。其中，sil表示静音状态。
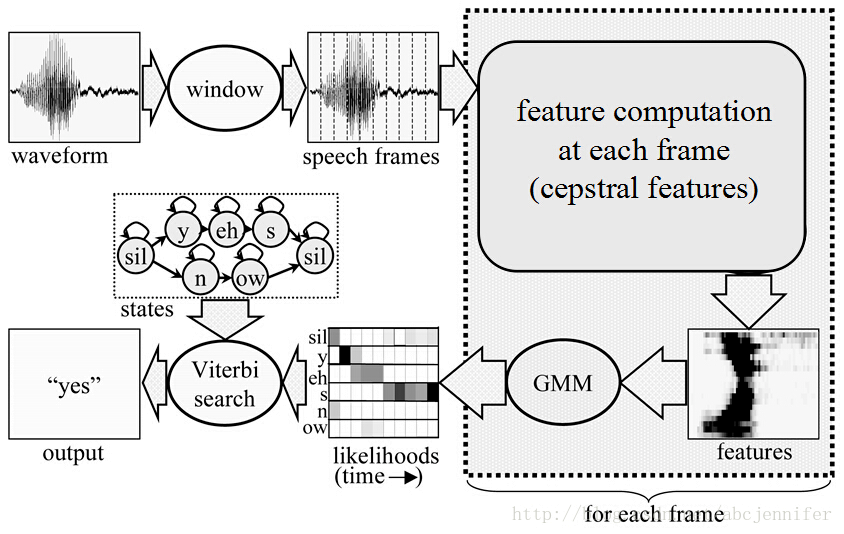
通过对音素建立模型，可以先识别出未知音频的音素序列。通常，对音素建模时，会选取状态数为3。
本文章给出了一种中文语音识别中，确定状态数的方法
张杰,黄志同,王晓兰.语音识别中隐马尔可夫模型状态数的选取原则及研究[J].计算机工程与应用,2000(01):67-69+133.
单词的建模中，可将音素的HMM拼接起来，得到一个大HMM。
上下文相关的音素模型
实际发音中，对于同一个音素，考虑上下文，可能有不同的发音。为了解决这一问题，通常考虑一个音素左右两个音素，建立triphone模型。为了避免遍历全部组合导致的参数量太大，会使用共享模型(Sharing models)和共享状态(Sharing states)两种方法。
共享模型就是把比较类似的triphone聚类在一起，得到的triphone通常叫做Generalized triphone.
共享状态就是更加细粒度的共享，它是把每个triphone的每个状态进行聚类.
实际应用
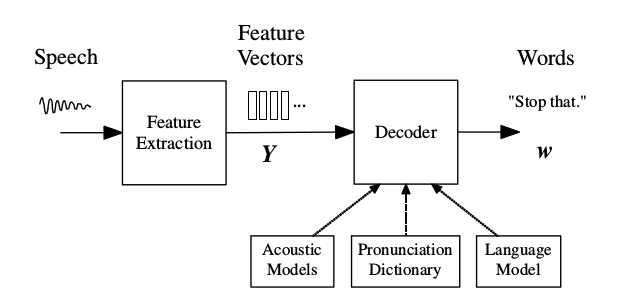
来自麦克风的音频波形被转换成固定大小(比如39维的MFCC)的声学特征向量的序列\(Y_{1:T}=y_1…y_T\)，这个过程叫做特征提取。然后解码器(decoder)试图找到使得后验概率最大最优的词序列\(w_{1:L}=w_1…w_L\)。
因为\(P(w|Y)\)比较难于直接建模，因此我们使用贝叶斯公式，因为分母与w无关，因此可以得到：
\(P(Y|w)\)通过声学模型(Acoustic Model)来确定，而\(P(w)\)由语言模型来确定。
更多应用细节与技巧，可参阅下述博客
李理的博客：基于HMM的语音识别(三)
