图像处理学习笔记-07-小波和多分辨率处理02

一维小波函数

小波级数展开、离散小波变换、连续小波变换分别对应着傅里叶域里面的傅里叶级数展开、离散傅里叶变换、积分傅里叶变换

小波级数展开

对 $f(x) \in L^2$ ，可以在子空间 $V_{j_0}$ 中用尺度函数展开和在子空间 $W_{j_0},W_{j_0 + 1},\cdots$ 中用某些数量的小波函数展开来表示：

f (x) = \sum_{k} c_{j_{0}} (k) φ_{j_{0}, k} (x) + \sum_{j = j_{0}}^{\infty} \sum_{k} d_{j} (k) ψ_{j, k} (x)

$f(x) = \sum_kc_{j_0}(k)\varphi_{j_0,k}(x) + \sum_{j = j_0}^\infty\sum_kd_j(k)\psi_{j,k}(x)$

其中 $j_0$ 是任意的开始尺度， $c_{j_0}(k)$ 称为近似和或尺度系数， $d_j(k)$ 称为细节和或小波系数，如果展开函数形成正交基或紧框架，那么系数可以如下计算：

c_{j_{0}} (k) = ⟨ f (x), φ_{j_{0}, k} (x) ⟩ = \int f (x) φ_{j_{0}, k} (x) d x d_{j} (k) = ⟨ f (x), ψ_{j, k} (x) ⟩ = \int f (x) ψ_{j, k} (x) d x

$c_{j_0}(k) = \left<f(x),\varphi_{j_0,k}(x)\right> = \int f(x)\varphi_{j_0,k}(x)dx \\ d_j(k) = \left<f(x),\psi_{j,k}(x)\right> = \int f(x)\psi_{j,k}(x)dx$

如果展开函数是双正交基的一部分，这些等式中的 $\varphi,\psi$ 需要用其对偶函数来代替

离散小波变换

对应离散函数 $f(n) = f(x_0 + n\Delta x),n = 0,1,2,\cdots,M-1$ ，对连续函数 $f(x)$ 的小波级数展开系数就变为序列 $f(n)$ 的正向离散小波变换DWT系数：

W_{φ} (j_{0}, k) = \frac{1}{\sqrt{M}} \sum_{n} f (n) φ_{j_{0}, k} (n) W_{ψ} (j, k) = \frac{1}{\sqrt{M}} \sum_{n} f (n) ψ_{j, k} (n), j \geq j_{0}

$W_{\varphi}(j_0,k) = \frac{1}{\sqrt M}\sum_nf(n)\varphi_{j_0,k}(n) \\ W_\psi(j,k) = \frac{1}{\sqrt M}\sum_n f(n)\psi_{j,k}(n),j \geq j_0$

在这些等式中， $\varphi_{j_0,k}(n),\psi_{j,k}(n)$ 是基函数 $\varphi_{j_0,k}(x),\psi_{j,k}(x)$ 的取样形式，反向DWT是：

f (n) = \frac{1}{\sqrt{M}} \sum_{k} W_{φ} (j_{0}, k) φ_{j_{0}, k} (n) + \frac{1}{\sqrt{M}} \sum_{j = j_{0}}^{\infty} \sum_{k} W_{ψ} (j, k) ψ_{j, k} (n)

$f(n) = \frac{1}{\sqrt M}\sum_kW_\varphi(j_0,k)\varphi_{j_0,k}(n) + \frac{1}{\sqrt M}\sum_{j = j_0}^\infty\sum_kW_\psi(j,k)\psi_{j,k}(n)$

通常取 $j_0 = 0,M = 2^J$ 为2的幂，在上式中， $n = 0,1,2,\cdots,M-1,j = 0, 1,2,\cdots,J-1,k = 0,1,2,\cdots,2^j - 1$ ，对于哈尔小波，变换中采用的离散尺度和小波函数即基函数和之前 $M \times M$ 的哈尔变换矩阵的行相对应，上面的式子只对正交基和紧框架有效，对于双正交基，需要使用相应的对偶函数

连续小波变换

连续的平方可积函数 $f(x)$ 的连续小波变换与实数值小波 $\psi(x)$ 的关系定义为：

W_{ψ} (s, τ) = \int_{- \infty}^{\infty} f (x) ψ_{s, τ} (x) d x

$W_{\psi}(s,\tau) = \int_{-\infty}^\infty f(x)\psi_{s,\tau}(x)dx$

其中：

ψ_{s, τ} (x) = \frac{1}{\sqrt{s}} ψ (\frac{x - τ}{s})

$\psi_{s,\tau}(x) = \frac{1}{\sqrt{s}}\psi\left(\frac{x - \tau}{s}\right)$

$s,\tau$ 分别是尺度参数和平移参数，给定 $W_\psi(s,\tau)$ ，就可以使用连续小波反变换得到 $f(x)$ :

f (x) = \frac{1}{C_{ψ}} \int_{0}^{\infty} \int_{- \infty}^{\infty} W_{ψ} (s, τ) \frac{ψ_{s, τ} (x)}{s^{2}} d τ d s

$f(x) = \frac{1}{C_\psi}\int_0^\infty\int_{-\infty}^\infty W_\psi(s,\tau)\frac{\psi_{s,\tau}(x)}{s^2}d\tau ds$

其中：

C_{ψ} = \int_{- \infty}^{\infty} \frac{| Ψ (μ) |^{2}}{| μ |} d μ

$C_\psi = \int_{-\infty}^\infty\frac{|\mathbf{\Psi}(\mu)|^2}{|\mu|}d\mu$

$\mathbf{\Psi}(\mu)$ 是 $\psi(x)$ 的傅里叶变换

快速小波变换FWT

类似于子带编码方案，首先考虑多分辨率详细的等式：

φ (x) = \sum_{n} h_{φ} (n) \sqrt{2} φ (2 x - n)

$\varphi(x) = \sum_n h_\varphi (n)\sqrt{2}\varphi(2x - n)$

用 $2^j$ 对 $x$ 尺度化，用 $k$ 对它平移，并令 $m = 2k + n$ ，给出：

\begin{aligned} φ (2^{j} x - k) & = \sum_{k} h_{φ} (n) \sqrt{2} φ (2 (2^{j} x - k) - n) \\ = \sum_{n} h_{φ} (n) \sqrt{2} φ (2^{j + 1} x - 2 k - n) \\ = \sum_{m} h_{φ} (m - 2 k) \sqrt{2} φ (2^{j + 1} x - m) \end{aligned}

$\begin{aligned} \varphi(2^j x - k) &= \sum_kh_\varphi(n)\sqrt{2}\varphi(2(2^jx - k) - n) \\ &= \sum_nh_\varphi(n)\sqrt{2}\varphi(2^{j + 1}x - 2k - n) \\ &= \sum_mh_\varphi(m - 2k)\sqrt{2}\varphi(2^{j + 1}x - m) \end{aligned}$

相似的可以得到小波函数：

ψ (2^{j} x - k) = \sum_{m} h_{ψ} (m - 2 k) \sqrt{2} φ (2^{j + 1} x - m)

$\psi(2^j x - k) = \sum_mh_\psi(m - 2k)\sqrt{2}\varphi(2^{j + 1}x - m)$

有小波定义式如下：

d_{j} (k) = \int f (x) 2^{\frac{j}{2}} ψ (2^{j} x - k) d x

$d_j(k) = \int f(x)2^\frac j2\psi(2^j x - k)dx$

综合起来：

d_{j} (k) = \int f (x) 2^{\frac{j}{2}} [\sum_{m} h_{ψ} (m - 2 k) \sqrt{2} φ (2^{j + 1} x - m)] d x

$d_j(k) = \int f(x)2^\frac j2\left[\sum_mh_\psi(m - 2k)\sqrt{2}\varphi(2^{j + 1}x - m)\right]dx$

交换积分和求和的顺序：

d_{j} (k) = \sum_{m} h_{ψ} (m - 2 k) [\int f (x) 2^{\frac{j + 1}{2}} φ (2^{j + 1} x - m)]

$d_j(k) = \sum_m h_\psi(m - 2k)\left[\int f(x)2^{\frac{j + 1}{2}}\varphi(2^{j + 1}x - m)\right]$

可以看到括号中的量为 $j_0 = j + 1,k = m$ 时的 $c_{j_0}(k)$ ：

d_{j} (k) = \sum_{m} h_{ψ} (m - 2 k) c_{j + 1} (m)

$d_j(k) = \sum_m h_\psi(m - 2k)c_{j + 1}(m)$

也就是尺度 $j$ 的细节系数是尺度 $j + 1$ 的近似函数的系数，类似的可以得到：

c_{j} (k) = \sum_{m} h_{φ} (m - 2 k) c_{j + 1} (m)

$c_j(k) = \sum_mh_\varphi(m - 2k)c_{j + 1}(m)$

当 $f(x)$ 为离散函数的时候，因为小波级数展开的系数 $c_j(k),d_j(k)$ 变为DWT的系数 $W_\varphi(j,k),W_\psi(j,k)$ ，所以：

W_{ψ} (j, k) = \sum_{m} h_{ψ} (m - 2 k) W_{φ} (j + 1, m) W_{φ} (j, k) = \sum_{m} h_{φ} (m - 2 k) W_{φ} (j + 1, m)

$W_\psi(j,k) = \sum_mh_\psi(m - 2k)W_\varphi(j + 1,m) \\ W_\varphi(j,k) = \sum_mh_\varphi(m - 2k)W_\varphi(j + 1, m)$

上式揭示了相邻尺度DWT系数间的关系，DWT的系数 $W_\varphi(j,k),W_\psi(j,k)$ 可以用 $W_\varphi(j + 1, k)$ 分别与顺序倒置尺度和小波向量 $h_\varphi(-n),h_\psi(-n)$ 进行卷积操作，然后对结果进行下采样来计算：

W_{ψ} (j, k) = h_{ψ} (- n) ★ W_{φ} (j + 1, n) |_{n = 2 k, k \geq 0} W_{φ} (j, k) = h_{φ} (- n) ★ W_{φ} (j + 1, n) |_{n = 2 k, k \geq 0}

$W_\psi(j,k) = h_\psi(-n) ★ W_\varphi(j + 1, n)|_{n = 2k,k\geq 0} \\ W_\varphi(j,k) = h_\varphi(-n) ★ W_\varphi(j + 1, n)|_{n = 2k,k\geq 0}$

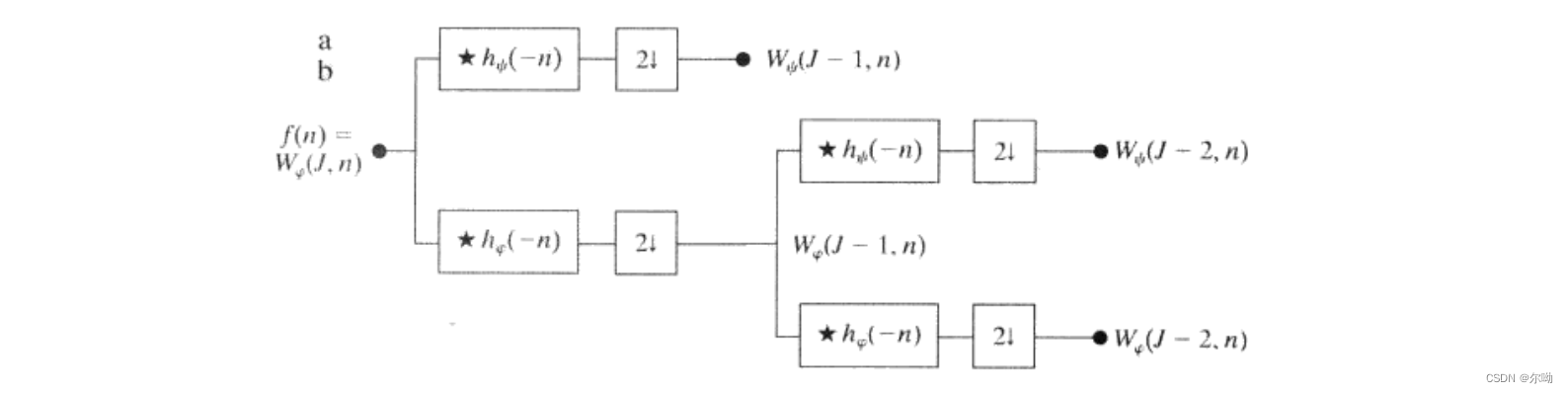
FWT分析滤波器组
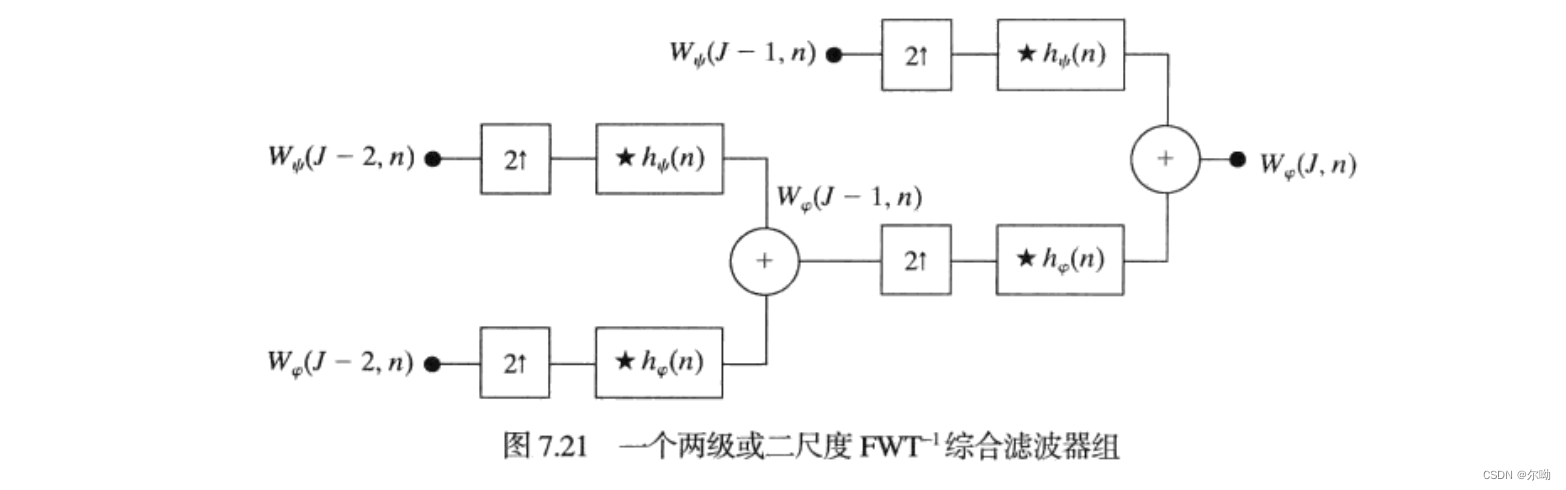
上述过程和子带编码类似， $h_0(n) = h_\varphi(-n),h_1(n) = h_\psi(-n)$ ，得到的 $W_\varphi(j,k),W_\psi(j,k)$ 分别代表低通和高通分量，使用FWT约要求 $O(M\log_2 M)$ 次操作，通常，我们选择 $f(x)$ 的 $2^J$ 个样本，并用 $P$ 个滤波器组在尺度 $J - 1,J - 2,\cdots,J - P$ 处生成一个 $P$ 尺度FWT，首先计算最高尺度即 $J - 1$ 的系数，最后计算最低尺度 $J - P$ 的系数，假设 $f(x)$ 的取样频率合适，那么取样样本时在该取样分辨率下的尺度系数的良好近似，可以作为起始高分辨率尺度系数的输入，类似的，我们可以得到从正变换的结果快速反变换结果，相当于二带宽子带编码的综合过程，由分析过程 $h_0(n) = h_\varphi(-n),h_1(n) = h_\psi(-n)$ ，得到 $g_0(n) = h_0(-n) = h_\varphi(n),g_1(n) = h_1(-n) = h_\psi(n)$ ，反变换 $FWT^{-1}$ 的滤波器组执行下述计算：

W_{φ} (j + 1, k) = h_{φ} (k) ★ W_{φ}^{2 ↑} (j, k) + h_{ψ} (k) ★ W_{ψ}^{2 ↑} (j, k) |_{k \geq 0}

$W_\varphi(j + 1, k) = h_\varphi(k) ★ W_\varphi^{2\uparrow}(j,k) + h_\psi(k) ★ W_\psi^{2\uparrow}(j,k)|_{k \geq 0}$

其中 $W^{2\uparrow}$ 表示基2的上取样，上取样通过插入0使得长度变为原来的两倍来完成的，之后上取样的系数和 $h_\varphi(n),h_\psi(n)$ 进行卷积完成滤波并相加产生较高尺度的近似，本质上创建了 $f(n)$ 的较好近似
一个两级或二尺度FWT反变换综合滤波器组
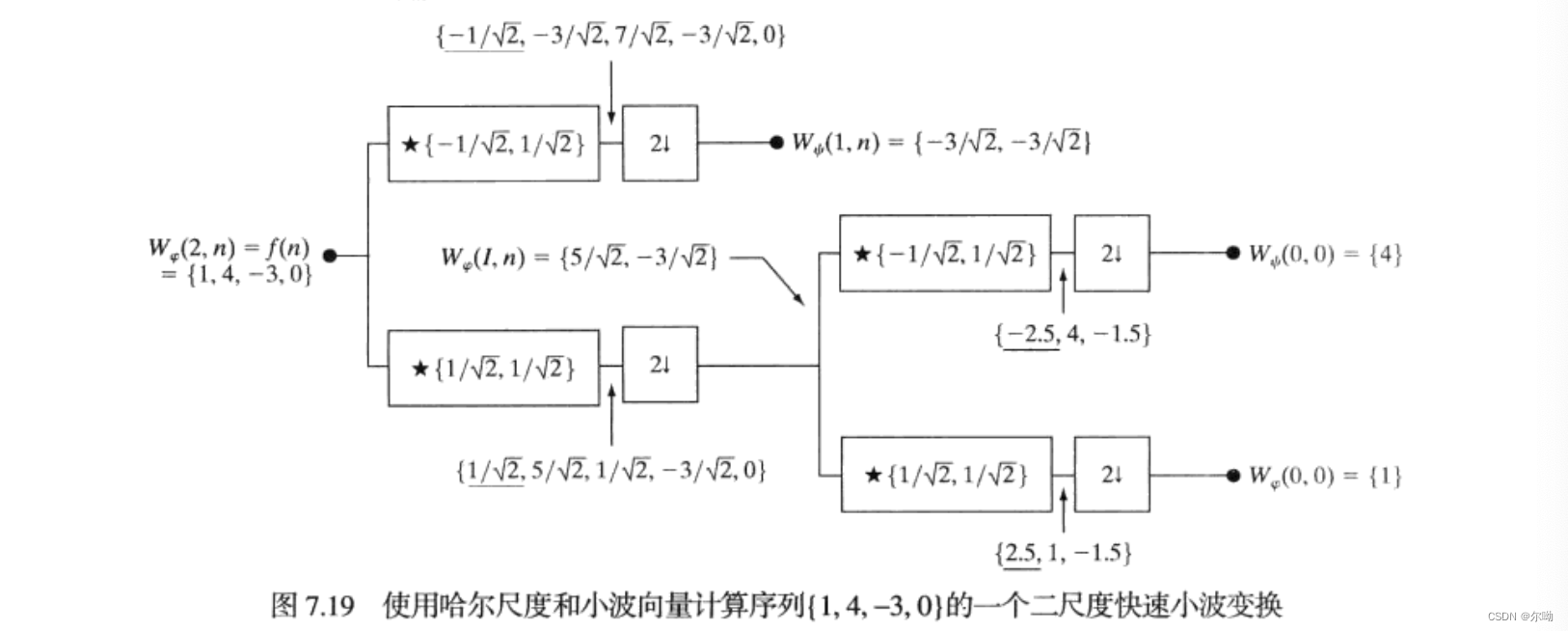
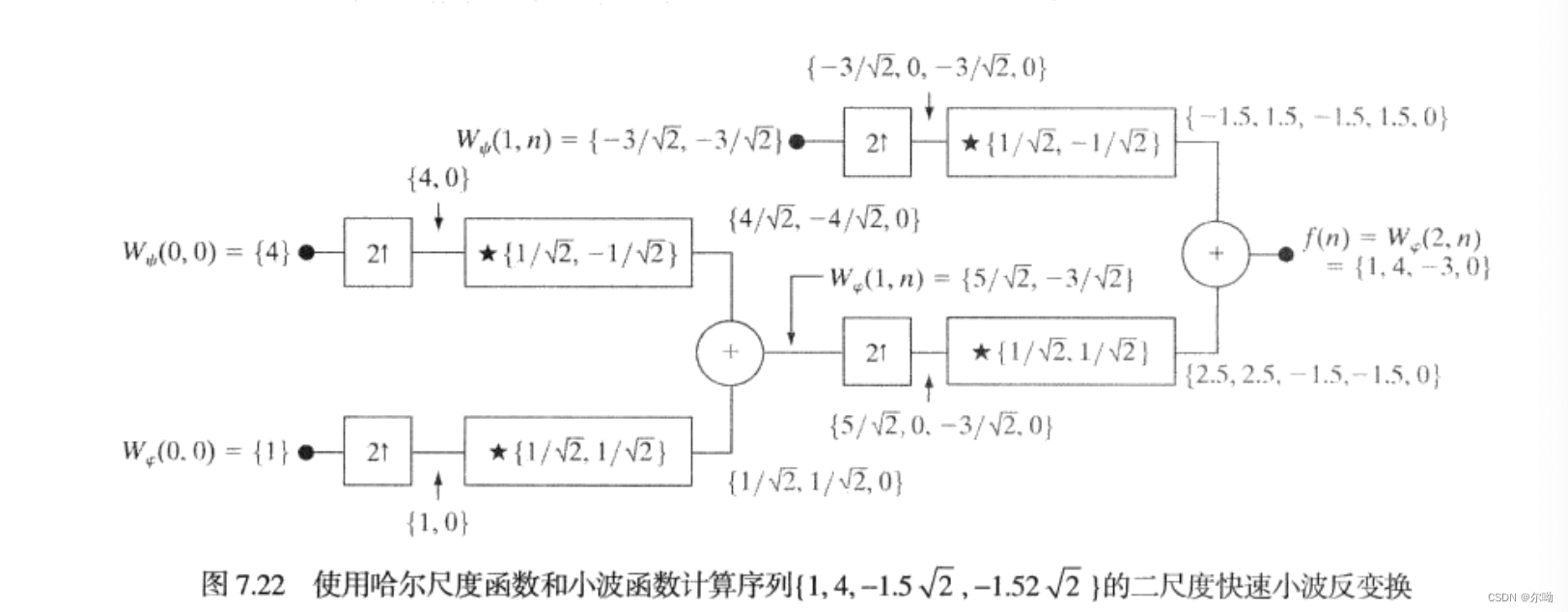
下面是两个示例过程：
小波变换